Finding the Volume of a Solid: Revolving About the \(y\)-Axis

Find the volume \(V\) of the solid generated by revolving the region bounded by the graphs of \(f(x) =x^{2}\) and \(g(x) =12-x\) to the right of \(x=1\) about the \(y\)-axis.

Solution Using the shell method: Figure 33(a) shows the graph of the region to be revolved and a typical rectangle.

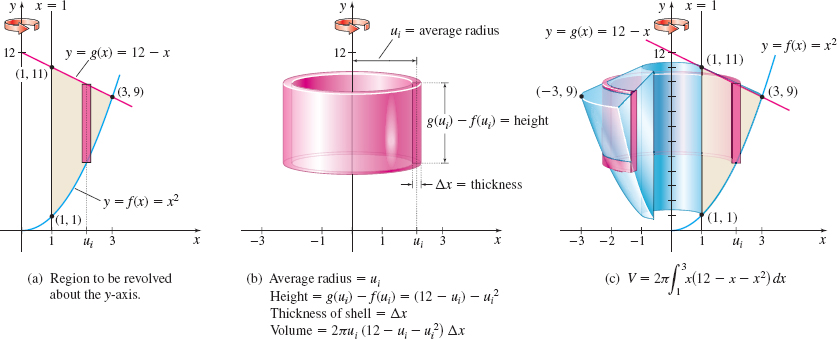
As shown in Figure 33(b), in the shell method, we partition the \(x\)-axis and use vertical shells. A typical shell has height \(h_{i}=g( u_{i}) -f( u_{i}) =(12-u_{i})-u_{i}^{2}=12-u_{i}-u_{i}^{2}\), and volume \(V_{i}=2\pi u_{i}( 12-u_{i}-u_{i}^{2}) \Delta x\). Figure 33(c) shows the solid of revolution. Notice that the integration takes place from \(x=1\) to \(x=3\). The volume \(V\) of the solid of revolution is \begin{eqnarray*}\hskip-1pc V &=&2\pi \int_{1}^{3}x(12-x-x^{2})~{\it dx}=2\pi \int_{1}^{3}( 12x-x^{2}-x^{3}) ~{\it dx}=2\pi \left[ 6x^{2}-\dfrac{x^{3}}{3}-\dfrac{x^{4}}{ 4}\right] _{1}^{3} \\[4pt] &=&2\pi\! \left[ \left( 54-9-\dfrac{81}{4}\right) -\left( 6-\dfrac{1}{3}- \dfrac{1}{4}\right) \right] =\dfrac{116~\pi }{3}\hbox{ cubic units} \end{eqnarray*}

428

Using the washer method: Figure 34 shows the solid of revolution and typical washers.

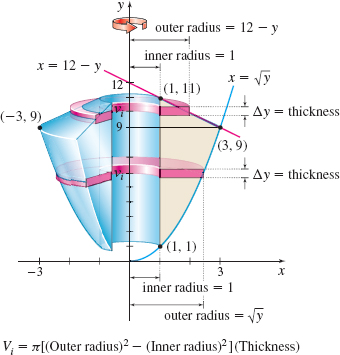
In the washer method, we partition the interval \(\left[ 1,11\right]\) on the \(y\)-axis and use horizontal washers. At \(y=9\), the function on the right changes. The volume of a typical washer in the interval \([1,9]\) is \begin{equation*} V_{i}=\pi \big[ \sqrt{v_{i}}^{2}-1^{2}\big] \Delta y=\pi (v_{i}-1) \Delta y \end{equation*}

The volume of a typical washer in the interval \([9,11]\) is \begin{equation*} V_{i}=\pi \big[ ( 12-v_{i}) ^{2}-1^{2}\big] \Delta y=\pi \big( 143-24v_{i}+v_{i}^{2}\big) \Delta y \end{equation*}

The volume \(V\) of the solid of revolution is \begin{eqnarray*} V &=&\pi \int_{1}^{9}(y-1) ~{\it dy}+\pi \int_{9}^{11} (143-24y+y^{2})~{\it dy}\\[8pt] &=&\pi \left[ \dfrac{y^{2}}{2}-y\right] _{1}^{9}+\pi \left[ 143y-12y^2 +\dfrac{y^{3}}{3} \right] _{9}^{11}\hbox{ } \notag \\[8pt] &=&\pi \left[ \left( \dfrac{81}{2}-9\right) -\left( \dfrac{1}{2}-1\right) \right] +\pi \left( 143\left( 2\right) -(12)(121-81)+\dfrac{11^{3}}{3}-\dfrac{9^{3}}{3}\right)\\[8pt] &=&32\pi +\dfrac{20}{3}\pi =\dfrac{116\,\pi }{3}\hbox{ cubic units} \end{eqnarray*}