Using the Shell Method: Revolving About the \(x\)-Axis

Find the volume \(V\) of the solid generated by revolving the region bounded by the graph of, \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1, a > 0, b > 0\), in the first quadrant, about the \(x\)-axis.

Solution The equation \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\) defines an ellipse. The intercepts of its graph are \((a,0), (0,b), (-a,0)\), and \((0,-b)\). The region to be revolved is the shaded region in the first quadrant shown in Figure 36(a).

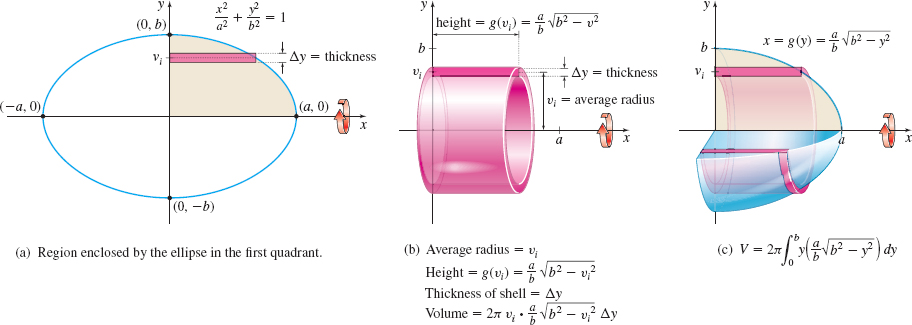
In the shell method, when the region is revolved about the \(x\)-axis, we partition the \(y\)-axis and use horizontal shells. A revolution about the \(x\)-axis requires integration with respect to \(y\), so we express the equation of the ellipse as \[ x=g(y)=\dfrac{a}{b}\sqrt{~b^{2}-y^{2}} \]

430

The volume of a typical shell is \[ V_{i}=2\pi\ \hbox{(Average radius)(Height)(Thickness)} = 2\pi v_{i}g(v_{i})\Delta y \]

See Figure 36(b).

Figure 36(c) shows the solid of revolution. The volume \(V\) of the solid of revolution is \begin{eqnarray*} V &=&2\pi \int_{0}^{b}y~g(y)~{\it dy}=2\pi \int_{0}^{b}y\left( \dfrac{a}{b}\sqrt{ b^{2}-y^{2}}\right) {\it dy} \underset{\underset{\underset{\color{#0066A7}{\hbox{then \({du}={-2y}{ dy}\)}}}{\color{#0066A7}{\hbox{Let \(u=b^2-y^2\);}}}}{\color{#0066A7}{\uparrow }}} {=} 2\pi \dfrac{a}{b}\left( -\dfrac{1}{2}\right) \int_{b^{2}}^{0}\sqrt{u}\ {\it du} \\[-9pt] &=&\dfrac{\pi a}{b}\int_{0}^{b^{2}}u^{1/2}~{\it du}=\dfrac{\pi a}{b}\left[ \dfrac{ u^{3/2}}{\dfrac{3}{2}}\right] _{0}^{b^{2}}=\dfrac{2\pi a}{3b}( b^{3}) =\dfrac{2\pi ab^{2}}{3}\hbox{ cubic units} \end{eqnarray*}