Using the Slicing Method to Find the Volume of a Solid

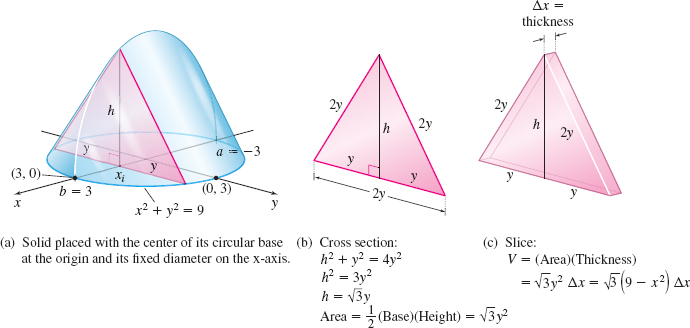
A solid has a circular base of radius \(3\) units. Find the volume \(V\) of the solid if every plane cross section that is perpendicular to a fixed diameter is an equilateral triangle.

Solution Position the circular base so that its center is at the origin, and the fixed diameter is along the \(x\)-axis. See Figure 41(a). Then the equation of the circular base is \(x^{2}+y^{2}=9\). Each cross section of the solid is an equilateral triangle with sides \(= 2y,\) height \( h,\) and area \(A=\sqrt{3}y^{2}\). See Figure 41(b). Since \(y^{2}=9-x^{2},\) the volume \(V_i\) of a typical slice is \[ V_{i}=\hbox{(Area of the cross section)(Thickness)}=A(x_{i})~\Delta x=\sqrt{3 }\left( 9-x_{i}^{2}\right) \Delta x \] as shown in Figure 41(c).

435

The volume \(V\) of the solid is \begin{eqnarray*} V&=&\int_{a}^{b}A(x)~{\it dx}=\int_{-3}^{3}\sqrt{3}(9-x^{2})~{\it dx} \underset{\underset{\underset{\color{#0066A7}{\hbox{an even function.}}}{\color{#0066A7}{\hbox{The integrand is}}}} {\color{#0066A7}{\uparrow }}} {=}2\sqrt{3}\int_{0}^{3}(9-x^{2})~{\it dx}=2\sqrt{3}\left[ 9x-\frac{ x^{3}}{3}\right] _{0}^{3}\\[-10pt] &=&36\sqrt{3}\hbox{ cubic units} \end{eqnarray*}