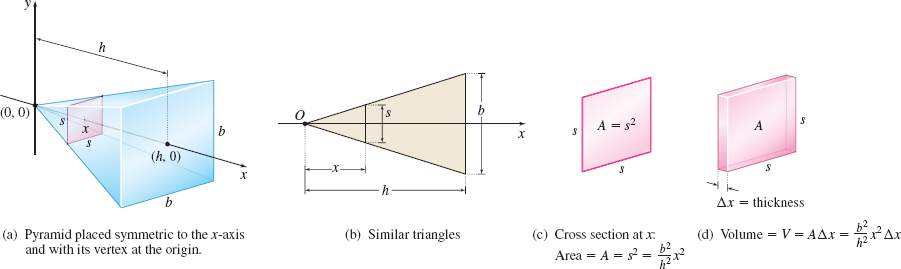
Using the Slicing Method to Find the Volume of a Pyramid

Find the volume \(V\) of a pyramid of height \(h\) with a square base, each side of length \(b\).

Solution We position the pyramid with its vertex at the origin and its axis along the positive \(x\)-axis. Then the area \(A\) of a typical cross section at \(x\) is a square. Let \(s\) denote the length of the side of the square at \(x\). See Figure 42(a). We form two triangles: one with height \(x\) and side \(s\), the other with height \(h\) and side \(b.\) These triangles are similar (AAA), as shown in Figure 42(b). Then we have \begin{equation*} \dfrac{x}{s}=\dfrac{h}{b}\qquad\hbox{ or }\qquad s =\dfrac{b}{h}x \end{equation*}

436

So, \(s\) is a function of \(x\), and the area \(A\) of a typical cross section is \(A=s^{2}=\dfrac{b^{2}}{h^{2}}x^{2}\). See Figure 42(c). The volume \(V\) of a typical cross section is \(V=\dfrac{ b^{2}}{h^{2}}x^{2}\Delta x\). See Figure 42(d).

Since \(A\) is a continuous function of \( x\), where the slice occurred, we have \begin{equation*} V=\int_{0}^{h}A(x) \,{\it dx}=\displaystyle \int_{0}^{h}\dfrac{b^{2}}{h^{2}} x^{2}{\it dx}= \frac{b^{2}}{h^{2}}\int_{0}^{h}x^{2}{\it dx}=\frac{b^{2}}{h^{2}} \left[ \frac{x^{3}}{3} \right] _{0}^{h}=\frac{1}{3}b^{2}h\hbox{ cubic units} \end{equation*}