Integrating a Rational Function Whose Denominator Contains a Repeated Irreducible Quadratic Factor

Find \(\int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}\,dx\).

Solution  The denominator is a repeated, irreducible quadratic, so the decomposition of \(\dfrac{x^{3}+1}{(x^{2}+4)^{2}}\) is \[ \dfrac{x^{3}+1}{(x^{2}+4)^{2}}=\dfrac{Ax+B}{x^{2}+4}+\dfrac{Cx+D}{(x^{2}+4)^{2}} \]

505

Clearing fractions and combining terms give \[ \begin{eqnarray*} x^{3}+1 &=& (Ax+B) (x^{2}+4) +Cx+D \\[3pt] x^{3}+1 &=& Ax^{3}+Bx^{2}+(4A+C)x+4B+D \end{eqnarray*} \]

Equating coefficients, we get \[ \begin{equation*} \begin{array}{rl@{\qquad}rrr} A=1 \quad B=0\quad 4A+C &= 0 & 4B+D &= 1 \\[3pt] C &=-4 & D &=1 \end{array} \end{equation*} \]

Then \[ \begin{equation*} \dfrac{x^{3}+1}{(x^{2}+4)^{2}}=\dfrac{x}{x^{2}+4}+\dfrac{-4x+1}{(x^{2}+4)^{2}} \end{equation*} \]

and \[ \begin{eqnarray*} \int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}dx &=& \int \dfrac{x}{x^{2}+4}dx+\int \dfrac{ -4x+1}{(x^{2}+4)^{2}}dx \nonumber\\[5pt] & =& \int \dfrac{x}{x^{2}+4}dx-4\int \dfrac{x}{(x^{2}+4)^{2} }dx+\int \dfrac{dx}{(x^{2}+4)^{2}}\tag{3} \end{eqnarray*} \]

In the first two integrals on the right in (3), we use the substitution \(u=x^{2}+4\) , \(x \geq 0.\) Then \(du=2x\,dx\), and

\(\int \dfrac{x}{x^{2}+4}dx = \dfrac{1}{2}\int \dfrac{du}{u}=\dfrac{1}{2}\ln \vert u \vert =\dfrac{1}{2}\ln (x^{2}+4) \tag{4}\)

\(-4\int \dfrac{x}{(x^{2}+4)^{2}}dx = -2\int \dfrac{\,du}{u^{2}}=\dfrac{2}{u}= \dfrac{2}{x^{2}+4}\tag{5}\)

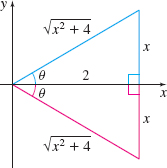
In the third integral on the right in (3), we use the trigonometric substitution \( x=2\tan \theta \), \(-\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi }{2}.\) Then \( dx=2\sec ^{2} \theta \,d\theta \), and \[ \begin{eqnarray*} \int \dfrac{dx}{(x^{2}+4)^{2}} &=& \int \dfrac{2\sec ^{2} \theta \,d\theta }{ \left( 4\tan ^{2}\theta +4\right) ^{2}}=\dfrac{2}{16}\int \dfrac{\sec ^{2} \theta \,d\theta }{( \sec ^{2} \theta) ^{2}}=\dfrac{1}{8}\int \cos ^{2}\theta \,d\theta \\[7pt] &=& \dfrac{1}{8}\int \dfrac{1+\cos (2\theta) }{2}d\theta \\[7pt] &=& \dfrac{1}{16}\left[ \theta +\dfrac{1}{2}\sin (2\theta ) \right] =\dfrac{1}{16}(\theta +\sin \theta \cos \theta ) \end{eqnarray*} \]

To express the solution in terms of \(x\), either use the triangles in Figure 10 or use trigonometric identities as follows: \[ \begin{equation*} \sin \theta \cos \theta =\dfrac{\sin \theta }{\cos \theta }\cdot \cos ^{2}\theta =\dfrac{\tan \theta }{\sec ^{2} \theta }=\dfrac{\tan \theta }{\tan ^{2}\theta +1}=\dfrac{\dfrac{x}{2}}{\dfrac{x^{2}}{4}+1}=\dfrac{2x}{x^{2}+4} \end{equation*} \]

Then \[ \begin{eqnarray*} \int \dfrac{dx}{(x^{2}+4)^{2}} &=& \dfrac{1}{16}(\theta +\sin \theta \cos \theta )\underset{\underset{\color{#0066A7}{\hbox{\(x=2\tan \theta{;} \theta =\tan^{-1}\dfrac{x}{2}\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{1}{16}\left( \tan ^{-1}\dfrac{x}{2}+\dfrac{2x}{x^{2}+4}\right)\tag{6} \end{eqnarray*} \]

Now use the results of (3), (4), (5), and (6): \[ \int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}dx=\dfrac{1}{2}\ln (x^{2}+4)+\dfrac{2}{ x^{2}+4}+\dfrac{1}{16}\tan ^{-1}\dfrac{x}{2}+\dfrac{x}{8(x^{2}+4)}+C_{1} \]