Approximating \(\displaystyle\int_{0}^{\pi }\sin x\, dx\) Using the Trapezoidal Rule

1. Use the Trapezoidal Rule with \(n=4\) and \(n=6\) to approximate \( \int_{0}^{\pi }\sin x\,dx\), rounded to three decimal places.
2. Compare each approximation to the exact value of \(\int_{0}^{\pi }\sin xdx\).

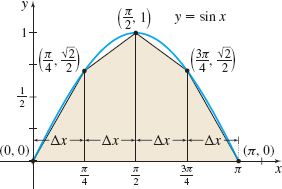
Solution  (a) We partition the interval \([0,\pi] \) into four subintervals, each of width \(\Delta x=\dfrac{\pi -0}{4}=\dfrac{\pi }{4}.\) \[ \left[ 0,\dfrac{\pi }{4}\right] \qquad \left[ \dfrac{\pi }{4},\dfrac{ \pi }{2}\right]\hbox{} \qquad \left[ \dfrac{\pi }{2},\dfrac{3\pi }{4}\right] \hbox{}\qquad \left[\dfrac{3\pi }{4},\pi \right] \]

510

The values of \(f( x) =\sin x\) corresponding to each endpoint are \[ f(0) =0 \!\qquad f\!\left( \dfrac{\pi }{4} \right) =\dfrac{\sqrt{2}}{2}\!\qquad f\!\left( \dfrac{\pi }{2} \right) =1\!\qquad f\!\left( \dfrac{3\pi }{4}\right) = \dfrac{\sqrt{2}}{2}\!\qquad f (\pi) =0 \]

See Figure 14. Now we use the Trapezoidal Rule: \[ \begin{eqnarray*} \int_{0}^{\pi }\sin x\,dx &\approx &\dfrac{\pi -0}{2\cdot 4}\,\left[ \sin (0)+2\,\sin \left( \dfrac{\pi }{4}\right) +2\,\sin \left( \dfrac{\pi }{2} \right) +2\,\sin \left( \dfrac{3\pi }{4}\right) +\sin (\pi )\right] \\[6pt] &=&\dfrac{\pi }{8}\,\left[ 0+2\left( \dfrac{\sqrt{2}}{2}\right) +2\left( 1\right) +2\left( \dfrac{\sqrt{2}}{2}\right) +0\right] =\dfrac{\pi }{8} \big( 2+2\sqrt{2}\big) \\[6pt] &=& \dfrac{\pi }{4}\big( 1+\sqrt{2}\big) \approx 1.896 \end{eqnarray*} \]

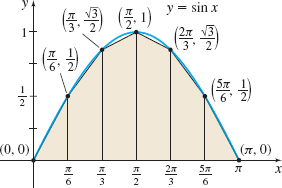
To approximate \(\int_{0}^{\pi }\sin x\,dx\) using six subintervals, we partition \([0,\pi] \) into six subintervals, each of width \( \Delta x=\dfrac{\pi -0}{6}=\dfrac{\pi }{6},\) namely, \[ \left[ 0,\dfrac{\pi }{6}\right]\! \qquad \left[ \dfrac{\pi }{6},\dfrac{ \pi }{3}\right]\!\qquad \left[ \dfrac{\pi }{3},\dfrac{\pi }{2}\right]\! \qquad \left[ \dfrac{\pi }{2},\dfrac{2\pi }{3}\right]\!\qquad \left[\dfrac{2\pi }{3},\dfrac{5\pi }{6}\right]\! \qquad \left[ \dfrac{ 5\pi }{6},\pi \right] \]

See Figure 15. Then we use the Trapezoidal Rule. \[ \begin{eqnarray*} \int_{0}^{\pi }\sin x\,dx &\approx & \dfrac{\pi }{2\cdot 6}\left[ 0+2\cdot \dfrac{1}{2}+2\cdot \dfrac{\sqrt{3}}{2}+2\cdot 1+2\cdot \dfrac{\sqrt{3}}{2} +2\cdot \dfrac{1}{2}+0\right] \\[5pt] &=&\dfrac{\pi }{12}(4+2\sqrt{3}) = \dfrac{\pi }{6}(2+\sqrt{3}) \approx 1.954 \end{eqnarray*} \]

(b) The exact value of the integral is \[ \int_{0}^{\pi }\sin x \, dx = \big[-\cos x\big] _{0}^{\pi }=-\cos \pi +\cos 0=1+1=2 \]

The approximation using the Trapezoidal Rule with four subintervals underestimates the integral by \(0.104.\) The approximation using six subintervals underestimates the integral by \(0.046.\) Notice that the approximation using six subintervals is more accurate than the approximation using four subintervals.