Find the volume of the solid of revolution, called Gabriel’s Horn, that is generated by revolving the region bounded by the graph of $y=\frac{1}{x}$ and the $x$-axis to the right of $1$ about the $x$-axis. Use the disk method.

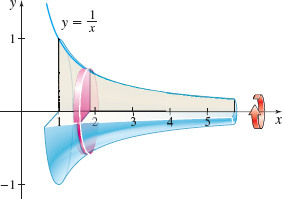
Figure 24 Gabriel’s Horn

Solution Figure 24 illustrates the region being revolved and the solid of revolution that it generates. Using the disk method, the volume $V$ is $$\begin{eqnarray*} V=\pi \int_{1}^{\infty }\!\!\left( \frac{1}{x}\right) ^{2} dx\hbox{:}\quad \pi \lim\limits_{b\,\rightarrow \,\infty }\int_{1}^{b}\!\!\frac{1}{x^{2}} \,dx&=&\pi \lim\limits_{b\rightarrow \infty }\left[ -\frac{1}{x}\right] _{1}^{b}\\[6pt] &=&\pi \lim\limits_{b\rightarrow \,\infty }\left( -\frac{1}{b} + 1\right) = \pi \end{eqnarray*}$$

The volume of the solid of revolution is $\pi$ cubic units.