Determine if the area under the graph of $y=\dfrac{1}{\sqrt{x}}$ from $0$ to $4$ is defined.

Solution Figure 27 shows the area under the graph of $y=\dfrac{1}{ \sqrt{x}}$ from $0$ to $4.$ The area is given by $\int_{0}^{4}\dfrac{1}{ \sqrt{x}}dx.$ Since the integrand $f(x)=\dfrac{1}{\sqrt{x}}$ is continuous on (0, 4] but is not defined at 0, $\int_{0}^{4}\dfrac{1}{ \sqrt{x}}~dx$ is an improper integral. $$\begin{eqnarray*} \int_{0}^{4}\dfrac{1}{\sqrt{x}}\,dx:\quad \lim_{t\,\rightarrow \,0^{+}}\int_{t}^{4}\dfrac{1}{\sqrt{x}}\,dx &=& \lim_{t\,\rightarrow \,0^{+}}\int_{t}^{4}x^{-1/2}dx=\lim_{t\,\rightarrow \,0^{{ +} }}\left[ \dfrac{x^{1/2}}{\dfrac{1}{2}}\right] _{t}^{4}\\[5pt] &=& \lim_{t\,\rightarrow \,0^{+}}\big( 2\cdot 2-2\sqrt{t}\,\big) =4-2\lim_{t\,\rightarrow \,0^{+}}\sqrt{t}=4 \end{eqnarray*}$$ So, $\int_{0}^{4}\dfrac{1}{\sqrt{ x}}\,dx$ converges, and the area under the graph of $y=\dfrac{1}{\sqrt{x}}$ from $0$ to $4$ is defined and equals $4$.

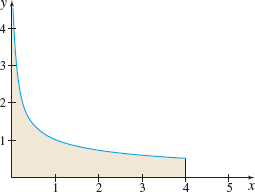
Figure 27 $y=\dfrac{1}{\sqrt{x}}$, $0 \lt x \le 4$.