Find the area under the graph of $f( x) =x\ln x$ from $1$ to $2.$

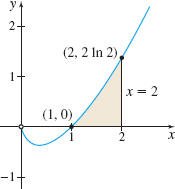
Figure 1 $f(x)=x\ln x$

Solution See Figure 1 for the graph of $f( x) =x\ln x$. The area $A$ under the graph of $f$ from $1$ to $2$ is $A=\int_{1}^{2}x\ln x\,dx.$ We use the integration by parts formula with $$\begin{equation*} u=\ln x\qquad \hbox{and}\qquad dv=x\,dx \end{equation*}$$

Then $$\begin{equation*} du=\frac{1}{x} dx\qquad \hbox{and}\qquad v=\int x dx=\frac{x^{2}}{2} \end{equation*}$$

and $$\begin{eqnarray*} A=\int_{1}^{2}x\ln x\,dx&=&\left[ \frac{x^{2}}{2}\ln x\right] _{1}^{2}-\int_{1}^{2}\frac{x^{2}}{2}\left( \frac{1}{x} dx\right) =2\ln 2-\dfrac{1}{2}\int_{1}^{2}x\,dx\\[5pt] &=&2\ln 2- \dfrac{1}{2}\left[ \frac{x^{2}}{2}\right] _{1}^{2}=2\ln 2-\dfrac{3}{4} \end{eqnarray*}$$