Finding the Average Value of a Function

Find the average value \(\bar{y}\) of the function \(f( x) =\cos ^{4}x\) over the closed interval \([0,\pi]\).

Solution The average value \(\bar{y}\) of a function \(f\) over \([a,b]\) is \(\bar{y}=\dfrac{1}{b-a}\int_{a}^{b}f(x)\,dx.\)

For \(f( x) =\cos ^{4}x\) on \([0,\pi]\), we hav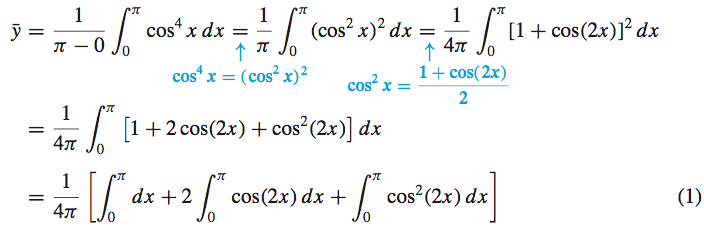e

Now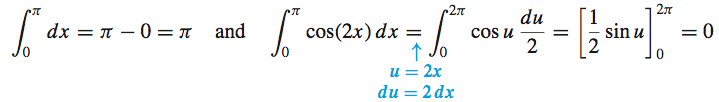

To find \(\int_{0}^{\pi }\cos ^{2}(2x)\, dx,\) we use the identity \( \cos ^{2}\theta =\dfrac{1+\cos (2\theta )}{2}\) again to write \(\cos ^{2}(2x) =\dfrac{1+\cos (4x) }{2}\). Then \[ \begin{eqnarray*} \int_{0}^{\pi }\cos ^{2}(2x) \,dx &=&\int_{0}^{\pi }\dfrac{ 1+\cos (4x) }{2}\,dx=\dfrac{1}{2}\left[ \int_{0}^{\pi }dx+\int_{0}^{\pi }\cos ( 4x) \,dx\right]\\[7pt] &=& \dfrac{1}{2}\left[ \pi +\int_{0}^{4\pi }\cos u\,\dfrac{du}{4}\right] \qquad {\color{#0066A7}{\hbox{\(u=4x\); \(du=4\,dx\)}}} \end{eqnarray*} \]

So, from (1), \[ \bar{y}=\dfrac{1}{4\pi }\left[ \pi +0+\dfrac{\pi }{2}\right] =\dfrac{3}{8} \]