Find $\int \dfrac{dx}{x^{2}\sqrt{4-x^{2}}}$.

Solution The integrand contains the square root $\sqrt{4-x^{2}}$ that is of the form $\sqrt{a^{2}-x^{2}}$, where $a=2$. We use the substitution $x=2\sin \theta$, $-\dfrac{\pi }{2} \lt\theta \lt\dfrac{\pi }{2}$. Then $dx=2\cos \theta \,d\theta$. Since $$\begin{eqnarray*} {\sqrt{4-x^{2}}} \underset{\underset{\color{#0066A7}{\hbox{\(x=2\sin \theta\)}}}{\color{#0066A7}{\uparrow }}} {=} {\sqrt{4-4\sin ^{2}\theta }}=2{\sqrt{1-\sin ^{2}\theta }}=2{\sqrt{\cos ^{2}\theta }} \underset{\underset{\color{#0066A7}{\hbox{\(\text {cos}~\theta \gt 0~\text {since} -\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2}\)}}}{\color{#0066A7}{\uparrow}}}{=}2\cos \theta \end{eqnarray*}$$

we have $$\int\! \frac{dx}{x^{2}\sqrt{4-x^{2}}}=\int\! \frac{2\cos \theta \,d\theta }{ (4\sin ^{2}\theta )(2\cos \theta )}=\int\! \dfrac{d\theta }{4\sin ^{2}\theta }= \frac{1}{4}\int \csc ^{2}\theta \,d\theta =-\frac{1}{4}\cot \theta +C$$

The original integral is a function of $x$, but the solution above is a function of $\theta$. To express $\cot \theta$ in terms of $x$, refer to the right triangles drawn in Figure 4.

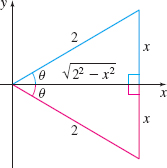
Figure 4 $\sin \theta =\dfrac{x}{2}$, $-\dfrac {\pi}{2} \lt \theta \lt \dfrac {\pi}{2}$

Using the Pythagorean Theorem, the third side of each triangle is $\sqrt{ 2^{2}-x^{2}}=\sqrt{4-x^{2}}$. So, $$\cot \theta =\dfrac{\sqrt{4-x^{2}}}{x} \qquad -\dfrac{\pi }{2} \lt\theta \lt \dfrac{\pi }{2}$$

Then $$\int \dfrac{dx}{x^{2}\sqrt{4-x^{2}}}=-\frac{1}{4}\cot \theta +C=-\frac{1}{4}\frac{\sqrt{4-x^{2}}}{x}+C=-\frac{\sqrt{4-x^{2}}}{4x}+C$$