Finding the Area Enclosed by an Ellipse

Find the area \(A\) enclosed by the ellipse \(\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}=1.\)

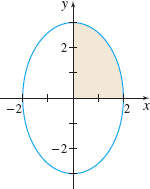
Solution Figure 8 illustrates the ellipse. Since the ellipse is symmetric with respect to both the \(x\)-axis and the \(y\)-axis, the total area \(A\) of the ellipse is four times the shaded area in the first quadrant, where \(0 \le x \le 2\) and \(0 \le y \le 3.\)

We begin by expressing \(y\) as a function of \(x.\) \[ \begin{eqnarray*} \frac{x^{2}}{4}+\frac{y^{2}}{9} &=&1 \\[4.5pt] \frac{y^{2}}{9} &=&1-\frac{x^{2}}{4}=\frac{4-x^{2}}{4} \\[4.5pt] y^{2} &=&\dfrac{9}{4}( 4-x^{2}) \\[4.5pt] y &=&\dfrac{3}{2}\sqrt{4-x^{2}}\qquad {\color{#0066A7}{\hbox{\(y \ge 0\)}}} \end{eqnarray*} \]

So, the area \(A\) of the ellipse is four times the area under the graph of \(y=\dfrac{3}{2}\sqrt{4-x^{2}},\) \(0 \le x \le 2.\) That is, \[ A=4 \int_{0}^{2}\dfrac{3}{2}\sqrt{4-x^{2}}\,dx =6\int_{0}^{2}\sqrt{4-x^{2}}\,dx \]

Since the integrand contains a square root of the form \(\sqrt{a^{2}-x^{2}}\) with \(a=2,\) we use the substitution \(x=2\sin \theta\), \(-\frac{\pi}{2} \le \theta \le \frac{\pi }{2}\). Then \(dx=2\cos \theta \,d\theta\). The new limits of integration are:

When \(x=0\), \(2\sin \theta =0\), so \(\theta =0\).

When \(x=2\), \(2\sin \theta =2\), so \(\sin \theta =1\) and \(\theta =\dfrac{\pi }{2}\).

Then \[ \begin{eqnarray*} A&=&6\int_{0}^{2}\sqrt{4-x^{2}}\,dx=6\int_{0}^{\pi /2}\sqrt{4-4\sin^{2}\theta }\cdot 2\cos \theta \,d\theta\\ &=&6\int_{0}^{\pi /2}2\sqrt{1-\sin^{2}\theta }\cdot 2\cos \theta \,d\theta = 24\int_{0}^{\pi /2}\sqrt{\cos ^{2}\theta }\cdot \cos \theta \,d\theta\nonumber \\ &\underset{\underset{\color{#0066A7}{\hbox{\(\cos \theta \ge 0\)}}}{\color{#0066A7}{\uparrow }}}{=}&24\int_{0}^{\pi /2}\cos^{2}\theta \,d\theta \underset{\underset{\color{#0066A7}{\hbox{\(\cos^{2}\theta =\frac{1+\cos (2\theta )}{2}\)}}}{\color{#0066A7}{\uparrow }}}{=} \frac{24}{2}\int_{0}^{\pi /2}\left[1+\cos (2\theta ) \right] \,d\theta \nonumber \\ & =&12\left[ \theta +\frac{1}{2}\sin (2\theta ) \right]_{0}^{\pi /2}=12\left( \frac{\pi }{2}+0\right) =6\pi \end{eqnarray*} \]

The area of the ellipse is \(6\pi\) square units.