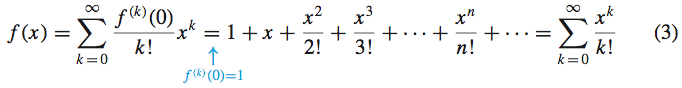Expressing a Function as a Maclaurin Series

Assuming that \(f(x)=e^{x}\) can be represented by a power series in \(x\), find its Maclaurin series.

Solution To express a function \(f\) as a Maclaurin series, we begin by evaluating \(f\) and its derivatives at \(0\). \[ \begin{array}{rl@{\qquad}rll} f(x) & =e^{x} & f(0) &=1 \\ f^{\prime} (x)& =e^{x} & f^{\prime} (0) & =1 \\ f^{\prime \prime} (x) & =e^{x} & f^{\prime \prime} (0) &=1 \\ & \vdots & & \vdots \end{array} \]

Then we use the definition of a Maclaurin series.