Graphing a Polar Equation (Rose); Finding Parametric Equations

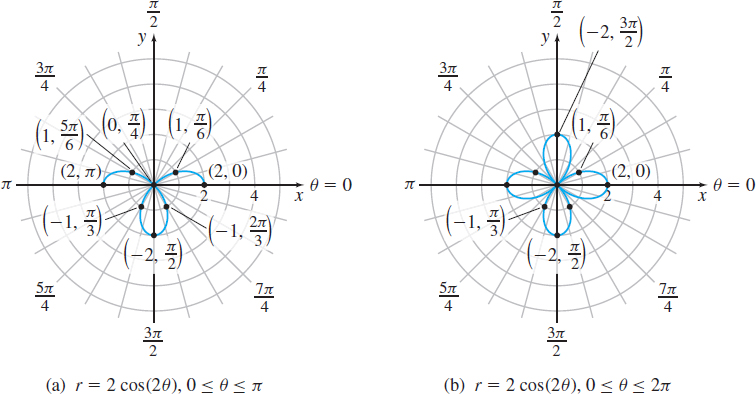
(a) Graph the polar equation \(r=2 \ \cos ( 2\theta ) ,\) \(0\leq \theta \leq 2\pi\).

(b) Find parametric equations for \(r=2 \ \cos ( 2\theta )\).

Graphs of polar equations of the form \(r=a \ \cos (n\theta )\) or \(r =a \ \sin ( n\theta ),\;a>0,\;n\) an integer, are called roses. If \(n\) is an even integer, the rose has \(2n\) petals and passes through the pole \(4n\) times. If \(n\) is an odd integer, the rose has \(n\) petals and passes through the pole \(2n\) times.

Solution (a) The polar equation \(r=2 \ \cos ( 2\theta )\) contains \(\cos ( 2\theta )\), which has the period \(\pi\). So, we construct Table 5 using common values of \(\theta\) that range from \(0\) to \(2\pi\), noting that the values for \(\pi \leq \theta \leq 2\pi\) repeat the values for \(0\leq \theta \leq \pi .\) Then we plot the points \(( r,\theta)\) and trace out the graph. Figure 46(a) on page 674 shows the graph from the point \(( 2,0)\) to the point \(( 2, \ \pi).\) Figure 46(b) completes the graph from the point \(( 2, \ \pi)\) to the point \(( 2, \ 2\pi )\).

TABLE 5
\(\theta\) \(r=2 \ \cos ( 2\theta )\) \(( r,\theta )\)
\(0\) \(2(1) =2\) \(( 2,0)\)
\(\dfrac{\pi }{6}\) \(2\left( \dfrac{1}{2}\right) =1\) \(\left( 1,\dfrac{\pi }{6}\right)\)
\(\dfrac{\pi }{4}\) \(2\left( 0\right) =0\) \(\left( 0,\dfrac{\pi }{4}\right)\)
\(\dfrac{\pi }{3}\) \(2\left( -\dfrac{1}{2}\right) =-1\) \(\left( -1,\dfrac{\pi }{3}\right)\)
\(\dfrac{\pi }{2}\) \(2\left( -1\right) =-2\) \(\left(-2,\dfrac{\pi }{2}\right)\)
\(\dfrac{2\pi }{3}\) \(2\left( -\dfrac{1}{2}\right) =-1\) \(\left( -1,\dfrac{2\pi }{3}\right)\)
\(\dfrac{3\pi }{4}\) \(2\left( 0\right) =0\) \(\left( 0,\dfrac{3\pi }{4}\right)\)
\(\dfrac{5\pi }{6}\) \(2\left( \dfrac{1}{2}\right) =1\) \(\left( 1,\dfrac{5\pi }{6}\right)\)
\(\pi\) \(2(1) =2\) \(( 2, \ \pi)\)
\(\dfrac{7\pi }{6}\) \(2\left( \dfrac{1}{2}\right) =1\) \(\left( 1,\dfrac{7\pi }{6}\right)\)
\(\dfrac{5\pi }{4}\) \(2(0) =0\) \(\left( 0,\dfrac{5\pi }{4}\right)\)
\(\dfrac{4\pi }{3}\) \(2\left( -\dfrac{1}{2}\right) =-1\) \(\left( -1,\dfrac{4\pi }{3}\right)\)
\(\dfrac{3\pi }{2}\) \(2\left( -1\right) =-2\) \(\left( -2,\dfrac{3\pi }{2}\right)\)
\(\dfrac{5\pi }{3}\) \(2\left( -\dfrac{1}{2}\right) =-1\) \(\left( -1,\dfrac{5\pi }{3}\right)\)
\(\dfrac{7\pi }{4}\) \(2\left(0\right) =0\) \(\left( 0,\dfrac{7\pi }{4}\right)\)
\(\dfrac{11\pi }{6}\) \(2\left( \dfrac{1}{2}\right) =1\) \(\left( 1,\dfrac{11\pi }{6}\right)\)
\( 2\pi\) \(2(1) =2\) \(( 2, \ 2\pi )\)
Figure 46 A rose with four petals.

(b) Parametric equations for \(r=2 \ \cos ( 2\theta )\): \begin{equation*} x=r \ \cos \theta =2 \ \cos ( 2\theta ) \ \cos \theta \qquad y=r \ \sin \theta =2 \ \cos ( 2\theta ) \ \sin \theta \end{equation*}

where \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.