Find the area of the region enclosed by the cardioid $r=1-\sin \theta ,\; 0\leq \theta \leq \dfrac{\pi }{2}.$

Solution The cardioid represented by $r=1-\sin \theta$ is shown in Figure 51(a) and the area enclosed by the cardioid from $\theta = 0$ to $\theta = \dfrac{\pi}{2}$ is shaded.

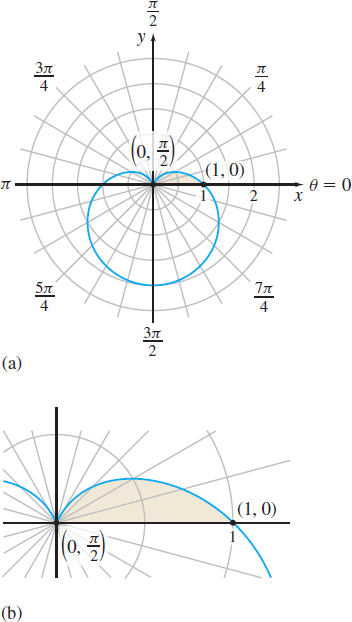
Figure 51 $r=1-\sin \theta ,\;0\leq \theta \leq \dfrac{\pi }{2}$

The region is swept out beginning with the ray $\theta =0$ and ending with the ray $\theta =\dfrac{\pi }{2}$, as shown in Figure 51(b). The limits of integration are $0$ and $\dfrac{\pi }{2}$ and the area $A$ is $$\begin{eqnarray*} A&=&\int_{\alpha }^{\beta }\frac{1}{2}r^{2}\,d\theta =\int_{0}^{\pi /2}\frac{1 }{2}(1-\sin \theta )^{2}\,d\theta =\frac{1}{2}\int_{0}^{\pi /2}(1-2\sin \theta +\sin ^{2}\theta )~d\theta \\[6pt] &=&\dfrac{1}{2}\int_{0}^{\pi /2}\left\{ 1-2\sin \theta +\frac{1}{2}[ 1-\cos ( 2\theta ) ] \right\} d\theta \qquad {\color{#0066A7}{\sin ^{2}\theta =\dfrac{1-\cos ( 2\theta )}{2}}} \\\\[5pt] &=&\frac{1}{2}\int_{0}^{\pi /2}\left[ \frac{3}{2}-2\sin \theta -\frac{1}{2}\cos ( 2\theta ) \right] d\theta\\[5pt] &=&\dfrac{1}{2}\left[ \dfrac{3}{2}\,\theta +2\cos \theta -\dfrac{1}{4}\sin ( 2\theta ) \right] _{0}^{\pi /2}=\dfrac{ 3\pi -8}{8} \end{eqnarray*}$$