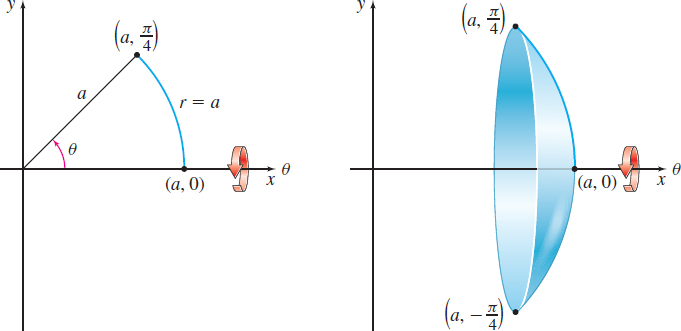
Find the surface area of the solid of revolution generated by revolving the arc of the circle $r=a,$ $a>0,$ $0\leq \theta \leq \dfrac{\pi }{4}$, about the polar axis.

Solution See Figure 55. We find the surface area $S$ using formula (1). Since $r=f(\theta )=a,\;f' ( \theta) =0.$ Then $$\begin{eqnarray*} S& =&2\pi \int_{\alpha }^{\beta }f(\theta )\sin \theta \sqrt{[ f(\theta )] ^{2}+[ f' ( \theta) ] ^{2}}~d\theta\\[4pt] &=&2\pi \int_{0}^{\pi /4}a\sin \theta \sqrt{a^{2}}\,d\theta =2\pi a^{2}\int_{0}^{\pi /4}\sin \theta \,d\theta \notag \\[4pt] & =&2\pi a^{2}\big[ -\cos \theta \big] _{0}^{\pi /4}=2\pi a^{2}\left( -\frac{\sqrt{2}}{2}+1\right) =\pi a^{2}( 2-\sqrt{2}) \end{eqnarray*}$$

Figure 55