Identifying and Graphing the Polar Equation of a Conic

(a) Identify and graph the equation \(r=\dfrac{4}{2-\cos \theta }\).

(b) Convert the polar equation to a rectangular equation.

(c) Find parametric equations for the polar equation.

Solution (a) We divide the numerator and the denominator by \(2\) to express the equation in the form \(r=\dfrac{ep}{1-e\cos \theta }.\) \[ r=\dfrac{4}{2-\cos \theta }=\dfrac{2}{1-\dfrac{1}{2}\cos \theta }\quad\quad {\color{#0066A7}{\hbox{\(r=\dfrac{ep}{1-e\cos \theta}\)}}} \]

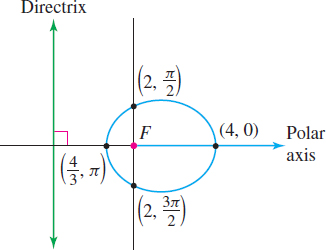
Now we see that \(e=\dfrac{1}{2}.\) Since \(ep=2,\) we find \(p=\dfrac{2}{e}=\dfrac{2}{\dfrac{1}{2}}=4.\) This is an ellipse, because \(e=\dfrac{1}{2}<1.\) One focus is at the pole, and the directrix is perpendicular to the polar axis a distance of \(p=4\) units to the left of the pole. The major axis is along the polar axis.

Letting \(\theta =0\) and \(\theta =\pi ,\) we can find the vertices of the ellipse. \[ \begin{equation*} r=\dfrac{4}{2-\cos 0}=\dfrac{4}{2-1}=4\qquad\hbox{and}\qquad r=\dfrac{4}{2-\cos \pi }=\dfrac{4}{2-\left( -1\right) }=\dfrac{4}{3} \end{equation*} \]

687

So, the vertices of the ellipse are the points whose polar coordinates are \(\left( 4,0\right)\) and \(\left( \dfrac{4}{3},\pi \right).\) The y-intercepts of the ellipse are at \(\theta=\dfrac{\pi}{2}\) and \(\theta= \dfrac{3\pi}{2}\), which give rise to the points \(\left(2,\dfrac{\pi}{2}\right)\) and \(\left(2,\dfrac{3\pi}{2}\right)\). The graph of the ellipse is shown in Figure 60.

(b) To obtain a rectangular equation of the ellipse, we eliminate the fraction and then square the resulting polar equation. \[ \begin{array}{rcl@{\qquad}l} r &=& \dfrac{4}{2-\cos \theta}\\ r\left( 2-\cos \theta \right) &=&4\\ 2r-r\cos \theta &=&4\\ 2r &=&4+r\cos \theta\\ 4r^{2} &=&\left( 4+r\cos \theta \right) ^{2} & {\color{#0066A7}{{\hbox{Square the equation.}}}} \\ 4( x^{2}+y^{2}) &=&( 4+x) ^{2} & {\color{#0066A7}{{\hbox{\(r^{2}=x^{2}+y^{2},\; x=r\cos \theta\)}}}} \\ 4x^{2}+4y^{2} &=&16+8x+x^{2} \\ 3\left( x^{2}-\dfrac{8}{3}x\right)+4y^{2} &=&16 \\ 3\left( x-\dfrac{4}{3}\right) ^{2}+4y^{2} &=&16+3\left( \dfrac{16}{9}\right) =\dfrac{64}{3} & {\color{#0066A7}{{\hbox{Complete the square in \(x\).}}}} \end{array} \]

This is the equation of an ellipse in rectangular coordinates, with its center at the point \(\left( \dfrac{4}{3},0\right)\) in rectangular coordinates.

(c) Parametric equations of the ellipse \(r=\dfrac{4}{2-\cos\theta }\) are \[ \begin{equation*} x( \theta) =r\cos \theta =\dfrac{4 \cos \theta }{2-\cos \theta }\qquad y( \theta) =r\sin \theta =\dfrac{4 \sin \theta }{2-\cos \theta }\;0\leq \theta \leq 2\pi \end{equation*} \] where \(\theta\) is the parameter.