Analyzing the Orbit of an Exoplanet

Many hundreds of planets beyond our solar system have been discovered. They are known as exoplanets. One of these exoplanets, HD 190360b, orbits the star HD 190360 (most stars do not have names) in an elliptical orbit given by the polar equation \[ r=\dfrac{3.575}{1-0.316 \cos \theta } \] where the star HD 190360 is at the pole, the major axis is along the polar axis, and \(r\) is measured in astronomical units (AU). (One AU \(=1.5\times 10^{11} {m},\) which is the average distance from Earth to the Sun.)

(a) What is the eccentricity of the exoplanet HD 190360b’s orbit?

(b) Find the distance from the exoplanet HD 190360b to the star HD 190360 at periapsis (shortest distance).

(c) Find the distance from the exoplanet HD 190360b to the star HD 190360 at apoapsis (greatest distance).

Solution (a) The equation of HD 190360b’s orbit is in the form \(r=\dfrac{ep}{1-e\cos \theta }.\) So, the eccentricity of the orbit is \(e=0.316.\) See Figure 61.

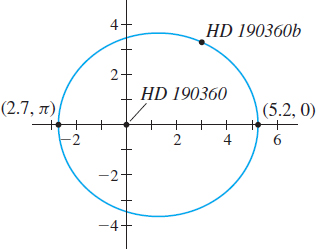
(b) Periapsis occurs when \(r\) is a minimum. Since \(r\) is minimum when \(\cos \theta =-1,\) periapsis occurs for \[ \begin{equation*} r=\dfrac{3.575}{1-0.316 \cos \theta }=\dfrac{3.575}{1-0.316( -1) }= \dfrac{3.575}{1.316}\approx 2.717 \end{equation*} \]

The periapsis is at the point \(( 2.717,\pi ) .\) The exoplanet HD 190360b is approximately \(2.717\) AU from the star HD 190360 at periapsis.

(c) The apoapsis occurs when \(r\) is a maximum. Since \(r\) is maximum when \(\cos \theta =1,\) the apoapsis occurs for \[ r=\dfrac{3.575}{ 1-0.316 \cos \theta}=\dfrac{3.575}{1-0.316(1) }=\dfrac{3.575}{0.684} \approx 5.227 \]

The apoapsis is at the point \(( 5.227,0)\). The exoplanet HD 190360b is approximately \(5.227\) AU from the star HD 190360 at apoapsis.