Graph the plane curve represented by the parametric equations $$\begin{equation*} x( t) =3t^{2} \qquad y( t) =2t\;-2\leq t\leq 2 \end{equation*}$$

Indicate the orientation of the curve.

Solution Corresponding to each number $t$, $-2\leq t\leq 2,$ there are a number $x$ and a number $y$ that are the coordinates of a point $( x,y)$ on the curve. We form a table listing various choices of the parameter $t$ and the corresponding values for $x$ and $y$, as shown in Table 1.

The motion begins when $t=-2$ at the point $( 12,-4)$ and ends when $t=2$ at the point $( 12,4)$. Figure 2 illustrates the plane curve whose parametric equations are $x( t) =3t^{2}$ and $y( t) =2t$. The arrows indicate the orientation of the plane curve for increasing values of the parameter $t$.

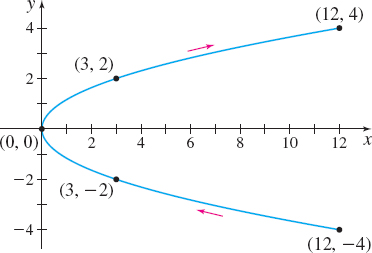
Figure 2 $x(t)=3t^{2}, y(t)=2t, -2\le t \le 2$