Finding a Rectangular Equation for a Plane Curve Represented Parametrically

Find rectangular equations for the plane curves represented by each of the parametric equations. Graph each curve and indicate its orientation.

(a) \(x( t) =R\, \cos t\quad y( t) = R\, \sin t\quad 0\leq t\leq \pi \) and \(R> 0\)

(b) \(x( t) =R\, \sin t\quad y( t) = R\, \cos t\quad 0\leq t\leq \pi \) and \(R> 0\)

Solution (a) We eliminate the parameter \(t\) using a Pythagorean Identity. \[ \begin{eqnarray*} \cos^{2}t+\sin ^{2}t &=&1 \\ \left( \dfrac{x}{R}\right) ^{2}+\left( \dfrac{y}{R}\right) ^{2} &=&1 \qquad \color{#0066A7}{\cos t=\dfrac{x}{R},\quad \sin t=\dfrac{y}{R}} \\ x^{2}+y^{2} &=&R^{2} \tag{1} \end{eqnarray*} \]

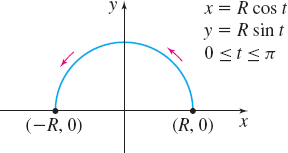
The rectangular equation represents a circle with radius \(R\) and center at the origin. In the parametric equations, \(0\leq t\leq \pi\), so the curve begins when \(t=0\) at the point \(( R, 0) \), passes through the point \(( 0, R) \) when \(t=\dfrac{\pi }{2}\), and ends when \(t=\pi \) at the point \(( -R,0)\). The curve is an upper semicircle of radius \(R\) with counterclockwise orientation, as shown in Figure 4. If we solve equation (1) for \(y\), we obtain the rectangular equation of the semicircle \[ y=\sqrt{R^{2}-x^{2}}\qquad\hbox{where }-R\leq x\leq R \]

(b) We eliminate the parameter \(t\) as we did in (a), and again we obtain \[ \begin{eqnarray*} x^{2}+y^{2}=R^{2}\tag{2} \end{eqnarray*} \]

The rectangular equation represents a circle with radius \(R\) and center at \(( 0,0) \). But in the parametric equations, \(0\leq t\leq \pi \), so now the curve begins when \(t=0\) at the point \(( 0, R)\), passes through the point \(( R, 0) \) when \(t=\dfrac{\pi }{2}\), and ends at the point \(\left( 0,-R\right) \) when \(t=\pi\). The curve is a right semicircle of radius \(R\) with a clockwise orientation, as shown in Figure 5. If we solve equation (2) for \(x\), we obtain the rectangular equation of the semicircle \[ x=\sqrt{R^{2}-y^{2}}\qquad \hbox{where }-R\leq y\leq R \]