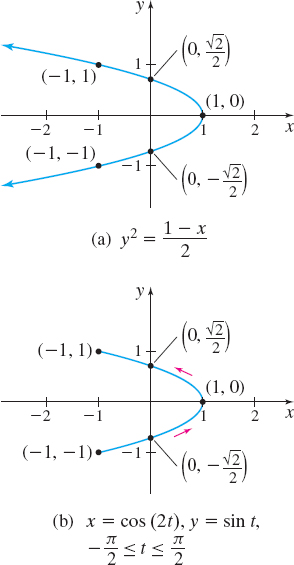
Finding a Rectangular Equation for a Plane Curve Represented Parametrically

(a) Find a rectangular equation of the plane curve whose parametric equations are \[ x( t) =\cos ( 2t) \qquad y( t) =\sin t\quad -\dfrac{\pi }{2}\leq t\leq \dfrac{\pi }{2} \]

(b) Graph the rectangular equation.

(c) Determine the restrictions on \(x\) and \(y\) so the graph corresponding to the rectangular equation is identical to the plane curve described by \[ x=x( t)\qquad y=y( t)\quad -\dfrac{\pi }{2} \leq t\leq\dfrac{\pi}{2} \]

(d) Graph the plane curve whose parametric equations are \[ x=\cos ( 2t)\qquad y=\sin t\quad -\dfrac{\pi }{2}\leq t\leq \dfrac{\pi }{2} \]

Solution (a) To eliminate the parameter \(t\), we use a trigonometric identity that involves \(\sin t\) and \(\cos ( 2t)\), namely, \(\sin ^{2}t=\dfrac{1-\cos ( 2t) }{2}\). Then \[ \begin{equation*} y^{2}\underset{\color{#0066A7}{\underset{\hbox{\(y( t) =\sin t\)}}{{\uparrow }}}}{=}\sin ^{2}t=\dfrac{1-\cos (2t) }{2}\underset{\color{#0066A7}{\underset{\hbox{\(x( t)=\cos ( 2t)\)}}{{\uparrow }}}}{=}\dfrac{1-x}{2}\\ \end{equation*} \]

(b) The curve represented by the rectangular equation \(y^{2}=\dfrac{1-x}{2} \) is the parabola shown in Figure 6(a).

(c) The plane curve represented by the parametric equations does not include all the points on the parabola. Since \(x( t) =\cos ( 2t) \) and \(-1\leq \cos ( 2t) \leq 1\), then \(-1\leq x\leq 1\). Also, since \(y( t) =\sin t\), then \(-1\leq y\leq 1\). Finally, the curve is traced out exactly once in the counterclockwise direction from the point \(( -1,-1) \) (when \(t=-\dfrac{\pi }{2}\)) to the point \(( -1,1) \) (when \(t=\dfrac{\pi }{2}\)).

(d) The plane curve represented by the given parametric equations is the part of the parabola shown in Figure 6(b).