EXAMPLE 5Using Time as the Parameter in Parametric Equations
Describe the motion of an object that moves along a curve so that at time t it has coordinates x(t)=3costy(t)=4sint0≤t≤2π
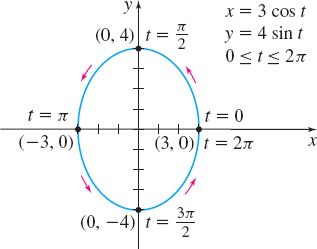
Figure 7 x29+y216=1.
Solution We eliminate the parameter t using the Pythagorean Identity cos2t+sin2t=1. x29+y216=1cost=x3,sint=y4
The plane curve is the ellipse shown in Figure 7. When t=0, the object is at the point (3,0). As t increases, the object moves around the ellipse in a counterclockwise direction, reaching the point (0,4) when t=π2, the point (−3,0) when t=π, the point (0,−4) when t=3π2, and returning to its starting point (3,0) when t=2π.
641