(a) Find an equation of the tangent line to the plane curve with parametric equations $x(t) =3t^{2},\quad y(t) =2t$, when $t=1$.

(b) Find all the points on the plane curve at which the tangent line is vertical.

Solution (a) The curve is smooth $\bigg(\dfrac{{\it dy}}{{\it dt}}=2 {\rm \, is \, never \, zero} \bigg)$. Since $\dfrac{dx}{dt}=6t$ is not 0 at $t=1$, the slope of the tangent line to the curve is $$\begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{\dfrac{d}{dt} ( 2t) }{\dfrac{d}{dt}\left( 3t^{2}\right) }=\dfrac{2}{6t}=\frac{1 }{3t} \end{equation*}$$

When $t=1$, the slope of the tangent line is $\dfrac{1}{3}$. Since $x=3$ and $y=2$ when $t=1$, an equation of the tangent line is $$\begin{array}{rcl@{\qquad\qquad}l} y-2 &=&\dfrac{1}{3} ( x-3 ) & {\color{#0066A7}{{y-y_{1} =m( x-x_{1});}}\;{\color{#0066A7}{ x_{1} =3, y_{1} =2, m= \dfrac{1}{3}}}} \\ y &=&\dfrac{1}{3}x+1 \end{array}$$

649

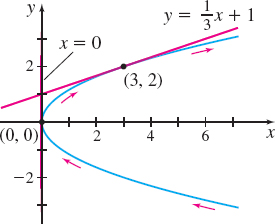
Figure 13 $x(t)=3t^2,\quad y(t) = 2t$

(b) A vertical tangent line occurs when $\dfrac{dx}{dt}=0$ and $\dfrac{dy}{dt}\neq 0.$ Since $\dfrac{dx}{dt}=0$ and $\dfrac{dy}{ dt}=2$ when $t=0,$ there is a vertical tangent line to the curve when $t=0,$ namely at the point $(0,0)$.