Consider the cycloid defined by $$\begin{equation*} x(t) =a(t-\sin t)\qquad y(t) =a(1-\cos t)\qquad 0<t<2\pi \qquad a>0 \end{equation*}$$

(a) Show that the slope of the tangent line to the cycloid is given by $\dfrac{\sin t}{1-\cos t}$.

(b) Find any points where the tangent line to the cycloid is horizontal.

Solution (a) $$\begin{align*} x(t)&=at-a\sin t& y(t)=a-a\cos t \\ \dfrac{dx}{dt}&=a-a\cos t&\dfrac{dy}{dt}=a\sin t \end{align*}$$

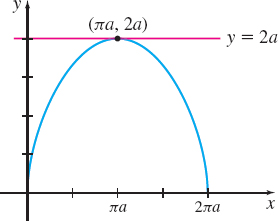
Figure 14 $x(t)=a(t-\sin t),\\ y(t)=a(1-\cos t),\\ 0< t < 2\pi$

For $0<t<2\pi, {\dfrac{dx}{dt}} = a(1-\cos t) \neq 0$. Then the slope of the tangent line is $$\begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{a\sin t}{a(1-cost)}=\frac{\sin t}{1-\cos t} \end{equation*}$$

(b) The cycloid has a horizontal tangent line when $\dfrac{dy}{dt} =a\sin t=0,$ but $\dfrac{dx}{dt}\neq 0.$ For $0<t<2\pi$, we have $a\sin t=0$ when $t=\pi$. Since $\dfrac{dx}{dt}\neq 0$ for $0< t< 2\pi ,$ the cycloid has a horizontal tangent line when $t=\pi ,$ at the point $(\pi a,2a)$. The equation of the horizontal tangent line is $y=2a$, as shown in Figure 14.