Finding an Equation of the Tangent Line to a Smooth Curve

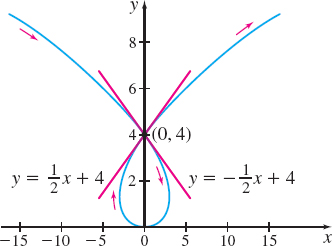
The plane curve represented by the parametric equations \(x(t)=t^{3}-4t,\quad y(t) =t^{2}\), crosses itself at the point \((0,4)\), and so has two tangent lines there, as shown in Figure 15. Find equations for these tangent lines.

Solution We begin by finding the numbers \(t\) that correspond to the point \(( 0,4) .\) \[ \begin{array}{rcl@{\quad\qquad}lrll} x &=&0 & y&=&4 \\ t^{3}-4t &=&0 & t^{2}&=&4 \\ t( t^{2}-4) &=& 0 & t&=&-2\hbox{ or }2 \\ t &=&0,-2,\hbox{or }2 & \end{array} \]

We exclude \(t=0,\) since if \(t=0,\) then \(y\neq 4.\) So we investigate only \( t=-2\) and \(t=2.\) Since \(\dfrac{dx}{dt}=3t^{2}-4\neq 0\) for \(t=-2\) and \(t=2,\) the slope of the tangent lines is given by \[ \begin{equation*} \frac{dy}{dx}=\frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\frac{\dfrac{d}{dt} ( t^{2}) }{\dfrac{d}{dt}( t^{3}-4t) }=\dfrac{2t}{ 3t^{2}-4} \end{equation*} \]

650

When \(t=-2\), the slope of the tangent line is \[ \begin{equation*} \dfrac{dy}{dx}=\dfrac{2( -2) }{3( -2) ^{2}-4}=\dfrac{-4 }{8}=-\dfrac{1}{2} \end{equation*} \]

and an equation of the tangent line at the point \(( 0,4) \) is \[ \begin{eqnarray*} y-4 &=&-\dfrac{1}{2}( x-0) \\ y &=&-\dfrac{1}{2}x+4 \end{eqnarray*} \]

When \(t=2\), the slope of the tangent line at the point \(( 0,4) \) is \[ \begin{equation*} \dfrac{dy}{dx}=\dfrac{2( 2) }{3( 2) ^{2}-4}=\dfrac{4}{8 }=\dfrac{1}{2} \end{equation*} \]

and an equation of the tangent line at \(( 0,4) \) is \[ \begin{eqnarray*} y-4 &=&\dfrac{1}{2}( x-0) \\ y &=&\dfrac{1}{2}x+4 \end{eqnarray*} \]