Finding Arc Length for Parametric Equations

Find the length \(s\) of the curve represented by the parametric equations \[ \begin{equation*} x(t) =t^{3}+2\qquad\hbox{}\qquad y(t) =2t^{9/2} \end{equation*} \]

from the point where \(t=1\) to the point where \(t=3\). Figure 16 shows the graph of the curve.

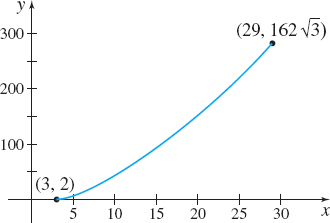
Solution We begin by finding the derivatives \(\dfrac{dx}{dt}\) and \(\dfrac{dy}{dt}.\) \[ \begin{equation*} \dfrac{dx}{dt}=3t^{2}\qquad\hbox{and}\qquad \dfrac{dy}{dt}=9t^{7/2} \end{equation*} \]

The curve is smooth for \(1\leq t\leq 3.\) Now using the arc length formula for parametric equations, we have \[ \begin{eqnarray*} s&=&\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}}~dt=\int_{1}^{3}\sqrt{(3t^{2})^{2}+(9t^{7/2})^{2}} \,dt\\[6pt] &=&\int_{1}^{3}\sqrt{9t^{4}+81\,t^{7}}\,dt =\int_{1}^{3}3t^{2}\sqrt{1+9t^{3} }\,dt \end{eqnarray*} \]

We use the substitution \(u=1+9t^{3}\). Then \(du=27t^{2}dt,\) or equivalently, \(3t^{2}dt=\dfrac{du}{9}.\) Changing the limits of integration, we find that when \(t=1,\) then \(u=10;\) and when \(t=3,\) then \(u=1+9\cdot 3^{3}=244.\) The arc length \(s\) is \[ \begin{eqnarray*} s&=&\int_{1}^{3}3t^{2}\sqrt{1+9t^{3}}\,dt=\int_{10}^{244}\sqrt{u}\left( \frac{ du}{9}\right) =\dfrac{1}{9}\int_{10}^{244}u^{1/2}du=\frac{1}{9}\left[ \frac{ u^{3/2}}{\dfrac{3}{2}}\right] _{10}^{244}\\ &=&\frac{2}{27}[244^{3/2}-10^{3/2}] = \frac{4}{27}\big[244\sqrt{61}- 5\sqrt{10}\big] \end{eqnarray*} \]