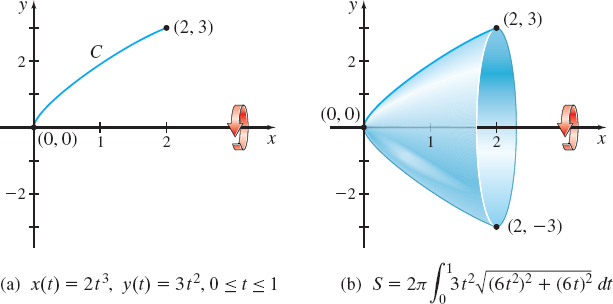
Finding the Surface Area of a Solid of Revolution Obtained from Parametric Equations
Find the surface area of the solid generated by revolving the smooth curve \( C \) represented by the parametric equations \(x(t) =2t^{3},\) \(y(t) =3t^{2},\) \(0\leq t\leq 1\), about the \(x\)-axis.
We use formula (2) with \(\dfrac{dx}{dt}=\dfrac{d}{dt}\,\left( 2t^{3}\right) =6t^{2}\) and \( \dfrac{dy}{dt}=\dfrac{d}{dt}\,\left( 3t^{2}\right) =6t\). Then \begin{eqnarray*} S &=&2\pi \int_{a}^{b}\,y(t) \, \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{ dy}{dt}\right) ^{2}}\,dt=2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{( 6t^{2})^{2}+( 6t) ^{2}}\,dt\\[5pt] &=&2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{36t^{4}+36t^{2}}\,dt =36\pi \int_{0}^{1}\,t^{3}\,\sqrt{t^{2}+1}\,dt=\frac{36\pi }{2}\int_{1}^{2}\,(u-1)\sqrt{u}\,du\\[-10pt] &&\hspace{10.9pc}\underset{\underset{{{\color{#00ADEE}{{\hbox{when \(t=0, u=1;\) when \(t=1, u=2\)}}}}}}{\color{#00ADEE}{{{\hbox{\(u=t^{2}+1;\)}}} {\color{#00ADEE}{\hbox{\(du=2t dt\)}}}} \,} }{\color{#00ADEE}{{{\uparrow }}}}\\[-3pt] &=&18\pi\,\left[ \dfrac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}\right]_{1}^{2}=\frac{24\pi }{5}\,(\sqrt{2}+1) \end{eqnarray*}
The surface area of the solid of revolution is \(\dfrac{24\pi }{5}(\sqrt{2} +1)\approx 36.405\) square units.