Finding the Surface Area of a Solid of Revolution Obtained from a Rectangular Equation

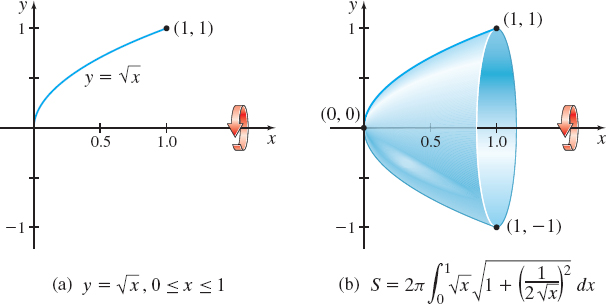
Find the surface area of the solid generated by revolving the curve represented by \(y= \sqrt{x},\) from \(x=0\) to \(x=1\), about the \(x\)-axis.

Solution We begin with the graph of \(y=\sqrt{x} ,\) \(0\leq x\leq 1,\) and revolve it about the \(x\)-axis, as shown in Figure 23.

We use formula (3) with \(f( x) = \sqrt{x}\) and \(f’ ( x) =\dfrac{1}{2 \sqrt{x}}.\) The surface area \(S\) we seek is

The surface area of the solid of revolution is \(\dfrac{\pi }{6}(5 \sqrt{5} -1)\approx 5.330\) square units.