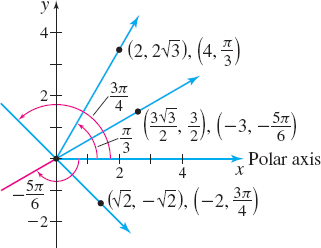
Converting from Polar Coordinates to Rectangular Coordinates

Find the rectangular coordinates of each point whose polar coordinates are:

(a) \(\left( 4,\dfrac{\pi }{3}\right)\)

(b) \(\left( -2,\dfrac{3\pi }{4}\right)\)

(c) \(\left(-3,-\dfrac{5\pi }{6}\right)\)

Solution (a) We use the equations \(x=r\cos \theta\) and \(y=r\sin \theta\) with \(r=4\) and \(\theta =\dfrac{\pi }{3}.\) \[ x=4\cos \dfrac{\pi }{3}=4\left( \dfrac{1}{2}\right) =2 \qquad \hbox{and} \qquad y=4\sin \dfrac{\pi }{3}=4\left( \dfrac{\sqrt{3}}{2}\right) =2\sqrt{3} \]

The rectangular coordinates are \((2,2\sqrt{3}).\)

(b) We use the equations \(x=r\cos \theta\) and \(y=r\sin \theta\) with \(r=-2\) and \(\theta =\dfrac{3\pi }{4}.\) \[ x=-2\cos \dfrac{3\pi }{4}=-2\left(-\dfrac{\sqrt{2}}{2}\right) =\sqrt{2} \quad\hbox{and}\quad y=-2\sin \dfrac{3\pi }{4}=-2\left( \dfrac{\sqrt{2}}{2}\right) =-\sqrt{2} \]

The rectangular coordinates are \(( \sqrt{2},-\sqrt{2}) .\)

(c) We use the equations \(x=r\cos \theta\) and \(y=r\sin \theta\) with \(r=-3\) and \(\theta =-\dfrac{5\pi }{6}.\) \[ \begin{eqnarray*} x&=&-3\cos \left( -\dfrac{5\pi }{6}\right) =-3\left( -\dfrac{\sqrt{3}}{2} \right) =\dfrac{3\sqrt{3}}{2}\;\hbox{}\; \\[4pt] y&=&-3\sin \left( -\dfrac{5\pi }{6}\right) =-3\left( -\dfrac{1}{2}\right) =\dfrac{3}{2} \end{eqnarray*} \]

The rectangular coordinates are \(\left( \dfrac{3\sqrt{3}}{2},\dfrac{3}{2}\right)\).