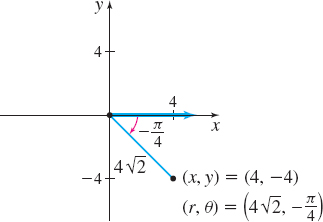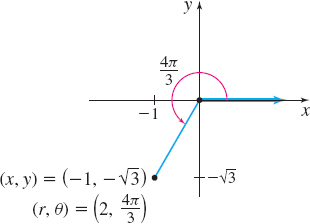Converting from Rectangular Coordinates to Polar Coordinates

Find polar coordinates of each point whose rectangular coordinates are:

(a) \((4,-4)\)

(b) \(( -1,-\sqrt{3})\)

(c) \(( 4,-1)\)

Solution (a) The point \(( 4,-4)\), plotted in Figure 35, is in quadrant IV. The distance from the pole to the point \((4,-4)\) is \[ \begin{equation*} r=\sqrt{x^{2}+y^{2}}=\sqrt{4^{2}+( -4) ^{2}}=\sqrt{32}=4\sqrt{2} \end{equation*} \]

Since the point \(( 4,-4)\) is in quadrant IV, \(-\dfrac{\pi }{2} <\theta <0.\) So, \[ \begin{equation*} \theta =\tan ^{-1}\left( \dfrac{y}{x}\right) =\tan ^{-1}\left( \dfrac{-4}{4}\right) =\tan ^{-1}( -1) =-\dfrac{\pi }{4} \end{equation*} \]

666

A pair of polar coordinates for this point is \(\left( 4\sqrt{2},-\dfrac{\pi }{4}\right) .\) Other possible representations include \(\left( -4\sqrt{2}, \dfrac{3\pi }{4}\right)\) and \(\left( 4\sqrt{2},\dfrac{7\pi }{4}\right)\).

(b) The point \(( -1,-\sqrt{3}) ,\) plotted in Figure 36, is in quadrant III. The distance from the pole to the point \(( -1,-\sqrt{3})\) is \[ \begin{equation*} r=\sqrt{( -1) ^{2}+( -\sqrt{3}) ^{2}}=\sqrt{1+3}=2 \end{equation*} \]

Since the point \(( -1,-\sqrt{3})\) lies in quadrant III and the inverse tangent function gives an angle in quadrant I, we add \(\pi\) to \(\tan ^{-1}\left( \dfrac{y}{x}\right)\) to obtain an angle in quadrant III. \[ \begin{equation*} \theta =\tan ^{-1}\left( \dfrac{-\sqrt{3}}{-1}\right) +\pi =\tan ^{-1}( \sqrt{3}) +\pi =\dfrac{\pi }{3}+\pi =\dfrac{4\pi }{3} \end{equation*} \]

A pair of polar coordinates for the point is \(\left( 2,\dfrac{4\pi }{3} \right)\). Other possible representations include \(\left( -2,\dfrac{\pi }{3} \right)\) and \(\left( 2,-\dfrac{2\pi }{3}\right)\).

(c) The point \(\left( 4,-1\right) ,\) plotted in Figure 37, lies in quadrant IV. The distance from the pole to the point \(( 4,-1)\) is \[ \begin{equation*} r=\sqrt{x^{2}+y^{2}}=\sqrt{4^{2}+( -1) ^{2}}=\sqrt{17} \end{equation*} \]

Since the point \(( 4,-1)\) is in quadrant IV, \(-\dfrac{\pi }{2}<\theta <0.\) So, \[ \begin{equation*} \theta =\tan ^{-1}\left( \dfrac{y}{x}\right) =\tan ^{-1}\left( \dfrac{-1}{4} \right) \approx -0.245\hbox{ radians} \end{equation*} \]

A pair of polar coordinates for this point is \(( \sqrt{17} ,-0.245) .\) Other possible representations for the point include \(\left( \sqrt{17} ,\tan ^{-1}\left( -\dfrac{1}{4}\right) +2\pi \right) \approx ( \sqrt{17} ,6.038)\) and \(\left( -\sqrt{17},\tan ^{-1}\left( -\dfrac{1}{4}\right) +\pi \right) \approx ( -\sqrt{17},2.897)\).