Identify and graph each equation:

(a) $r=3$

(b) $\theta =\dfrac{\pi }{4}$

Figure 39 $r=3$ or $x^{2} + y^{2} = 9$.

Solution (a) If $r$ is fixed at $3$ and $\theta$ is allowed to vary, the graph is a circle with its center at the pole and radius 3, as shown in Figure 39. To confirm this, we convert the polar equation $r=3$ to a rectangular equation. $$\begin{array}{rcl@{\qquad}l} r &=&3 \\ r^{2} &=&9\quad{\color{#0066A7}{{\hbox{Square both sides.}}}} \\ x^{2}+y^{2} &=&9\quad{\color{#0066A7}{{\hbox{\(r^{2} =x^{2} +y^{2}\)}}}} \end{array}$$

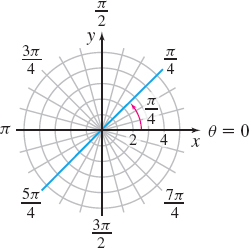
Figure 40 $\theta =\dfrac{\pi }{4}$ or $y=x$.

(b) If $\theta$ is fixed at $\dfrac{\pi }{4}$ and $r$ is allowed to vary, the result is a line containing the pole, making an angle of $\dfrac{\pi }{4}$ with the polar axis. That is, the graph of $\theta =\dfrac{\pi }{4}$ is a line containing the pole with slope $\tan \theta =\tan \dfrac{\pi }{4}=1$, as shown in Figure 40. To confirm this, we convert the polar equation to a rectangular equation. $$\begin{array}{rcl} \theta &=&\dfrac{\pi }{4} \\ \tan \theta &=&\tan \dfrac{\pi }{4} \\ \dfrac{y}{x} &=&1 \\ y &=&x \end{array}$$