Identifying and Graphing Polar Equations

Identify and graph the equations:

(a) \(r\sin \theta =2\)

(b) \(r=4\sin \theta\)

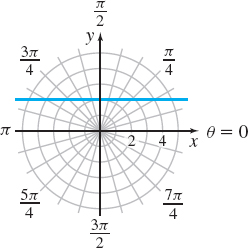
Solution (a) Here, both \(r\) and \(\theta\) are allowed to vary, so the graph of the equation is not as obvious. If we use the fact that \(y=r\sin \theta ,\) the equation \(r\sin \theta =2\) becomes \(y=2.\) So, the graph of \(r\sin \theta =2\) is the horizontal line \(y=2\) that lies \(2\) units above the pole, as shown in Figure 41.

(b) To convert the equation \(r=4\sin \theta\) to rectangular coordinates, we multiply the equation by \(r\) to obtain \[ \begin{equation*} r^{2}=4r\sin \theta \end{equation*} \]

Now we use the formulas \(r^{2}=x^{2}+y^{2}\) and \(y=r\sin \theta\). Then \[ \begin{array}{rcl@{\qquad}l} r^{2} &=&4r\sin \theta \\ x^{2}+y^{2} &=&4y & {\color{#0066A7}{{\hbox{\(r^{2} =x^{2} + y^{2},\;r\sin \theta =y\)}}}} \\ x^{2}+(y^{2}-4y) &=&0 \\ x^{2}+\left( y^{2}-4y+4\right) &=&4 & {\color{#0066A7}{{\hbox{Complete the square in \(y\).}}}} \\ x^{2}+(y-2)^{2} &=&4 & {\color{#0066A7}{{\hbox{Factor.}}}} \end{array} \]

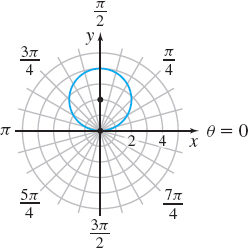
This is the standard form of the equation of a circle with its center at the point \(( 0,2)\) and radius \(2\) in rectangular coordinates. See Figure 42. Notice that the circle passes through the pole.