1. True or False If $\mathbf{v}$ is a nonzero vector, then $\mathbf{v\,{\cdot}\, v}=\left\Vert \mathbf{v}\right\Vert$.

2. True or False If two nonzero vectors $\mathbf{v}$ and $\mathbf{w}$ are parallel, then $\mathbf{v\,{\cdot}\, w}=0$.

3. If $\theta$ is the angle between two nonzero vectors $\mathbf{v}$ and $\mathbf{w}$, then $\cos \theta$ = _______.

4. True or False If $\mathbf{v}=v_{1}\mathbf{i}+v_{2} \mathbf{j}+v_{3}\mathbf{k}$ is a nonzero vector in space, then $\mathbf{v} =\left\Vert \mathbf{v}\right\Vert \left[ \cos \alpha \mathbf{i}+\cos \beta \mathbf{j}+\cos \gamma \mathbf{k}\right]$, where $\cos \alpha =\dfrac{v_{1} }{\Vert \mathbf{v}\Vert },$ $\cos \beta =\dfrac{v_{2}}{\Vert \mathbf{v}\Vert },$ and $\cos \gamma =\dfrac{v_{3}}{\Vert \mathbf{v}\Vert }.$

5. True or False The dot product of two vectors is sometimes called the vector product.

6. True or False For any two nonzero vectors $\mathbf{v}$ and $\mathbf{w}$, the vector $\mathbf{v}$can be decomposed into two vectors, one parallel to $\mathbf{w}$ and the other orthogonal to $\mathbf{w}$.

7. $\mathbf{v}=2\mathbf{i}-3\mathbf{j}+\mathbf{k},\quad \mathbf{w}=\mathbf{i}-\mathbf{j}+\mathbf{k}$

8. $\mathbf{v}=-3\mathbf{i}+2\mathbf{j}-\mathbf{k},\quad \mathbf{w}=2\mathbf{i}+\mathbf{j}-\mathbf{k}$

9. $\mathbf{v}=\mathbf{i}-\mathbf{j},\quad \mathbf{w}=\mathbf{j}+\mathbf{k}$

10. $\mathbf{v}=\mathbf{j}-\mathbf{k},\quad \mathbf{w}=\mathbf{i}+\mathbf{k}$

11. $\mathbf{v}=3\mathbf{i}+\mathbf{j}-\mathbf{k},\quad \mathbf{w}=-2\mathbf{i}-\mathbf{j}+\mathbf{k}$

12. $\mathbf{v}=\mathbf{i}-3\mathbf{j}+4\mathbf{k},\quad \mathbf{w}=4\mathbf{i}-\mathbf{j}+3\mathbf{k}$

13. $\mathbf{v}=\mathbf{i}-\mathbf{j},\quad \mathbf{w}=\mathbf{i}+\mathbf{j}$

14. $\mathbf{v}=3\mathbf{i\,+\,}4\mathbf{j},\quad \mathbf{w}=-6\mathbf{i}-8\mathbf{j}$

15. $\mathbf{v}=2a\mathbf{i}+\mathbf{j}-\mathbf{k},\quad \mathbf{w}=\mathbf{i}-\mathbf{j}+\mathbf{k}$

16. $\mathbf{v}=\mathbf{i}+2a\mathbf{j}-\mathbf{k},\quad \mathbf{w}=\mathbf{i}-\mathbf{j}+\mathbf{k}$

17. $\mathbf{v}=a\mathbf{i}+\mathbf{j}+\mathbf{k},\quad \mathbf{w}=\mathbf{i}+a\mathbf{j}+4\mathbf{k}$

18. $\mathbf{v}=\mathbf{i}-a\mathbf{j}+2\mathbf{k},\quad \mathbf{w}=2a\mathbf{i}+\mathbf{j}+\mathbf{k}$

19. $\mathbf{v}=3\mathbf{i}-6\mathbf{j}-2\mathbf{k}$

20. $\mathbf{v}=-6\mathbf{i}+12\mathbf{j}+4\mathbf{k}$

21. $\mathbf{v=i+j+k}$

22. $\mathbf{v=i-j-k}$

23. $\mathbf{v=i-k}$

24. $\mathbf{v=j+k}$

25. $\mathbf{v}=3\mathbf{i}-5\mathbf{j}+2\mathbf{k}$

26. $\mathbf{v}=2\mathbf{i}+3\mathbf{j}-4\mathbf{k}$

27. $\mathbf{v}=2\mathbf{i}-3\mathbf{j}+\mathbf{k},\quad \mathbf{w}=\mathbf{i}-\mathbf{j}+\mathbf{k}$

28. $\mathbf{v}=-3\mathbf{i}+2\mathbf{j}-\mathbf{k},\quad \mathbf{w}=2\mathbf{i}+\mathbf{j}-\mathbf{k}$

29. $\mathbf{v}=\mathbf{i}-\mathbf{j},\quad \mathbf{w}=\mathbf{j}+\mathbf{k}$

30. $\mathbf{v}=\mathbf{j}-\mathbf{k},\quad \mathbf{w}=\mathbf{i}+\mathbf{k}$

31. $\mathbf{v}=3\mathbf{i}+\mathbf{j}-\mathbf{k},\quad \mathbf{w}=-2\mathbf{i}-\mathbf{j}+\mathbf{k}$

32. $\mathbf{v}=\mathbf{i}-3\mathbf{j}+4\mathbf{k},\quad \mathbf{w}=4\mathbf{i}-\mathbf{j}+3\mathbf{k}$

33. Find a scalar $a$ so that the angle between the vectors $\mathbf{v}=a\mathbf{i}+\mathbf{j}+\mathbf{k}$ and $\mathbf{w}=\mathbf{i}+a \mathbf{j}+\mathbf{k}$ is $\dfrac{\pi }{3}$.

34. Find a scalar $a$ so that the angle between the vectors $\mathbf{v}=a\mathbf{i}-\mathbf{j}+\mathbf{k}$ and $\mathbf{w}=\mathbf{i}- \mathbf{j}+a\mathbf{k}$ is $\dfrac{2\pi }{3}$.

35. Ground Speed and Direction An airplane flying due north has an air speed of 500 km/h. There is a northwesterly wind of 60 km/h. Find the true speed and direction of the plane relative to the ground.

36. Ground Speed and Direction A bird flying west has an air speed of 12 km/h. If there is a southeasterly wind of 5 km/h, find the true speed and direction of the bird relative to the ground.

37. Steering a Boat A stream 1 km wide has a constant current of 5 km/h. At what angle to the shore should a person navigate a boat, which is maintaining a constant speed of 15 km/h, in order to reach a point directly opposite?

38. Swimming to a Destination A river is 500 m wide and has a current of 1 km/h. If a swimmer can swim at a constant speed of 2 km/h, at what angle to the shore should she swim if she wishes to reach the shore at a point directly opposite? How long will it take her to cross the river?

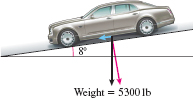
39. Braking Load A car with a gross weight of 5300 lb is parked on a street with an 8$^\circ$grade, as shown in the figure below. Find the magnitude of the force required to keep the car from rolling down the street. What is the magnitude of the force perpendicular to the street?

40. Ramp Angle Billy stops while rolling a 250-lb piano up a ramp. If the angle of inclination of the ramp is 20$^\circ$, how many pounds of force must Billy exert to hold the piano in position?

41. Work A wagon is pulled horizontally by exerting a force of $20$ lb on the handle at an angle of 30$^\circ$ with the horizontal. How much work is done in moving the wagon $100$ ft?

42. Work Find the work done by a force of 1 N acting in the direction $2\mathbf{i}+2\mathbf{j}+\mathbf{k}$ in moving an object 3 m from (0, 0, 0) to (1, 2, 2).

723

43. Work Find the work done by a force of 3 N acting in the direction $2\mathbf{i+j}+2\mathbf{k}$ in moving an object 2 m from (0, 0, 0) to (0, 2, 0).

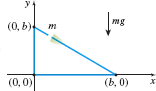
44. Work Find the work done by gravity when an object of mass $m$ moves once around the triangle shown in the figure. (The force of gravity is $mg$, where $g=9.80 {~\text m}/\text{s}^{2}$.)

    

45. Work Two workers, A and B, are each pulling identical crates of tools a distance of 10 m along a level floor. Worker A pulls the crate with a force of 850 N at an angle of 30$^\circ$with respect to the floor, and Worker B also pulls the crate with a force of 850 N, but at an angle of 45$^\circ$ with respect to the floor. Assume that in both cases, the crates are moved from (0, 0, 0) to (10, 0, 0), and the $z$-axis points upward, perpendicular to the floor.

    1. (a) Find the amount of work done by each person in moving the crate.
    2. (b) Which person do you think took less time moving the crate? Explain your reasoning.

46. A horse pulls a plow a distance of 15 meters along the ground from (0, 0) to (15, 0), during which a force of 725 newtons is applied at an angle of 15$^{\circ}$ with respect to the ground.

    1. (a) What is the work done by the horse?
    2. (b) During this motion, the force of friction is also acting on the plow. Friction is directed parallel to the surface and opposes the motion. If the friction force has a magnitude of 625 newtons, what is the work done by friction on the plow?

47. Parallelogram Show that the points $(2, 2, 2)$, $(0, 1, 2)$ , $(-1, 3, 3)$, and $(3, 0, 1)$ are the vertices of a parallelogram.

48. Rectangle Show that the points $(2, 2, 2)$, $(2, 0, 1)$, $(4, 1,-1)$, and $(4, 3, 0)$ are the vertices of a rectangle.

49. Right Triangle Show that the points $(-2, 6, 0)$, $(4, 9, 1)$, and $(-3, 2, 18)$ are the vertices of a right triangle.

50. Right Triangle Find all scalars $c$ so that the triangle with vertices $A=(1,-1,0)$, $B=(-2,2,1)$, and $C=(1,2,c)$ is a right triangle with its right angle at $C$.

51. Work Find the acute angle that a constant unit force vector makes with the positive $x$-axis in moving an object from $(0,0)$ to $(4,0)$ if the work done by the force equals $2$.

52. Work In the definition of work $W=\mathbf{F\,{\cdot}\, \,} \skew5\overrightarrow{\it AB}$, what is the work done if $\mathbf{F}$ is orthogonal to $\skew5\overrightarrow{\it AB}$?

53. Let $\mathbf{u}$ and $\mathbf{w}$ be two unit vectors and let $\theta$ be the angle between them. Find $\left\Vert \dfrac{1}{2}\mathbf{u}- \mathbf{w}\right\Vert$ in terms of $\theta$.

54. Show that the vector projection of $\mathbf{v}$ on $\mathbf{i}$ is $(\mathbf{v}\,{\cdot}\, \mathbf{i})\mathbf{i}$. Then show that a vector $\mathbf{v}$can always be written as $$\begin{equation*} \mathbf{v}=(\mathbf{v}\,{\cdot}\, \mathbf{i})\mathbf{i}+(\mathbf{v}\,{\cdot}\, \mathbf{j})\mathbf{j}+(\mathbf{v}\,{\cdot}\, \mathbf{k})\mathbf{k} \end{equation*}$$

55. If $\Vert \mathbf{v}\Vert \,=2$, $\Vert \mathbf{w}\Vert \,=6$ , and the angle between $\mathbf{v}$ and $\mathbf{w}$ is $\dfrac{\pi }{3}$, find $\Vert \mathbf{v}+\mathbf{w}\Vert$ and $\Vert \mathbf{v}-\mathbf{w} \Vert$.

56. Find all numbers $a$ and $b$ for which the vectors $\mathbf{ v=\,}2a\mathbf{i}-2\mathbf{j}+\mathbf{k}$ and $\mathbf{w}=b\mathbf{i}+2 \mathbf{j}+2\mathbf{k}$ are orthogonal and have the same magnitude.

57. Suppose $\mathbf{v}$and $\mathbf{w}$ are two nonzero vectors. Show that the vector $\mathbf{v}-a\mathbf{w}$ is orthogonal to $\mathbf{w}$ if $a=\dfrac{\mathbf{v}\,{\cdot}\, \mathbf{w}}{\Vert \mathbf{w}\Vert ^{2}}$.

58. Let $\mathbf{v}$ and $\mathbf{w}$ be nonzero vectors. Show that the vectors $\Vert \mathbf{w}\Vert \mathbf{v}+\Vert \mathbf{v}\Vert \mathbf{w }$ and $\Vert \mathbf{w}\Vert \mathbf{v}-\Vert \mathbf{v}\Vert \mathbf{w}$ are orthogonal.

59. Let $\mathbf{w}$ be a nonzero vector and let $\mathbf{u}$ be a unit vector. Show that the unit vector $\mathbf{u}$that makes $\mathbf{w} \,{\cdot}\, \mathbf{u}$ a maximum is the unit vector pointing in the same direction as $\mathbf{w}$.

60. Cauchy–Schwarz Inequality Show that if $\mathbf{v}$ and $\mathbf{w}$ are two vectors, then $\left\vert \mathbf{v}\,{\cdot}\, \mathbf{w} \right\vert \,\leq \left\Vert \mathbf{v}\right\Vert \left\Vert \mathbf{w} \right\Vert$. Under what conditions is the Cauchy–Schwarz inequality an equality?

61. Triangle Inequality Show that if $\mathbf{v}$and $\mathbf{w}$ are vectors, then $\left\Vert \mathbf{v}+\mathbf{w}\right\Vert \leq \left\Vert \mathbf{v}\right\Vert +\left\Vert \mathbf{w}\right\Vert .$ (Hint: Use the Cauchy–Schwarz inequality, Problem 60.)

62. Show that if $\alpha , \beta,$ and $\gamma$ are the direction angles of a nonzero vector $\mathbf{v}$ in space, then $\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =1$.

63. The vector $\mathbf{v}$ makes an angle of $\alpha =\dfrac{\pi }{3}$ with the positive $x$-axis, an angle of $\beta =\dfrac{\pi }{3}$ with the positive $y$-axis, and an acute angle $\gamma$ with the positive $z$ -axis. Find $\gamma$. (Hint: Use the result from Problem 62.)

64. $\left\Vert \mathbf{v}\right\Vert =3$, $\alpha =\dfrac{\pi }{3}$ , $\ \beta =\dfrac{\pi }{4}$, $0 \lt \gamma \lt \dfrac{\pi }{2}$

65. $\left\Vert \mathbf{v}\right\Vert =2$, $\alpha =\dfrac{\pi }{4}$, $\dfrac{ \pi }{2} \lt \beta \lt \pi$, $\gamma =\dfrac{\pi }{3}$

66. $\left\Vert \mathbf{v}\right\Vert =3$, the direction angles are equal, and $\mathbf{v}$ has positive components.

67. $\left\Vert \mathbf{v}\right\Vert =\dfrac{1}{2}$, $\cos \alpha >0$, $\cos \beta =\dfrac{1}{4}$, $\cos \gamma =\sqrt{\dfrac{7}{8}}$

68. Orthogonal Vectors Let $\mathbf{v}=2\mathbf{i}- \mathbf{j}+ \mathbf{k}$ and $\mathbf{w}=4\mathbf{i}+{2}\mathbf{j} -\mathbf{k}$ be two nonzero vectors that are not parallel. Find a vector $\mathbf{u}\neq \mathbf{0}$ that is orthogonal to both $\mathbf{v}$ and $\mathbf{w}$.

69. If $\mathbf{v}$ is a vector for which $\mathbf{v}\,{\cdot}\, \mathbf{i }=0$, $\mathbf{v}\,{\cdot}\, \mathbf{j}=0$, and $\mathbf{v}\,{\cdot}\, \mathbf{k}=0$, find $\mathbf{v}$.

70. Solve for $\mathbf{x}$ in terms of $a$, $\mathbf{a}$, $\mathbf{b }$, and $\mathbf{c}$, if $a\mathbf{x}+(\mathbf{x}\,{\cdot}\, \mathbf{b})\mathbf{a }=\mathbf{c}$, $a\neq 0,$ $a+\mathbf{a}\,{\cdot}\, \mathbf{b}\neq 0$. (Hint: First find $\mathbf{x}\,{\cdot}\, \mathbf{b}$, then $\mathbf{x}$.)

71. Show that:

    1. (a) There is no vector with direction angles $\alpha =\dfrac{\pi }{6}$ and $\beta =\dfrac{\pi }{4}$.
    2. (b) If $\alpha$ and $\beta$ are positive acute direction angles of a vector, then $\alpha +\beta \geq \dfrac{\pi }{2}$.

72. Geometry

    1. (a) Show that the vectors $\mathbf{u}=3\mathbf{i}+ \mathbf{j}-2\mathbf{k}$, $\mathbf{v}=-\mathbf{i}+3\mathbf{j}+4\mathbf{k}$, and $\mathbf{w}=4\mathbf{i}-2\mathbf{j}-6\mathbf{k}$ form the sides of a triangle.
    2. (b) Find the lengths of the medians of the triangle.

73. Suppose $(r, \theta )$ are polar coordinates of a point, where $r\geq 0$. Let $$\mathbf{u}_{r}=(\cos \theta )\,\mathbf{i}+(\sin \theta )\,\mathbf{j}\qquad \mathbf{u}_{\theta }=(-\sin \theta )\,\mathbf{i}+(\cos \theta )\,\mathbf{j}$$

    724

    1. (a) Show that $\mathbf{u}_{r}$ and $\mathbf{u}_{\theta }$ are unit vectors.
    2. (b) Show that $\mathbf{u}_{r}$ and $\mathbf{u}_{\theta }$ are orthogonal.
    3. (c) Show that $\mathbf{u}_{r}$ has the same direction as the ray from the origin to $(r, \theta )$ and that $\mathbf{u}_{\theta }$ is $90^\circ$ counterclockwise from $\mathbf{u}_{r}$.

74. Find an example of three nonzero vectors $\mathbf{a}$ , $\mathbf{b}$ and $\mathbf{c}$ for which $\mathbf{b}\neq \mathbf{c}$, neither $\mathbf{b}$ nor $\mathbf{c}$ is orthogonal to $\mathbf{a}$, and $\mathbf{a}\,{\cdot}\, \mathbf{b}=\mathbf{a}\,{\cdot}\, \mathbf{c}$. Discuss whether there is a Cancellation Property for dot products.

75. If $\theta$ is the angle between the nonzero vectors $\mathbf{v }$ and $\mathbf{w}$, where $0\leq \theta \leq \pi$, show that $$\sin ^{2}\theta =\frac{\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w}\Vert ^{2}-( \mathbf{v}\,{\cdot}\, \mathbf{w})^{2}}{\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w} \Vert ^{2}}$$

76. Let $\theta$ be the angle between the nonzero vectors $\mathbf{ u}=u_{1}\mathbf{i}+u_{2}\mathbf{j}+u_{3}\mathbf{k}$ and $\mathbf{v}=v_{1} \mathbf{i}+v_{2}\mathbf{j}+v_{3}\mathbf{k}$. Show that $$\begin{equation*} \sin ^{2}\theta =\frac{ (u_{2}v_{3}-u_{3}v_{2})^{2}+(u_{1}v_{3}-u_{3}v_{1})^{2}+(u_{1}v_{2}-u_{2}v_{1})^{2} }{\Vert \mathbf{u}\Vert ^{2}\Vert \mathbf{v}\Vert ^{2}} \end{equation*}$$

    (Hint: Begin with $\sin ^{2}\theta =1-\cos ^{2}\theta$.)

77. Suppose that $\mathbf{v}=c_{1}\mathbf{u}_{1}+c_{2}\mathbf{u} _{2}$, where $\mathbf{u}_{1}, \mathbf{u}_{2}$ are nonzero, nonparallel vectors, is a vector in the plane. Find $c_{1}$ and $c_{2}$ in terms of $\mathbf{u}_{1}~$ and $\mathbf{u}_{2}$, and $\mathbf{v}$. What are $c_{1}$ and $c_{2}$ if $\mathbf{u}_{1}$ and $\mathbf{u}_{2}$ are orthogonal unit vectors?

78. Prove the distributive property of the dot product: $\mathbf{ u\,{\cdot}\, }\left( \mathbf{v+w}\right) =\mathbf{u\,{\cdot}\, v+u\,{\cdot}\, w}$ for vectors in the plane and in space.

79. Prove the linearity property: $a\left( \mathbf{u\,{\cdot}\, v}\right) =\left( a\mathbf{u} \right) \,{\cdot}\, \mathbf{v}$, for vectors in the plane and in space.

80. Prove the zero-vector property: $\mathbf{ 0\,{\cdot}\, v=~}0$ for vectors in the plane and in space.

81. Prove the commutative property of the dot product: $\mathbf{ u\,{\cdot}\, v=v\,{\cdot}\, u}$ for vectors in the plane.

82. Prove the magnitude property: $\mathbf{v\,{\cdot}\, v=}\left\Vert \mathbf{v}\right\Vert ^{2}$ for vectors in the plane.

83. The dot product of two vectors $\mathbf{v}=v_{1}\mathbf{e} _{1}+v_{2}\mathbf{e}_{2}+\,{\cdots}\, +v_{n}\mathbf{e}_{n}$ and $\mathbf{w}=w_{1} \mathbf{e}_{1}+w_{2}\mathbf{e}_{2}+\,{\cdots}\, +w_{n}\mathbf{e}_{n}$ in $n$-space is defined as $$\mathbf{v}\,{\cdot}\, \mathbf{w}=v_{1}w_{1}+v_{2}w_{2}+\cdots +v_{n}w_{n}$$

    Show that the five properties of the dot product on p. 716 hold for vectors in $n$-space.

84. Show that $\mathbf{w}=\Vert \mathbf{v}\Vert \mathbf{u}+\Vert \mathbf{u}\Vert \mathbf{v}$ bisects the angle between $\mathbf{u}$ and $\mathbf{v}$.

85. Prove the polarization identity: $\Vert \mathbf{u}+\mathbf{v}\Vert ^{2}-\Vert \mathbf{u}-\mathbf{v}\Vert ^{2}=4( \mathbf{u}\,{\cdot}\, \mathbf{v})$.

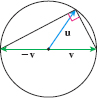
86. 1. (a) If $\mathbf{u}$ and $\mathbf{v}$ are two vectors having the same magnitude, show that $\mathbf{u}+\mathbf{v}$ and $\mathbf{u}- \mathbf{v}$ are orthogonal.
    2. (b) Use this to prove that an angle inscribed in a semicircle is a right angle (see the figure).

    

87. Suppose $\mathbf{v}$ and $\mathbf{w}$ are unit vectors in the plane, making angles $\alpha$ and $\beta ,$ respectively, with the positive $x$-axis.

    1. (a) Show that $\mathbf{v}=(\cos \alpha )\mathbf{i}+(\sin \alpha )\mathbf{j}$ and $\mathbf{w}=(\cos \beta )\mathbf{i}+(\sin \beta )\mathbf{j}$.
    2. (b) Use the dot product $\mathbf{v}\,{\cdot}\, \mathbf{w}$ to prove the sum and difference formulas $$\begin{eqnarray*} \cos (\alpha -\beta )& =&\cos \alpha \cos \beta +\sin \alpha \sin \beta \\ \cos (\alpha +\beta )& =&\cos \alpha \cos \beta -\sin \alpha \sin \beta \end{eqnarray*}$$

88. Gram–Schmidt Orthogonalization Process Let $\mathbf{u}_{1}, \mathbf{u}_{2}$, and $\mathbf{u}_{3}$ be three noncoplanar vectors. Let $\mathbf{w}_{1}=\dfrac{\mathbf{u}_{1}}{\Vert \mathbf{u} _{1}\Vert }$, $\mathbf{v}_{2}=\mathbf{u}_{2}-(\mathbf{u}_{2}\,{\cdot}\, \mathbf{w} _{1})\mathbf{w}_{1}$, $\mathbf{w}_{2}=\dfrac{\mathbf{v}_{2}}{\Vert \mathbf{v} _{2}\Vert }$, $\ \mathbf{v}_{3}=\mathbf{u}_{3}-(\mathbf{u}_{3}\,{\cdot}\, \mathbf{w }_{1})\mathbf{w}_{1}-(\mathbf{u}_{3}\,{\cdot}\, \mathbf{w}_{2})\mathbf{w}_{2}$, and $\mathbf{w}_{3}=\dfrac{\mathbf{v}_{3}}{\Vert \mathbf{v}_{3}\Vert }$. Show that $\mathbf{w}_{1}, \mathbf{w}_{2}$, and $\mathbf{w}_{3}$ are mutually orthogonal unit vectors.

89. Orthogonal Vectors Use the Gram–Schmidt orthogonalization process (Problem 88) to transform $-\mathbf{i}+\mathbf{j}$, $2\mathbf{i}+ \mathbf{k}$, and $3\mathbf{i}-\mathbf{j}+2\mathbf{k}$ into a set of mutually orthogonal unit vectors.

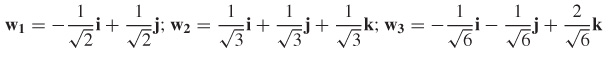
90. Generalize the Gram–Schmidt orthogonalization process (Problem 88) to vectors in $n$ dimensions.

91. Let $\mathbf{u}$ and $\mathbf{v}$ be fixed vectors and define $g(t)=\Vert \mathbf{u}-t\mathbf{v}\Vert ^{2}$. Find the minimum value of $g$ and deduce the Cauchy–Schwarz inequality $\left\vert \mathbf{u}\,{\cdot}\, \mathbf{v}\right\vert \leq \Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert$.

92. Show that two vectors in the plane are parallel if and only if their projections on two fixed mutually orthogonal vectors are proportional.

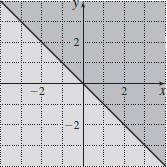
93. Sketch the set of points in the plane with position vector $\mathbf{r}$ satisfying $\mathbf{r}\,{\cdot}\, (\mathbf{i}+\mathbf{j})\geq 0$.

$x+y\geq0$

94. Show that $(\mathbf{r}-\mathbf{b})\,{\cdot}\, (\mathbf{r}+\mathbf{b} )=0$ is a vector equation of the sphere, with $\mathbf{b}$ and $-\mathbf{b}$ as endpoints of a diameter. Show that $(\mathbf{r}-\mathbf{r}_{0}-\mathbf{b} )\,{\cdot}\, (\mathbf{r}-\mathbf{r}_{0}+\mathbf{b})=0$ is a vector equation of the sphere with center $\mathbf{r}_{0}$ and radius $\Vert \mathbf{b} \Vert$.