11.5 Integrals of Vector Functions; Projectile Motion

Up to now we have been given the position function \(\mathbf{r=r}( t) \) of a moving particle, and we have used it to find the particle’s velocity, speed, and acceleration. But in motion problems involving a force applied to an object, we often only know the mass \(m\) of the object and the force vector \(\mathbf{F}\) that is applied to it. By using Newton’s Second Law of Motion, \(\mathbf{F}=m\mathbf{a}\), we can find \(\mathbf{a}\). But to find the motion of the particle, we also need its velocity \(\mathbf{v}\) and its position \(\mathbf{r}\). Since \(\mathbf{a}=\dfrac{d\mathbf{v}}{dt}\) and \(\mathbf{v}=\dfrac{d\mathbf{r}}{dt},\) we can find \(\mathbf{v}\) and then \(\mathbf{r}\) by integrating.

1 Integrate Vector Functions

The integral of a vector function \(\mathbf{r}=\mathbf{r}(t)\) is found by integrating each component individually. That is, if \(\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\), then \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ \int \mathbf{r}(t)dt=\left[ \int x(t)dt\right] \mathbf{i}+\left[ \int y(t)dt\right] \mathbf{j}+\left[ \int z(t)dt\right] \mathbf{k}} \end{equation*}

When integrating a vector function, we must insert a constant of integration into every component. For example, \begin{eqnarray*} \int (\sin t\mathbf{i}+\cos t\mathbf{j}+2\mathbf{k})dt &=& \left( \int \sin t~dt\right) \mathbf{i}+\left( \int \cos t~dt\right) \mathbf{j}+\left( \int 2~dt\right) \mathbf{k}\\ &=&(-\cos t+c_{1})\mathbf{i}+(\sin t+c_{2})\mathbf{j}+(2t+c_{3})\mathbf{k} \end{eqnarray*}

Then using the properties of vector addition, we get \begin{eqnarray*} \int (\sin t\mathbf{i}+\cos t\mathbf{j}+2\mathbf{k})dt&=&-\cos t\mathbf{i }+\sin t\mathbf{j}+2t\mathbf{k}+c_{1}\mathbf{i}+c_{2}\mathbf{j}+c_{3}\mathbf{ k}\\ &=&-\cos t\mathbf{i}+\sin t\mathbf{j}+2t\mathbf{k}+\mathbf{c} \end{eqnarray*}

where \(\mathbf{c}=c_{1}\mathbf{i}\) \(+c_{2}\mathbf{j}\) \(+c_{3}\mathbf{k}\).

2 Solve Projectile Motion Problems

From Newton's Second Law of Motion, \(\mathbf{F}(t)=m\mathbf{a}(t)\). Once we know the force \(\mathbf{F}(t)\) acting on a particle of mass \(m\), the acceleration vector \(\mathbf{a}(t)\) is determined. The velocity vector \( \mathbf{v}(t)\) is the integral of \(\mathbf{a}(t)\). That is, \begin{equation*} \mathbf{v}(t)=\int \mathbf{a}(t)dt \end{equation*}

From this we can find the velocity and speed of the particle, provided an initial condition* on \(\mathbf{v}(t)\) is given. Furthermore, since \begin{equation*} \mathbf{r}(t)=\int \mathbf{v}(t)dt \end{equation*}

we can find the path of the particle if we know an initial condition on \( \mathbf{r}(t)\).

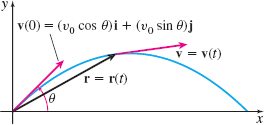
Example 2 is a special case of the projectile problem: Find the path of a projectile fired at an angle \(\theta \) to the horizontal with initial speed \( v_{0},\) assuming that the only force acting on the projectile is gravity. We are interested in knowing the maximum height of the projectile, how far it travels, and how long it is in the air. To simplify the analysis, we choose to start the motion at the origin, so \(\mathbf{r}( 0)\;=\;\mathbf{0.} \) The initial velocity vector \(\mathbf{v}( 0) \) has magnitude \( v_{0}\) and is directed at an inclination \(\theta \) to the horizontal axis, so \(\mathbf{v}( 0)\;=\;v_{0} ( \cos \theta \mathbf{i}+\sin \theta \mathbf{j}) = ( v_{0}\cos \theta)\mathbf{i}+ (v_{0}\sin \theta)\mathbf{j}\).

In Figure 33, \(\mathbf{r}=\mathbf{r}(t)\) represents the position of the projectile after time \(t\) and \(\mathbf{v=v}( t) \) is the velocity vector. We assume the only force acting on the projectile is \(\mathbf{F} =-mg\mathbf{j}\), where \(g\) is the acceleration due to gravity* and \(m\) is the mass of the projectile. From Newton's Second Law of Motion, the acceleration \(\mathbf{a}(t)\) of the projectile obeys \begin{eqnarray*} m\mathbf{a}(t) &=&-mg\mathbf{j} \\[3pt] \mathbf{a}( t) &=&-g\mathbf{j} \end{eqnarray*}

Integrating both sides with respect to \(t\) gives \begin{equation*} \mathbf{v}(t)=\int \mathbf{a}( t) dt=\left( \int -gdt\right) \mathbf{j}=-gt\mathbf{j+c} \end{equation*}

where \(\mathbf{c}\) is a constant vector. When \(t=0\), \(\mathbf{v} (0)=v_{0}\cos \theta \mathbf{i}+v_{0}\sin \theta \mathbf{j=}\) \(\mathbf{c}\). So, the velocity vector of the projectile is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{v}(t)=v_{0}\cos \theta \mathbf{i}+(v_{0}\sin \theta-gt)\mathbf{j}} \end{equation*}

The position of the projectile is given by \begin{equation*} \mathbf{r}(t)=\int \mathbf{v}(t) dt=(v_{0}\cos \theta )t \mathbf{i}+\left[(v_{0}\sin \theta )t-\frac{1}{2}gt^{2}\right]\mathbf{j}+ \mathbf{d} \end{equation*}

where \(\mathbf{d}\) is a constant vector. When \(t=0\), the position of the projectile is at the origin, \(\mathbf{r}( 0)\;=\;\mathbf{0}\), so \( \mathbf{d}=\mathbf{0}\). The position of the projectile at time \(t\) is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{r}(t)=(v_{0}\cos \theta )t\mathbf{i} +\left[(v_{0}\sin \theta )t-\dfrac{1}{2}gt^{2}\right]\mathbf{j}} \end{equation*}

The parametric equations of the motion of the projectile are \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {x=(v_{0}\cos \theta )t\qquad \hbox{and}\qquad y=-\dfrac{1}{2} gt^{2}+(v_{0}\sin \theta )t} \end{equation*}

We use \(t=\dfrac{x}{v_{0}\cos \theta }\) to eliminate \(t\) from these equations. Then the rectangular equation of the motion is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {y=-\dfrac{g}{2v_{0}^{2}\cos ^{2}\theta }x^{2}+x\tan \theta} \end{equation*}

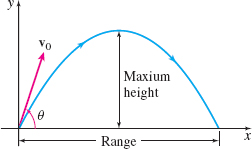
which is the equation of a parabola. See Figure 34.

We are interested in knowing how far the projectile travels horizontally, how long it is in the air, and its maximum height.

The \(x\)-intercepts of the parabola are found by letting \(y=0\). As a result, the \(x\)-intercepts are \begin{equation*} x=0\qquad \hbox{and} \qquad x=\dfrac{2v_{0}^{2}\cos ^{2}\theta \tan \theta }{g}=\dfrac{ v_{0}^{2}\sin ( 2\theta ) }{g} \end{equation*}

The number \(\dfrac{v_{0}^{2}\sin ( 2\theta ) }{g}\), called the range of the projectile, tells us the horizontal distance the projectile travels. In Problem 39, you are asked to show that an inclination of \(\theta\;=\;\dfrac{\pi }{4}\) gives the maximum range.

The projectile hits the ground when \(y=0\) and \(t>0\). We use the parametric equation of the motion for \(y\), let \(y=0\), and solve for \(t.\) \begin{eqnarray*} y&\;=\;&-\frac{1}{2}gt^{2}+(v_{0}\sin \theta )t \\[6pt] 0&\;=\;&-\frac{1}{2}gt^{2}+(v_{0}\sin \theta )t\hbox{ } \\[6pt] \frac{1}{2}gt&\;=\;&v_{0}\sin \theta \\[6pt] t&\;=\;&\frac{2v_{0}\sin \theta }{g} \end{eqnarray*}

The projectile is in the air for \(\dfrac{2v_{0}\sin \theta }{g}\) seconds.

The projectile reaches its maximum height when \(\dfrac{dy}{dt}\;=\;-gt+v_{0}\sin \theta\;=\;0.\) The maximum height is reached at \(t= \dfrac{v_{0}\sin \theta }{g}\) seconds. The maximum height is \begin{equation*} y=-\frac{1}{2}g\!\left( \frac{v_{0}^{2}\sin ^{2}\theta }{g^{2}}\right) +( v_{0}\sin \theta ) \!\left( \frac{v_{0}\sin \theta }{g}\right)\;=\;\frac{ v_{0}^{2}\sin ^{2}\theta }{2g} \end{equation*}

The formulas for the range of a projectile and its maximum height derived here are valid only for the initial conditions specified by \(\mathbf{r} (0)\;=\;\mathbf{0}\) and \(\mathbf{v}(0)=v_{0}\cos \theta \mathbf{i} +v_{0}\sin \theta \mathbf{j}\). If different initial conditions are given, the range and maximum height of the projectile will be different. In such instances, merely follow the same pattern of solution, adjusting where needed for different initial conditions.