14.2 Assess Your UnderstandingPrinted Page 920
920
Concepts and Vocabulary
A closed, bounded region R that has a boundary consisting of two smooth curves, y=g1(x) and y=g2(x), defined on a≤x≤b, where g1(x)≤g2(x) on [a,b] and possibly a portion of the vertical lines x=a and x=b, is called a(n) ________ region.
x-simple region
True or False The double integral of a function that is continuous on a closed, bounded, y-simple region R can be expressed as an iterated integral.
True
True or False The region R enclosed by the parabola y=x2+1 and the line y=3x+1 is both x-simple and y-simple.
True
Explain why ∫10[∫x0f(x,y)dy]dx≠∫10[∫y0f(x,y)dx]dy.
Answers will vary.
Skill Building
In Problems 5–8, express ∬ as an iterated integral in two ways:
- (a) one with the integration with respect to x first;
- (b) the other with the integration with respect to y first,
- (c) find each double integral over the region R.
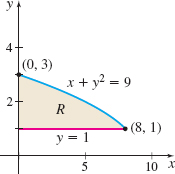
- (a) \int_1^3 \left[\int_0^{9-y^2} x y^2 \, dx \right]\;dy
- (b) \int_0^8 \left[\int_1^{\sqrt{9-x}} x y^2 \, dy\right]\;dx
- (c) \dfrac{2504}{35}
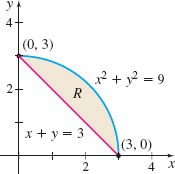
- (a) \int_0^3 \Big[ \int_{3-y}^{\sqrt{9-y^2}} x y^2\, dx\Big]\;dy
- (b) \int_0^3 \Big[\int_{3-x}^{\sqrt{9-x^2}} x y^2 \, dy\Big]\;dx
- (c) \dfrac{243}{20}
In Problems 9–24, find each iterated integral. Identify and graph the region R associated with each integral.
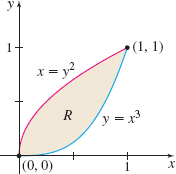
\displaystyle\int_{0}^{1}\left[ \int_{x^{2}}^{\sqrt{x}}\,{\it dy}\right]\! {\it dx}
\dfrac13
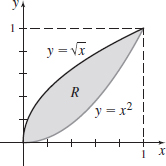
\displaystyle\int_{0}^{1}\left[ \int_{y^{2}}^{\sqrt{y}}x\,{\it dx}\right]\! {\it dy}
\displaystyle\int_{-1}^{2}\left[\int_{y^{2}}^{y+2}\,{\it dx}\right]\! {\it dy}
\dfrac92
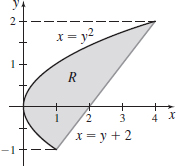
\displaystyle\int_{0}^{1}\left[ \int_{x}^{2x}y\,{\it dy}\right]\! {\it dx}
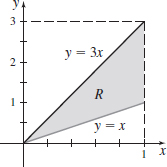
\displaystyle\int_{0}^{1}\left[ \int_{x}^{3x}xy\,{\it dy}\right]\! {\it dx}
1
\displaystyle\int_{0}^{1}\left[ \int_{y}^{\sqrt{y}}x^{2}y\,{\it dx}\right]\! {\it dy}
\int_{0}^{1}\left[ \int_{1}^{e^{y}}\dfrac{y}{x}\,{\it dx}\right]\! {\it dy}
\dfrac13
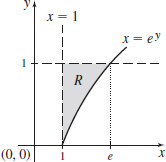
\int_{0}^{1}\left[\int_{0}^{x^{2}}xe^{y}\,{\it dy}\right]\! {\it dx}
\int_{0}^{2}\left[ \int_{y}^{2y}xy\,{\it dx}\right]\! {\it dy}
6
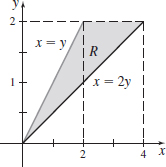
\int_{2}^{4}\left[ \int_{1}^{y^{2}}\dfrac{y}{x^{2}}\,{\it dx}\right]\! {\it dy}
\int_{0}^{1}\left[ \int_{x^{2}}^{x}\sqrt{xy}\,{\it dy}\right]\! {\it dx}
\dfrac2{27}
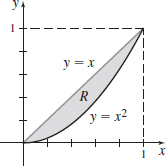
\int_{0}^{1}\left[\int_{x^{2}}^{x}\sqrt{x}\,{\it dy}\right]\! {\it dx}
\int_{0}^{1}\left[ \int_{x}^{1}\dfrac{1}{x^{2}+1}\,{\it dy}\right]\! {\it dx}
\dfrac{\pi}4 - \dfrac{\ln 2}2
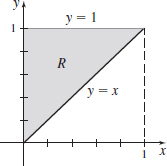
\int_{0}^{1}\left[ \int_{y}^{\sqrt{y}}(x^{2}+y^{2})\,{\it dx}\right]\! {\it dy}
\int_{1}^{2}\left[ \int_{0}^{\ln x}xe^{y}\,{\it dy}\right]\! {\it dx}
\dfrac56
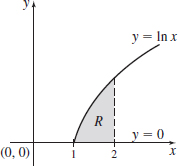
\int_{2}^{3}\left[ \int_{0}^{1/y}\ln y\,{\it dx}\right]\! {\it dy}
In Problems 25–28, find each double integral. Start by graphing the region R. Pay particular attention to the boundary, since it determines the correct limits of integration.
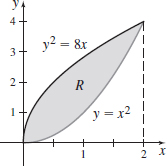
\displaystyle\iint\limits_{\kern-3ptR}(x+y)\,{\it dA}, where R is the region enclosed by y=x^{2} and y^{2}=8x
\dfrac{36}5
\displaystyle\iint\limits_{\kern-3ptR}(x^{2}-y^{2})\,{\it dA}, where R is the region enclosed by y=x and y=x^{2}
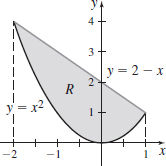
\displaystyle\iint\limits_{\kern-3ptR}y^{2}\,{\it dA}, where R is the region enclosed by y=2-x and y=x^{2}
\dfrac{423}{28}
\displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA}, where R is the region enclosed by y^{2}=x+1 and y=1-x
In Problems 29–36, use double integration to find the area of each region.
Enclosed by the graphs of y=x^{3} and y=x^{2}
A = \dfrac1{12} square units
Enclosed by the graphs of y=2 \sqrt{x} and y=\dfrac{x^{2}}{4}
Enclosed by the graphs of y=x^{2}-9 and y=9-x^{2}
A = 72 square units
Enclosed by the graphs of x^{2}+y^{2}=16 and y^{2}=6x
Enclosed by the graph y=\dfrac{1}{\sqrt{x-1}}, the x -axis, and the lines x=2 and x=5
A = 2 square units
Enclosed by the graphs of y=x^{3/2} and y=x
Enclosed by the line x+y=3 and the hyperbola xy=2
A = \dfrac32 - 2\;\ln\;2 square units
Enclosed by the hyperbola xy=\sqrt{3} and the circle x^{2}+y^{2}=4, in the first quadrant only
In Problems 37–44, change the order of integration of each iterated integral to obtain an equivalent expression.
\int_{0}^{1}\left[ \int_{0}^{x}f(x,y)\,{\it dy}\right]\! {\it dx}
\int_0^1 \left[ \int_y^1 f(x,y) \, dx\right]\;dy
\int_{0}^{2}\left[ \int_{y^{2}}^{2y}f(x,y)\,{\it dx}\right]\! {\it dy}
\int_{0}^{a}\left[ \int_{0}^{\sqrt{a^{2}-y^{2}}}f(x,y)\,{\it dx}\right]\! {\it dy}
\int_0^a \Big[ \int_0^{\sqrt{a^2-x^2}} f(x,y)\, dy\Big]\;dx
921
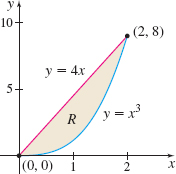
\int_{0}^{2\sqrt[3]{2}}\left[ \int_{x^{2}/4}^{\sqrt{x}}f(x,y)\,{\it dy}\right]\! {\it dx}
\int_{0}^{16}\left[\int^{y^{1/4}}_{y/8} f(x,y)\,{\it dx}\right]\! {\it dy}
\int_0^2 \left[ \int_{x^4}^{8x} f(x,y) \, dy\right]\;dx
\int_{2}^{5}\left[ \int_{x^{2}-6x+9}^{x-1}f(x,y)\,{\it dy}\right]\! {\it dx}
\int_{1}^{2}\left[ \int_{0}^{\ln y}f(x,y)\,{\it dx}\right]\! {\it dy}
\int_0^{\ln 2} \left[ \int_{e^x}^2 f(x,y)\, dy\right]\;dx
\int_{1}^{e}\left[ \int_{\ln x}^{1}f(x,y)\,{\it dy} \right]\! {\it dx}
In Problems 45–48, the functions f and g are continuous on a closed, bounded region R, \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\, {\it dA}=8 and \displaystyle\iint\limits_{\kern-3ptR}g(x,y)\, {\it dA}=-6. Use properties of double integrals to find each double integral.
\displaystyle\iint\limits_{\kern-3ptR}[ f(x,y) -g(x,y) ] \, {\it dA}
14
\displaystyle\iint\limits_{\kern-3ptR}4f(x,y) \, {\it dA}
\displaystyle\iint\limits_{\kern-3ptR}[ 3f(x,y) +4g(x,y) ] \, {\it dA}
0
\displaystyle\iint\limits_{\kern-3ptR} [ 2f(x,y) +5g(x,y) ] \, {\it dA}
Applications and Extensions
Area Find the area of the region R in the first quadrant enclosed by the graphs of y=6x-x^{2} and y=4x-8 by partitioning R with a horizontal line through the point (4,8). Refer to Figure 20.
A = \dfrac{56}3 square units
Area Use double integration to find the area in the first quadrant enclosed by the parabola x^{2}=9y, the y-axis, and the circle x^{2}+y^{2}=10.
Volume In Problems 51–60, find the volume of each solid.
The tetrahedron enclosed by the plane x+2y+z=2 and the coordinate planes
V= \dfrac23 cubic units
Enclosed by the elliptic paraboloid 4x^{2}+9y^{2}=36 and the planes z=0 and z=1
Below the paraboloid z=x^{2}+y^{2} and above the triangular region R formed by the x- and y-axes and the line x+y=1, as shown in the figure below.
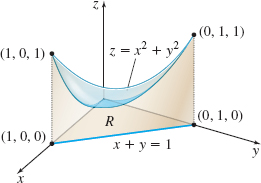
V=\dfrac16 cubic units
Enclosed by the cylinder z=9-y^{2} and the planes x=0, x=4, and z=0
Enclosed by the surface z=4-x^{2}-y^{2} and z=0
V=8 \pi cubic units
Enclosed by the surfaces x^{2}+y^{2}=1, z=x, and z=x^{2}
The solid bounded from above by the graph of z=x^{2}+y^{2}, from below by the xy-plane, and on the sides by the cylinder x^{2}+y^{2}=1, as shown in the figure.
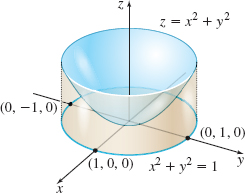
V=\dfrac{\pi}2 cubic units
Enclosed by a portion of the parabolic cylinder z=\dfrac{x^{2} }{2} and the four planes y=0, y=x, x=2, and z=0
Enclosed by the coordinate planes, the plane y=3, and the surface z=y+1-x^{2}
V=\dfrac{124}{15} cubic units
Enclosed by the surfaces z=xe^{y}, z=0, y=0, x=1, and y=x^{2}
In Problems 61–68. (a) graph the region associated with each iterated integral, (b) reverse the order of integration, and (c) find the new iterated integral.
\int_{0}^{\sqrt{\pi /2}}\left[ \int_{y}^{\sqrt{\pi /2}}\sin x^{2}\,{\it dx}\right]\! {\it dy}
- (a)
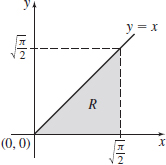
- (b) \int_0^{\sqrt{\pi/2}} \left[ \int_0^x\;\sin\;x^2 \, dy\right]\;dx
- (c) \dfrac12
\int_{0}^{1/2}\left[ \int_{2x}^{1}e^{y^{2}} {\it dy}\right]\! {\it dx}
\int_{0}^{1}\left[ \int_{0}^{\sqrt{1-x^{2}}}\dfrac{1}{\sqrt{1-y^{2}}}\,{\it dy}\right]\! {\it dx}
- (a)
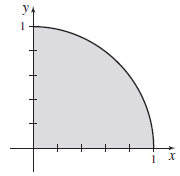
- (b) \int_0^1 \left[ \int_0^{\sqrt{1-y^2}} \dfrac{1}{\sqrt{1-y^2}} \, dx\right]\;dy
- (c) 1
\int_{0}^{1}\left[ \int_{y}^{1}\dfrac{\sin x}{x}\,{\it dx}\right]{\it dy}
\int_{0}^{1}\left[ \int_{y}^{1}\sqrt{2+x^{2}}\,{\it dx}\right]\! {\it dy}
- (a)
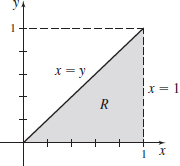
- (b) \int_0^1 \left[ \int_0^x \sqrt{2+x^2} \, dy \right] dx
- (c) \sqrt{3} - \dfrac{2 \sqrt{2}}3
\int_{0}^{1}\left[ \int_{\sqrt[3]{x}}^{1}\sqrt{1+y^{4}}~{\it dy}\right]\! {\it dx}
\int_{0}^{1}\left[ \int_{\sqrt{y}}^{1}e^{y/x}\,{\it dx}\right]\! {\it dy}
- (a)
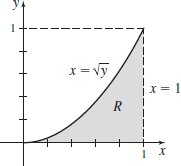
- (b) \int_0^1 \left[ \int_0^{x^2} e^{y/x} \, dy\right]\;dx
- (c) \dfrac12
\int_{0}^{1}\left[ \int_{\sin ^{-1}y}^{\pi /2}e^{\cos x}\,{\it dx}\right]\! {\it dy}
Properties of Double Integrals Let R be the region enclosed by y=1, y=-1, x=0, and x=1; let R_{1} and R_{2} be the subregions of R in the first and fourth quadrants, respectively. Suppose f is continuous on R and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR}3f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=\displaystyle\iint \limits_{\kern-3ptR_{2}}f(x,y)\,{\it dA}, \\[3pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}5f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=18 \end{eqnarray*}
Find \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}.
\iint\limits_{\hspace{-3pt}R\hspace{3pt}} f(x,y) \, dA = -2
Properties of Double Integrals Let R be the region enclosed by y=0, y=2, x=-2, and x=1; let R_{1} and R_{2} be the subregions of R in the first and second quadrants, respectively. Suppose f is continuous on R and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR_{2}}3f(x,y)\,{\it dA}-\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=2\displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA},\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{1}}4f(x,y)\,{\it dA}+\displaystyle\iint\limits_{\kern-3ptR_{2}}2f(x,y)\,{\it dA}=7 \end{eqnarray*}
Find \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}.
922
Properties of Double Integrals Let R be the region enclosed by y=x, y=-1, and x=2; let R_{1} and R_{2} be the subregions of R above the x-axis and below the x-axis, respectively. Suppose f is continuous on R and \begin{eqnarray*} &&2\displaystyle\iint\limits_{\kern-3ptR_2}f(x,y)\,{\it dA}-7\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=17\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}f(x,y)\,{\it dA}-2\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=7 \end{eqnarray*}
Find \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}.
\iint\limits_{\hspace{-3pt}R\hspace{3pt}} f(x,y) \, dA = 4.
Properties of Double Integrals Let R be the region enclosed by y=x^{2}+1, y=0, x=-1, and x=2; let R_{1} and R_{2} be the subregions of R in the first and second quadrants, respectively. Suppose f is continuous on R and \begin{eqnarray*} &&\displaystyle\iint\limits_{\kern-3ptR_2}6f(x,y)\,{\it dA}-3\displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA}=-12\\[4pt] &&\displaystyle\iint\limits_{\kern-3ptR_{2}}4f(x,y)\,{\it dA}+2= \displaystyle\iint\limits_{\kern-3ptR_{1}}f(x,y)\,{\it dA} \end{eqnarray*}
Find \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}.
In Problems 73–76, each of the iterated integrals represents the volume of a solid. Describe the solid.
\int_{0}^{1}\left[ \int_{0}^{\sqrt{1-x^{2}}}\sqrt{1-x^{2}-y^2}\,{\it dy}\right]\! {\it dx}
The solid is the volume under the hemisphere z=\sqrt{1-x^2-y^2} in the first octant.
\int_{0}^{2}\left[ \int_{0}^{\sqrt{4-y^{2}}}(4-x^2-y^2)\,{\it dx}\right]\! {\it dy}
\int_{0}^{4}\left[ \int_{0}^{1}3\,{\it dy}\right]\! {\it dx}
The solid is a rectangular box with height z=3 units, with a rectangular base of dimensions x=4 units and y = 1 unit.
\int_{0}^{1}\left[ \int_{0}^{2}2\,{\it dy}\right]\! {\it dx}
Find:
- (a) \displaystyle\iint\limits_{\kern-3ptR}x\,{\it dA}, where R is the region enclosed by the circle of radius 1 centered at the origin.
- (b) 4\displaystyle\iint\limits_{\kern-3ptR_{1}}x\,{\it dA}, where R_{1} is the region in the first quadrant enclosed by the circle of radius 1 centered at the origin (This shows that although the region over which we are integrating is symmetric about the x-axis and the y-axis, we must also consider properties of the integrand on this region before we use symmetry.)
- (a) 0
- (b) \dfrac43
- (a) Find \int_{1}^{e}\left[ \int_{0}^{\ln x}\dfrac{{\it dy}}{x}\right]\! {\it dx}.
- (b) Reverse the order of integration and find the resulting iterated integral.
- (a) Find \int_{0}^{\pi /2}\left[ \int_{0}^{\cos x}\sin x\,{\it dy}\right]\! {\it dx}.
- (b) Reverse the order of integration and find the resulting iterated integral.
- (a) \dfrac12
- (b) \int_0^1 \left[ \int_0^{\cos^{-1}y} \sin\;x \, dx \right]\;dy=\dfrac12
Volume of a Liquid A tank in the shape of a half-cylinder is lying on its flat side. The radius of the tank is 1 m and its length is 4 m. If the tank is filled with liquid to a depth of a meters, what is the volume of the liquid? (Hint: Position the half cylinder as shown in the figure below.)
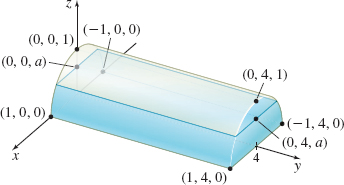
Volume of a Liquid Repeat Problem 80 if the tank is buried so its rounded base is 1 m under the ground and its flat side is at ground level. See the figure below.
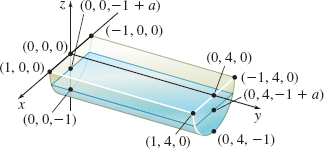
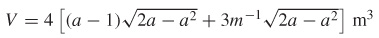
Damming a Valley A dam is built in a V-shaped valley. The top of the dam is 200 m wide and the lowest point in the V is 150 m below the top, as shown in the figure. The pressure P due to the water at a depth d meters below the surface is P=\rho gd, where \rho =1000 \text{kg}/ \text{m}^{3} and g=9.8 \text{m}/ {\text s}^{2}. What is the total outward force F from the water that this dam must be able to withstand? Express your answer in both newtons and pounds using the fact that 1 {\text N} \approx 0.2248 \text{lb}. (Recall that pressure is P=\dfrac{F}{A}, so the force F=PA.)
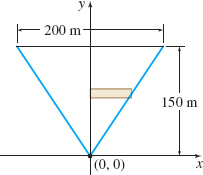
Explain if the following equality is true or false without finding the exact value of the two integrals: \int_{-3}^{3}\int_{-\sqrt{ 9-y^{2}}}^{\sqrt{9-y^{2}}} ( 7-x)\,{\it dx}\, {\it dy}=4\int_{0}^{3}\int_{0}^{ \sqrt{9-y^{2}}}( 7-x)\,{\it dx}\, {\it dy}
Answers will vary.
Volume Find the volume of the tetrahedron enclosed by the coordinate planes and the plane \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1. (Assume that a,b, and c are positive.)
Find \displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA}, where R is the region enclosed by y=4-x^{2} and y=x^{2} to the right of the y-axis.
4
Find \displaystyle\iint\limits_{\kern-3ptR}xy\,{\it dA}, where R is the region enclosed by x=4-y^{2} and x=y^{2} above the x-axis.
Find \displaystyle\iint\limits_{\kern-3ptR}e^{\sqrt{x}}\,{\it dA}, where R is the dregion enclosed by y=x, x=1, y=0.
12 - 4e
923
- (a) Graph the region R defined by 0\leq a\leq y\leq b, 0\leq a\leq x\leq y.
- (b) If z=f(x) is continuous on R, show that \displaystyle\iint\limits_{\kern-3ptR}f(x) \,{\it dA}=\int_{a}^{b}(b-x)f(x)\,{\it dx}.
Properties of Double Integrals Using properties of double integrals, show that if the functions f and g are integrable on R and f(x,y)\leq g(x,y) for all (x,y) in R, then \displaystyle\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA} \leq \displaystyle\iint\limits_{\kern-3ptR}g(x,y)\,{\it dA}.
See the Student Solutions Manual.
Challenge Problem
Volume Find the volume of the solid under the graph of the elliptic paraboloid z=8-2x^{2}-y^{2} and above the first quadrant of the xy-plane. (Hint: Use Wallis’s formula from Section 7.1, Problem 69.)