15.1 Assess Your UnderstandingPrinted Page 976
Concepts and Vocabulary
A(n) _____ _______ is a function that associates a vector to a point in the plane or to a point in space.
Vector field
True or False Let P=P(x,y,z), Q=Q(x,y,z), and R=R(x,y,z) be functions of three variables defined on a subset E of space. A vector field over E is defined as the function F(x,y,z)=P(x,y,z)+Q(x,y,z)+R(x,y,z).
False
The domain of the vector field F=F(x,y) is a set of points (x,y) in the plane, and the range of F is a set of ______ in the plane.
Vectors
977
True or False The gradient of a function f is an example of a vector field.
True
Skill Building
In Problems 5–14, describe each vector field by drawing some of its vectors.
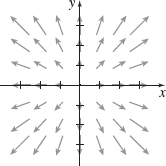
F=F(x,y)=xi+yj
The vector field is pictured below. See the Student Solutions Manual for a description.
F=F(x,y)=xi−yj
F=F(x,y)=i+xj
The vector field is pictured below. See the Student Solutions Manual for a description.

F=F(x,y)=yi−j
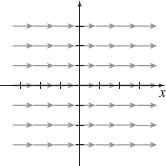
F=F(x,y)=i
The vector field is pictured below. See the Student Solutions Manual for a description.
F=F(x,y)=−j
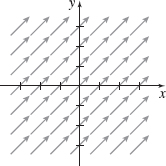
F=F(x,y)=i+j
The vector field is pictured below. See the Student Solutions Manual for a description.
F=F(x,y)=−i+j
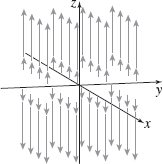
F=F(x,y,z)=zk
The vector field is pictured below. See the Student Solutions Manual for a description.
F=F(x,y,z)=xi
![]() In Problems 15 and 16, use graphing technology to represent each vector field. Then describe the vector field.
In Problems 15 and 16, use graphing technology to represent each vector field. Then describe the vector field.
F=F(x,y,z)=xi+yj+zk√x2+y2+z2
The vector field is pictured below. See the Student Solutions Manual for a description.
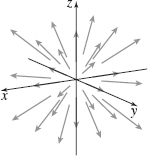
F=F(x,y,z)=−xi+yj+zk√x2+y2+z2
Applications and Extensions
In Problems 17–20, find the gradient vector field of each function f.
f(x,y)=xsiny+cosy
∇f(x,y)=sinyi+(xcosy−siny)j
f(x,y)=xey
f(x,y,z)=x2y+xy+y2z
∇f(x,y,z)=(2xy+y)i+(x2+x+2yz)j+y2k
f(x,y,z)=x2y+xyz2
- (a) Show that the vector field from Example 1, F=F(x,y)=−yi+xj, is a set of vectors tangent to circles centered at the origin.
- (b) Confirm that the magnitude of each vector equals the radius of the circle.
See Student Solutions Manual.
Gravitational Potential Energy The gravitational field g due to a very small object of mass mkg that is r meters (m) from a large object is given by g=−Gmr3r, where G=6.67×10−11Nm2/kg2 and r=xi+yj+zk. Show that the gravitational field is a gradient vector field. That is, show that \mathbf{g}=- {\boldsymbol\nabla }u, where u=-\dfrac{Gm}{r}. The scalar function u is called the gravitational potential due to the mass m.
