The Derivative

2.2 Assess Your Understanding
Printed Page 160

Concepts and Vocabulary

True or False The domain of a function $f$ and the domain of its derivative function $f^\prime$ are always equal.

False

True or False If a function is continuous at a number $c$ , then it is differentiable at $c$ .

False

Multiple Choice If $f$ is continuous at a number $c$ and if $\lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c}$ is infinite, then the graph of $f$ has [(a) a horizontal, (b) a vertical, (c) no] tangent line at $c$ .

(b) Vertical

The instruction “Differentiate $f$ ” means to find the ____ of $f$ .

derivative

Skill Building

In Problems 5–10, find the rate of change of each function f at any real number $c.$

$f(x)=10$

$f(x)=-4$

$f(x)=2x+3$

$f(x)=3x-5$

$f(x)=2-x^{2}$

$-2c$

$f(x)=2x^{2}+4$

In Problems 11–16, differentiate each function f and determine the domain of $f^\prime$ . Use form (3) on page 154.

$f(x)=5$

$f'(x)=0$ , all real numbers

$f(x)=-2$

$f(x)=3x^{2}+x+5$

$f'(x)=6x+1$ , all real numbers

$f(x)=2x^{2}-x-7$

$f(x)=5 \sqrt{x-1}$

$f'(x)=\dfrac{5}{2\sqrt{x-1}}$ , $x\,{>}\,1$

$f(x)= 4\sqrt{x+3}$

In Problems 17–22, differentiate each function $f$ . Graph $y=f( x)$ and $y=f^\prime ( x)$ on the same set of coordinate axes.

$f(x)=\dfrac{1}{3}x+1$

$f'(x)=\dfrac{1}{3}$

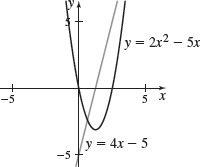
$f(x)=-4x-5$

$f(x)=2x^{2}-5x$

$f'(x)=4x-5$

$f(x)=-3x^{2}+2$

$f(x)=x^{3}-8x$

$f'(x)=3x^{2}-8$

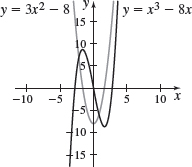
$f(x)=-x^{3}-8$

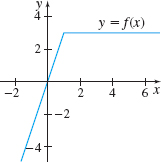
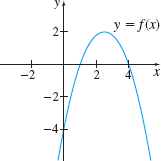
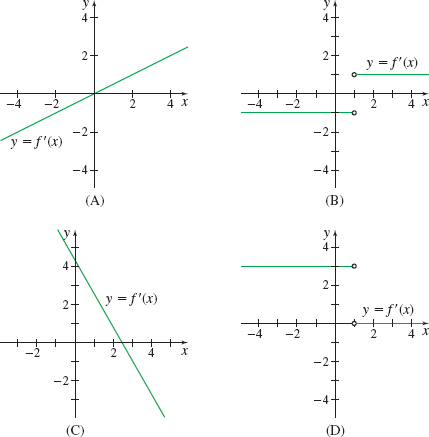
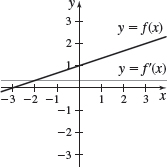
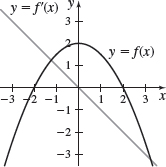
In Problems 23–26, for each figure determine if the graphs represent a function f and its derivative $f^\prime$ . If they do, indicate which is the graph of f and which is the graph of $f^\prime$ .

Not a graph of $f$ and $f'$

Graph of $f$ and $f'$ . The black curve is the graph of $f$ ; the gray curve is the graph of $f'$ .

In Problems 27–30, use the graph of f to obtain the graph of $f^\prime$ .

In Problems 31–34, the graph of a function f is given. Match each graph to the graph of its derivative $f^\prime$ in A–D.

(B)

161

(A)

In Problems 35–44, determine whether each function f has a derivative at c. If it does, what is $f^\prime ( c) ?$ If it does not, give the reason why.

$f( x) =x^{2/3}$ at $c=-8$

$f'(-8)=-\dfrac{1}{3}$

$f( x) =2x^{1/3}$ at $c=0$

$f(x)=|x^{2}-4|$ at $c=2$

$f'(2)$ does not exist.

$f(x)=\vert x^{2}-4|$ at $c=-2$

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} 2x+3 &\hbox{if} & x < 1 \\ x^{2}+4 &\hbox{if} & x ≥ 1 \end{array} } &\hbox{at} & c=1 \end{array} \right.$

$f'(1)=2$

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} 3-4x &\hbox{if} & x < -1 \\ 2x+9 &\hbox{if} & x ≥ -1 \end{array} } &\hbox{at} & c=-1 \end{array} \right.$

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} -4+2x &\hbox{if} & x ≤ \dfrac{1}{2} \\ 4x^{2}-4 &\hbox{if} & x > \dfrac{1}{2} \end{array} } &\hbox{at} & c=\dfrac{1}{2} \end{array} \right.$

$f'\left(\dfrac{1}{2}\right)$ does not exist.

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} 2x^{2}+1 &\hbox{if} & x < -1 \\[3pt] -1-4x &\hbox{if} & x ≥ -1 \end{array} } &\hbox{at} & c=-1 \end{array} \right.$

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} 2x^{2}+1 &\hbox{if} & x < -1 \\[3pt] 2+2x &\hbox{if} & x ≥ -1 \end{array} } &\hbox{at} & c=-1 \end{array} \right.$

$f'(-1)$ does not exist.

$f(x)=\left\{ \begin{array}{@{}l@{\quad}l} {\ \begin{array}{@{}l@{\quad}ll} 5-2x &\hbox{if} & x < 2 \\ x^{2} &\hbox{if} & x ≥ 2 \end{array} } &\hbox{at} & c=2 \end{array} \right.$

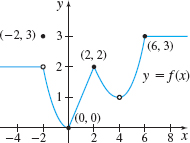
In Problems 45 and 46, use the given points $(c, f(c))$ on the graph of the function f.

(a) For which numbers c does $\lim\limits_{x\rightarrow c}f(x)$ exist but $f$ is not continuous at $c$ ?
(b) For which numbers c is f continuous at c but not differentiable at c?

$-2$ and 4
(b) 0, 2, 6

Heaviside Functions In Problems 47 and 48:

(a) Determine if the given Heaviside function is differentiable at $c$ .
(b) Give a physical interpretation of each function.

$u_{1}( t) =\left\{ \begin{array}{l@{\quad}ll} 0 &\hbox{if} & t < 1 \\ 1 &\hbox{if} & t ≥ 1 \end{array} \right.$ at $c=1$

$u_{1}'(1)$ does not exist.
$u_{1}(t)$ models a switch that is off when $t<1$ and on when $t\geq 1$ .

$u_{3}( t) =\left\{ \begin{array}{l@{\quad}ll} 0 &\hbox{if} & t < 3 \\ 1 &\hbox{if} & t ≥ 3 \end{array} \right.$ at $c=3$

In Problems 49–52, find the derivative of each function.

$f(x)=mx+b$

$f'(x)=m$

$f(x)=ax^{2}+bx+c$

$f(x)=\dfrac{1}{x^{2}}$

$f'(x)=-2/x^{3}$

$f(x)=\dfrac{1}{\sqrt{x}}$

Applications and Extensions

In Problems 53–60, each limit represents the derivative of a function f at some number c. Determine f and c in each case.

${\lim\limits_{h\rightarrow 0}\dfrac{(2+h)^{2}-4}{h} }$

$f(x)=x^{2}$ , $c=2$

${\lim\limits_{h\rightarrow 0}\dfrac{(2+h)^{3}-8}{h} }$

${\lim\limits_{x\rightarrow 1}\dfrac{x^{2}-1}{x-1}}$

$f(x)=x^{2}$ , $c=1$

${\lim\limits_{x\rightarrow 1}\dfrac{x^{14}-1}{x-1}}$

${\lim\limits_{x\rightarrow {\pi /6}}\dfrac{\sin x- \dfrac{1}{2}}{x-\dfrac{\pi }{6}}}$

$f(x)=\sin x$ , $c=\dfrac{\pi}{6}$

${ \lim\limits_{x\rightarrow {\pi /4}}\dfrac{\cos x-\dfrac{\sqrt{2}}{2}}{ x-\dfrac{\pi }{4}}}$

${\lim\limits_{x\rightarrow 0}\dfrac{2(x+2)^{2}-(x+2)-6}{x}}$

$f(x)=2(x+2)^2 -(x+2),c=0$

${\lim\limits_{x \rightarrow 0}\dfrac{3x^{3}-2x}{x}}$

For the function $f(x)=\left\{ \begin{array}{l@{\quad}ll} x^{3} &\hbox{if} & x ≤ 0 \\ x^{2} &\hbox{if} & x>0 \end{array} \right.$ , determine whether:
1. $f$ is continuous at 0.
2. $f^\prime (0)$ exists.
3. Graph the function $f$ and its derivative $f^\prime .$

(a) Continuous at 0
$f'(0)=0$
(c)

162

For the function $f(x)=\left\{ \begin{array}{l@{\quad}ll} 2x &\hbox{if} & x ≤ 0 \\ x^{2} &\hbox{if} & x>0 \end{array} \right.$ , determine whether:
1. $f$ is continuous at 0.
2. $f^\prime (0)$ exists.
3. Graph the function $f$ and its derivative $f^\prime .$

Velocity The distance $s$ (in feet) of an automobile from the origin at time $t$ (in seconds) is given by $s=s( t) =\left\{ \begin{array}{l@{\quad}ll} t^{3} &\hbox{if} & 0 ≤ t < 5 \\ 125 &\hbox{if} & t ≥ 5 \end{array} \right.$ (This could represent a crash test in which a vehicle is accelerated until it hits a brick wall at $t=5{s}$ .)
1. Find the velocity just before impact (at $t=4.99{s}$ ) and just after impact (at $t=5.01{s})$ .
2. Is the velocity function $v=s\prime ( t)$ continuous at $t=5?$
3. (c) How do you interpret the answer to (b)?

$s'(4.99)=74.7003$ ft/s; $s'(5.01)=0$ ft/s
(b) Not continuous
(c) Answers will vary.

Population Growth A simple model for population growth states that the rate of change of population size $P$ with respect to time $t$ is proportional to the population size. Express this statement as an equation involving a derivative.

Atmospheric Pressure Atmospheric pressure $p$ decreases as the distance $x$ from the surface of Earth increases, and the rate of change of pressure with respect to altitude is proportional to the pressure. Express this law as an equation involving a derivative.

$\dfrac{dp}{dx}=-kp$ , $k>0$ .

Electrical Current Under certain conditions, an electric current $I$ will die out at a rate (with respect to time $t$ ) that is proportional to the current remaining. Express this law as an equation involving a derivative.

Tangent Line Let $f(x)=x^{2}+2$ . Find all points on the graph of $f$ for which the tangent line passes through the origin.

$(\sqrt{2},4)$ and $(-\sqrt{2},4)$

Tangent Line Let $f(x)=x^{2}-2x+1$ . Find all points on the graph of $f$ for which the tangent line passes through the point $(1,-1)$ .

Area and Circumference of a Circle A circle of radius $r$ has area $A=\pi r^{2}$ and circumference $C=2\pi r.$ If the radius changes from $r$ to $r + \Delta r$ , find the:
1. (a) Change in area
2. (b) Change in circumference
3. (c) Average rate of change of area with respect to radius
4. (d) Average rate of change of circumference with respect to radius
5. (e) Rate of change of circumference with respect to radius

$2\pi r(\Delta r)+\pi (\Delta r)^2$
$2\pi \Delta r$
$2\pi r+\pi\Delta r$
$2\pi$
$2\pi$

Volume of a Sphere The volume $V$ of a sphere of radius $r$ is $V=\dfrac{4\pi r^{3}}{3}.$ If the radius changes from $r$ to $r+\Delta r$ , find the:
1. (a) Change in volume
2. (b) Average rate of change of volume with respect to radius
3. (c) Rate of change of volume with respect to radius

Use the definition of the derivative to show that $f( x) =\left\vert x\right\vert$ has no derivative at $0.$

See Student Solutions Manual.

Use the definition of the derivative to show that $f( x) =\sqrt[3]{x}$ has no derivative at $0.$

If $f$ is an even function that is differentiable at $c$ , show that its derivative function is odd. That is, show $f\prime (-c)=-f\prime (c)$ .

See Student Solutions Manual.

If $f$ is an odd function that is differentiable at $c$ , show that its derivative function is even. That is, show $f\prime (-c)=f\prime (c).$

Tangent Lines and Derivatives Let $f$ and $g$ be two functions, each with derivatives at $c$ . State the relationship between their tangent lines at $c$ if:
1. $f\prime (c)=g\prime (c)$
2. ${f}\prime (c)=-{\dfrac{1}{g\prime (c)}}$
3. $g\prime(c)\neq 0$

(a) Parallel
(b) Perpendicular

Challenge Problems

Let $f$ be a function defined for all $x.$ Suppose $f$ has the following properties: $f(u+v)=f(u)f(v) \qquad f(0)=1 \qquad f\prime (0) \hbox{ exists}$
1. Show that $f\prime (x)$ exists for all real numbers $x.$
2. Show that $f\prime (x)=f\prime (0)f(x)$ .

A function $f$ is defined for all real numbers and has the following three properties: $f(1)=5\qquad f(3)=21 \qquad f(a+b)-f(a)=kab+2b^{2}$ for all real numbers $a$ and $b$ where $k$ is a fixed real number independent of $a$ and $b$ .
1. Use $a=1$ and $b=2$ to find $k$ .
2. Find $f\prime (3)$ .
3. Find $f\prime (x)$ for all real $x$ .

$k=4$
$f'(3)=12$
$f'(x)=4x$

A function $f$ is periodic if there is a positive number $p$ so that $f(x+p)=f(x)$ for all $x$ . Suppose $f$ is differentiable. Show that if $f$ is periodic with period $p$ , then $f\prime$ is also periodic with period $p$ .

2.2 Assess Your UnderstandingPrinted Page 160

2.2 Assess Your Understanding
Printed Page 160