2.2 The Derivative as a FunctionPrinted Page 154
154
OBJECTIVES
When you finish this section, you should be able to:
1 Define the Derivative FunctionPrinted Page 154
The derivative of f at a real number c has been defined as the real number \bbox[5px, border:1px solid black, #F9F7ED]{f^\prime (c) =\lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c} }\tag{1}
provided the limit exists. Next we show how to find the derivative of f at any real number. We begin by rewriting the expression \dfrac{f( x) -f( c) }{x-c}. Let x=c+h, h\neq 0.
Then \dfrac{f( x) -f( c) }{x-c}=\dfrac{f\left( c+h\right) -f( c) }{\left( c+h\right) -c}=\dfrac{f\left( c+h\right) -f( c) }{h}
Since x=c+h, as x approaches c, then h approaches 0. Equation (1) with these changes becomes {f^\prime ( c) =\lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c}=\lim\limits_{h\rightarrow 0}\dfrac{f\left( c+h\right) -f( c) }{h}}
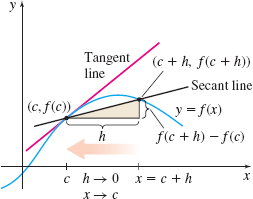
So, we have the following alternate form for the derivative of f at a real number c. \bbox[5px, border:1px solid black, #F9F7ED]{ f^\prime ( c) =\lim\limits_{h\rightarrow 0}\dfrac{f( c+h) -f( c) }{h}}\tag{2}
See Figure 7.
EXAMPLE 1Finding the Derivative of a Function at a Number c
Find the derivative of the function f( x) =x^{2}-5x at any real number c using form (2).
Solution Using form (2), we have \begin{eqnarray*} f^\prime ( c) &=&\lim\limits_{h\rightarrow 0}\dfrac{f(c+h) -f( c) }{h} = \lim\limits_{h\rightarrow 0}\dfrac{[ ( c+h) ^{2}-5( c+h) ] -( c^{2}-5c) }{h} \\[4pt] \notag &=&\lim\limits_{h\rightarrow 0}\dfrac{[ ( c^{2}+2ch+h^{2}) -5c-5h] -c^{2}+5c}{h}=\lim\limits_{h\rightarrow 0}\dfrac{2ch+h^{2}-5h}{ h} \\[4pt] \notag &=&\lim\limits_{h\rightarrow 0}\dfrac{h( 2c+h-5) }{h} =\lim\limits_{h\rightarrow 0}( 2c+h-5) =2c-5 \end{eqnarray*}
NOW WORK
Based on Example 1, if f( x) =x^{2}-5x, then f^\prime ( c) =2c-5 for any choice of c. That is, the derivative f^\prime is a function and, using x as the independent variable, we can write f^\prime ( x) =2x-5.
IN WORDS
In form (3) the derivative is the limit of a difference quotient.
DEFINITION The Derivative Function f^\prime
The derivative function f^\prime of a function f is \bbox[5px, border:1px solid black, #F9F7ED]{ f^\prime ( x) =\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}}\tag{3}
provided the limit exists. If f has a derivative, then f is said to be differentiable.
155
The domain of the function f^\prime is the set of real numbers in the domain of f for which the limit (3) exists. So the domain of f^\prime is a subset of the domain of f.
We can use either form (1) or form (3) to find derivatives. However, if we want the derivative of f at a number c, we usually use form (1) to find f^\prime(c). If we want to find the derivative function of f, we usually use form (3) to find f^\prime(x). In this section, we use the definitions of the derivative, forms (1) and (3), to investigate derivatives. In the next section, we begin to develop formulas for finding the derivatives.
EXAMPLE 2Finding the Derivative Function
Differentiate f(x)=\sqrt{x} and determine the domain of f^\prime.
NOTE
The instruction “differentiate f” means to “find the derivative of f.”
Solution The domain of f is \{x|x ≥ 0\}. To find the derivative of f, we use form (3). Then f^\prime ( x) =\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{\sqrt{ x+h}-\sqrt{x}}{h}
We rationalize the numerator to find the limit. \begin{eqnarray*} f^\prime ( x) &=&\lim\limits_{h\rightarrow 0}\left[ \dfrac{\sqrt{ x+h}-\sqrt{x}}{h}\cdot \dfrac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x} } \right] =\lim\limits_{h\rightarrow 0}\dfrac{( x+h) -x}{ h( \sqrt{x+h}+\sqrt{x}) } \\[5pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{h}{h( \sqrt{x+h}+\sqrt{x}) } =\lim\limits_{h\rightarrow 0}\dfrac{1}{\sqrt{x+h}+\sqrt{x}}=\dfrac{1}{2\sqrt{ x}} \end{eqnarray*}
The limit does not exist when x=0. But for all other x in the domain of f, the limit does exist. So, the domain of the derivative function f^\prime (x) =\dfrac{1}{2\sqrt{x}} is \{ x|x>0\}.
In Example 2, notice that the domain of the derivative function f^\prime is a proper subset of the domain of the function f. The graphs of both f and f^\prime are shown in Figure 8.
NOW WORK
EXAMPLE 3Interpreting the Derivative as a Rate of Change
Show that the rate of change of the area of a circle with respect to its radius is equal to its circumference.
Solution The area A = A(r) of a circle of radius r is A(r) =\pi r^{2}. The derivative function gives the rate of change of the area with respect to the radius. \begin{eqnarray*} A' ( r) &=&\lim\limits_{h\rightarrow 0}\dfrac{A( r+h) -A( r) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{\pi ( r+h) ^{2}-\pi r^{2}}{h}\\[5pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{\pi (r^{2}+2rh+h^{2})-\pi r^{2}}{h}=\lim\limits_{h\rightarrow 0}\dfrac{\pi h( 2r+h) }{h}\\[5pt] &=&\lim\limits_{h\rightarrow 0}\pi ( 2r+h) =2\pi r \end{eqnarray*}
The rate of change of the area of a circle with respect to its radius is the circumference of the circle, 2\pi r.
NOW WORK
2 Graph the Derivative FunctionPrinted Page 155
There is a relationship between the graph of a function and the graph of its derivative.
156
EXAMPLE 4Graphing a Function and Its Derivative
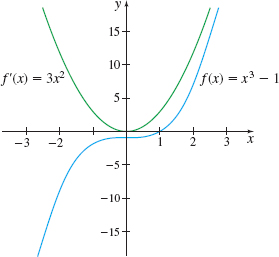
Find f^\prime if f( x) =x^{3}-1. Then graph y=f( x) and y=f^\prime ( x) on the same set of coordinate axes.
Solution f( x) =x^{3}-1 so f( x+h) =( x+h) ^{3}-1=x^{3}+3hx^{2}+3h^{2}x+h^{3}-1 Using form (3), we find \begin{eqnarray*} f^\prime ( x) &=&\lim\limits_{h\rightarrow 0}\dfrac{f( x+h) -f( x) }{h}=\lim\limits_{h\rightarrow 0}\dfrac{( x^{3}+3hx^{2}+3h^{2}x+h^{3}-1) -( x^{3}-1) }{h}\\[7pt] &=&\lim\limits_{h\rightarrow 0}\dfrac{3hx^{2}+3h^{2}x+h^{3}}{h} =\lim\limits_{h\rightarrow 0}\dfrac{h( 3x^{2}+3hx+h^{2}) }{h}\\[7pt] &=&\lim\limits_{h\rightarrow 0}( 3x^{2}{+}3hx{+}h^{2}) =3x^{2} \end{eqnarray*}
The graphs of f and f^\prime are shown in Figure 9.
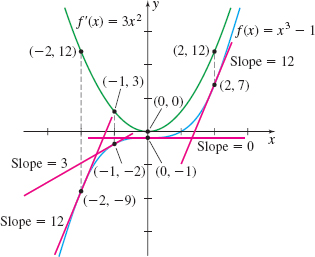
Figure 10 illustrates several tangent lines to the graph of f( x) =x^{3}-1. Observe that the tangent line to the graph of f at ( 0,-1) is horizontal, so its slope is 0. Then f^\prime ( 0) =0, so the graph of f^\prime contains the point ( 0,0) . Also notice that every tangent line to the graph of f has a nonnegative slope, so f^\prime (x) \ge 0. That is, the range of the function f^\prime is \{ y|y ≥ 0\}. Finally, notice that the slope of each tangent line is the y-coordinate of the corresponding point on the graph of the derivative f^\prime.
NOW WORK
With these ideas in mind, we can obtain a rough sketch of the derivative function f^\prime , even if we only know the graph of the function f.
EXAMPLE 5Graphing the Derivative Function
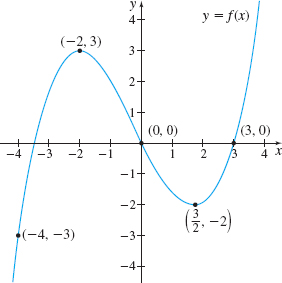
Use the graph of the function y= f(x), shown in Figure 11, to sketch the graph of the derivative function y=f^\prime (x).
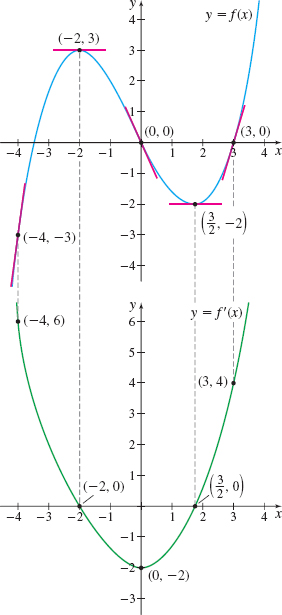
Solution We begin by drawing tangent lines to the graph of f at the points shown in Figure 11. See the graph at the top of Figure 12. At the points (-2, 3) and \left(\dfrac{3}{2},-2\right) the tangent lines are horizontal, so their slopes are 0. This means f^\prime ( -2) =0 and f^\prime \left(\dfrac{3}{2}\right) =0, so the points (-2, 0) and \left(\dfrac{3}{2},0\right) are on the graph of the derivative function. Now we estimate the slope of the tangent lines at the other selected points. For example, at the point ( -4,-3) . the slope of the tangent line is positive and the line is rather steep. We estimate the slope to be close to 6, and we plot the point (-4,6) on the bottom graph of Figure 12. Continue the process and then connect the points with a smooth curve.
Notice in Figure 12 that at the points on the graph of f where the tangent lines are horizontal, the graph of the derivative f^\prime intersects the x-axis. Also notice that wherever the graph of f is increasing, the slopes of the tangent lines are positive, that is, f^\prime is positive, so the graph of f^\prime is above the x-axis. Similarly, wherever the graph of f is decreasing, the slopes of the tangent lines are negative, so the graph of f^\prime is below the x-axis.
157
NOW WORK
3 Identify Where a Function Has No DerivativePrinted Page 157
A function f has no derivative at a number c if \lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c} does not exist. Two (of several) ways this can happen are:
- \lim\limits_{^{{}}x\rightarrow c^{-}}\dfrac{f( x) -f( c) }{x-c} exists and \lim\limits_{^{{}}x\rightarrow c^{+}}\dfrac{ f( x) -f( c) }{x-c} exists, but they are not equal. One way this happens is if the graph of f has a corner at ( c,f( c)). For example, the absolute value function f( x) =\vert x\vert has a corner at ( 0,0) and so has no derivative at 0. See Figure 13. You are asked to prove this in Problem 71.
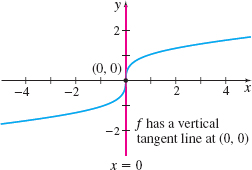
- The limit is infinite. One way this happens is if the graph of f has a vertical tangent line at (c,f( c)). For example, the cube root function f( x) =\sqrt[3]{x} has a vertical tangent line at (0,0) , and so it has no derivative at 0. See Figure 14. You are asked to prove this in Problem 72.
EXAMPLE 6Identifying Where a Function Has No Derivative
Given the piecewise defined function f(x)=\left\{ \begin{array}{r@{\quad}rr} -2x^{2}+4 & \hbox{if} & x<1 \\ x^{2}+1 & \hbox{if} & x ≥ 1 \end{array} \right. , determine if f^\prime (1) exists.
Solution We investigate the limit \lim\limits_{x\rightarrow 1}\frac{f(x)-f(1)}{x-1}=\lim\limits_{x\rightarrow 1}\frac{f(x)-2}{x-1} \qquad {\color{#0066A7}{\hbox{\(f(1)=1^2+1=2\)}}}
If x < 1, then f(x)=-2x^{2}+4; if x ≥ 1, then f(x)=x^{2}+1. So, it is necessary to investigate the one-sided limits at 1. \begin{eqnarray*} \lim\limits_{x\rightarrow 1^{-}}\frac{f(x)-f(1)}{x-1}&=&\lim\limits_{x \rightarrow 1^{-}}\frac{(-2x^{2}+4)-2}{x-1} = \lim\limits_{x\rightarrow 1^{-}} \frac{-2(x^{2}-1)}{x-1}\\[5pt] &=&-2\lim\limits_{x\rightarrow 1^{-}}\frac{(x-1)(x+1)}{ x-1}=-2\lim\limits_{x\rightarrow 1^{-}}(x+1)=-4\\[5pt] \lim\limits_{x\rightarrow 1^{+}}\frac{f(x)-f(1)}{x-1}&=&\lim\limits_{x \rightarrow 1^{+}}\frac{(x^{2}+1)-2}{x-1} = \lim\limits_{x\rightarrow 1^{+}} \frac{(x-1)(x+1)}{x-1} = \lim\limits_{x\rightarrow 1^{+}}(x+1)=2 \end{eqnarray*} Since the one-sided limits are not equal, \lim\limits_{x\rightarrow 1} \dfrac{f( x) -f(1) }{x-1} does not exist, and so f^\prime (1) does not exist.

Figure 15 illustrates the graph of the function f from Example 6. At 1, where the derivative does not exist (and so there is no tangent line), the graph of f has a corner. We usually say that the graph of f is not smooth at a corner.
158
NOW WORK
Example 7 illustrates the behavior of the graph of a function f when the derivative at a number c does not exist because \lim\limits_{x\rightarrow c}\dfrac{f( x) -f( c) }{x-c} is infinite.
EXAMPLE 7Showing That a Function Has No Derivative
Show that f( x) =\sqrt[5]{x+2} has no derivative at x=-2.
Solution First we note that f(-2) =\sqrt[5]{-2+2}=0. Then we investigate the limit. \lim\limits_{x\rightarrow -2}\dfrac{f( x) -f(-2) }{ x-(-2) }=\lim\limits_{x\rightarrow -2}\dfrac{\sqrt[5]{x+2}-0}{x+2 }=\lim\limits_{x\rightarrow -2}\dfrac{\sqrt[5]{x+2}}{x+2}=\lim\limits_{x \rightarrow -2}\dfrac{1}{\sqrt[5]{( x+2) ^{4}}}=\infty
Since the limit is infinite, the derivative of f does not exist at -2.
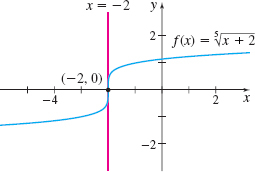
Figure 16 shows that the tangent line to the graph of f at the point (-2,0) is vertical.
NOW WORK
In Chapter 1, we investigated the continuity of a function. Here, we have been investigating the differentiability of a function. An important connection exists between continuity and differentiability.
THEOREM
If a function f has a derivative at a number c, then f is continuous at c.
NEED TO REVIEW?
Continuity is discussed in Section 1.3, pp. 93-99.
PROOF
To show that f is continuous at c, we need to verify that \lim\limits_{x\rightarrow c}f(x)=f(c). We begin by observing that if x\neq c, then f(x)-f(c)=\left[ \frac{f(x)-f(c)}{x-c}\right] (x-c)
We take the limit of both sides as x\rightarrow c, and use the fact that the limit of a product equals the product of the limits, (we show later that each limit exists). \begin{eqnarray*} \lim\limits_{x\rightarrow c}[f(x)-f(c)]&=&\lim\limits_{x\rightarrow c}\left\{ \left[ \frac{f(x)-f(c)}{x-c}\right] (x-c)\right\}\\[6pt] &=&\left[ \lim\limits_{x \rightarrow c}\frac{f(x)-f(c)}{x-c}\right] \left[ \lim\limits_{x\rightarrow c}(x-c)\right] \end{eqnarray*}
Since f has a derivative at c, we know that \lim\limits_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}=f^\prime (c) is a number. Also for any real number c, \lim\limits_{x\rightarrow c}(x-c)=0. So \lim\limits_{x\rightarrow c}[f(x)-f(c)]=[f^\prime (c)]\left[ \lim\limits_{x\rightarrow c}(x-c)\right] =f^\prime (c)\cdot 0=0
That is, \lim\limits_{x\rightarrow c}f(x)=f(c), so f is continuous at c.
159
An equivalent statement of this theorem gives a condition under which a function has no derivative.
COROLLARY
If a function f is discontinuous at a number c, then f has no derivative at c.
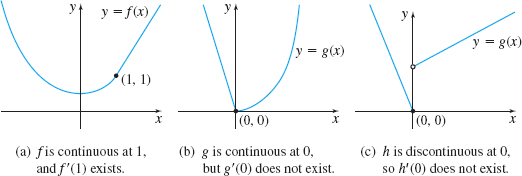
Let’s look at some of the possibilities. In Figure 17(a), the function f is continuous at the number 1 and it has a derivative at 1. The function g, graphed in Figure 17(b), is continuous at the number 0, but it has no derivative at 0. So continuity at a number c provides no prediction about differentiability. On the other hand, the function h graphed in Figure 17(c) illustrates the Corollary: If h is discontinuous at a number, it has no derivative at that number.
IN WORDS
Differentiability implies continuity, but continuity does not imply differentiability.
The corollary is useful if we are seeking the derivative of a function f that we suspect is discontinuous at a number c. If we can show that f is discontinuous at c, then the corollary affirms that the function f has no derivative at c. For example, since the floor function f(x)= \lfloor x\rfloor is discontinuous at every integer c, it has no derivative at an integer.
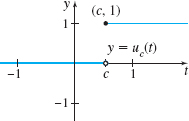
The Heaviside function u_{c}( t) =\left\{ \begin{array}{l@{\quad}l} 0 & \hbox{if} & t < c \\ 1 & \hbox{if} & t ≥ c \end{array} \right. is a step function that is used in electrical engineering to model a switch. The switch is off if t < c and is on if t ≥ c. See Figure 18.
EXAMPLE 8Determining If a Heaviside Function Has a Derivative at 0
Determine if the Heaviside function u_{0}( t) =\left\{ \begin{array}{l@{\quad}ll} 0 & \hbox{if} & t < 0 \\ 1 & \hbox{if} & t ≥ 0 \end{array} \right. has a derivative at 0.
Solution Since u_{0}( t) is discontinuous at 0, it has no derivative at 0.
NOW WORK
Differentiability on a Closed Interval
Special attention needs to be paid to functions defined on a closed interval \left[ a,b\right]. If a function f is defined on a closed interval \left[ a,b \right], we can investigate the derivative of f at every number c in the open interval \left( a,b\right). The endpoints must be handled separately. The right-hand derivative of f at a, for example, is defined as the right-hand limit f^\prime ( a) =\lim\limits_{x\rightarrow a^{+}}\dfrac{f( x) -f( a) }{x-a} provided this limit exists. The left-hand derivative at b is handled similarly as the left-hand limit f^\prime ( b) =\lim\limits_{x\rightarrow b^{-}}\dfrac{f( x) -f( b) }{x-b} provided this limit exists.
160
Using these definitions, we conclude that if f has a derivative at every number c in the closed interval [ a,b], then f is continuous on the closed interval [ a,b].