1. True or False If a function $f$ is defined and continuous on a closed interval $[a,b],$ differentiable on the open interval $(a,b),$ and if $f(a)=f(b)$, then Rolle’s Theorem guarantees that there is at least one number $c$ in the interval $( a,b)$ for which $f( c) =0.$

2. In your own words, give a geometric interpretation of the Mean Value Theorem.

3. True or False If two functions $f$ and $g$ are differentiable on an open interval $( a,b)$ and if $f^\prime (x) =g^\prime (x)$ for all numbers $x$ in $( a,b)$, then $f$ and $g$ differ by a constant on $(a, b)$.

4. True or False When the derivative $f^\prime$ is positive on an open interval $I$, then $f$ is positive on $I$.

5. $f(x)=x^{2}-3x$ on $[0,3]$

6. $f(x)=x^{2}+2x$ on $[-2,0]$

7. $g(x)=x^{2}-2x-2$ on $[0,2]$

8. $g(x)=x^{2}+1$ on $[-1,1]$

9. $f(x)=x^{3}-x$ on $[-1,0]$

10. $f(x)=x^{3}-4x$ on $[-2,2]$

11. $f(t)=t^{3}-t+2$ on $[-1,1]$

12. $f(t)=t^{4}-3$ on $[-2,2]$

13. $s(t)=t^{4}-2t^{2}+1$ on $[-2,2]$

14. $s(t)=t^{4}+t^{2}$ on $[-2,2]$

15. $f(x)=\sin (2x)$ on $[0,\pi ]$

16. $f(x)=\sin x+\cos x$ on $[0,2\pi ]$

17. $f(x)=x^{2}-2x+1$ on $[-2,1]$

18. $f(x)=x^{3}-3x$ on $[2,4]$

19. $f(x)=x^{1/3}-x$ on $[-1,1]$

20. $f(x)=x^{2/5}$ on $[-1,1]$

21. $f(x)=x^{2}+1$ on $[0,2]$

22. $f(x)=x+2+\dfrac{3}{x-1}$ on $[2,7]$

23. $f(x)=\ln \sqrt{x}$ on $[1,e]$

24. $f(x)=xe^{x}$ on $[0,1]$

25. $f(x)=x^{3}-5x^{2}+4x-2$ on $[1,3]$

26. $f(x)=x^{3}-7x^{2}+5x$ on $[-2,2]$

27. $f(x)=\dfrac{x+1}{x}$ on $[1,3]$

28. $f(x)=\dfrac{x^{2}}{x+1}$ on $[0,1]$

29. $f(x)=\sqrt[3]{x^{2}}$ on $[1,8]$

30. $f(x)=\sqrt{x-2}$ on $[2,4]$

31. $f(x)=x^{3}+6x^{2}+12x+1$

32. $f(x)=-x^{3}+3x^{2}+4$

33. $f(x)=x^{2/3}(x^{2}-4)$

34. $f(x)=x^{1/3}(x^{2}-7)$

35. $f(x)=\vert x^{3}+3 \vert$

36. $f(x)=|{x^{2}-4}|$

37. $f(x)=3\sin x$ on $[0,2\pi]$

38. $f(x)=\cos (2x)$ on $[0,2\pi]$

39. $f(x) =xe^{x}$

40. $g(x) =x+e^{x}$

41. $f(x) =e^{x}\sin x$, $0\leq x\leq 2\pi$

42. $f(x) =e^{x}\cos x$, $0\leq x\leq 2\pi$

43. Show that the function $f(x)=2x^{3}-6x^{2}+6x-5$ is increasing for all $x.$

44. Show that the function $f(x)=x^{3}-3x^{2}+3x$ is increasing for all $x.$

45. Show that the function $f(x)=\dfrac{x}{x+1}$ is increasing on any interval not containing $x=-1$.

46. Show that the function $f(x)=\dfrac{x+1}{x}$ is decreasing on any interval not containing $x=0$.

47. Mean Value Theorem Draw the graph of a function $f$ that is continuous on $[a,b]$ but not differentiable on $( a,b) ,$ and for which the conclusion of the Mean Value Theorem does not hold.

48. Mean Value Theorem Draw the graph of a function $f$ that is differentiable on $(a,b)$ but not continuous on $[a,b],$ and for which the conclusion of the Mean Value Theorem does not hold.

49. Rectilinear Motion An automobile travels $20$ mi down a straight road at an average velocity of $40$ mph. Show that the automobile must have a velocity of exactly $40$ mph at some time during the trip. (Assume that the distance function is differentiable.)

283

50. Rectilinear Motion Suppose a car is traveling on a highway. At $4:00\, {\rm p.m.}$, the car’s speedometer reads $40$ mph. At $4:12 \,{\rm p.m.}$, it reads $60$ mph. Show that at some time between $4:00$ and $4:12 {\rm p.m.}$, the acceleration was exactly $100\,{\rm{mi}}/{{\rm{h}}^2}$.

51. Rectilinear Motion Two stock cars start a race at the same time and finish in a tie. If $f_{1}(t)$ is the position of one car at time $t$ and $f_{2}(t)$ is the position of the second car at time $t$, show that at some time during the race they have the same velocity. (Hint: Set $f(t)=f_{2}(t)-f_{1}(t)$.)

52. Rectilinear Motion Suppose $s=f(t)$ is the distance $s$ that an object has traveled from the origin at time $t$. If the object is at a specific location at $t=a,$ and returns to that location at $t=b,$ then $f(a)=f(b)$. Show that there is at least one time $t=c,$ $a<c<b$ for which $f^\prime ( c) =0$. That is, show that there is a time $c$ when the velocity of the object is $0$.

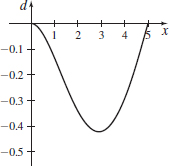
53. Loaded Beam The vertical deflection $d$ (in feet), of a particular $5$-${\rm foot}$-long loaded beam can be approximated by $$d=d(x) =-\dfrac{1}{192}x^{4}+\dfrac{25}{384}x^{3}-\dfrac{25}{128}x^{2}$$

    where $x$ (in feet) is the distance from one end of the beam.

    1. (a) Verify that the function $d=d(x)$ satisfies the conditions of Rolle’s Theorem on the interval $[0,5]$
    2. (b) What does the result in (a) say about the ends of the beam?
    3. (c) Find all numbers $c$ in $(0,5)$ that satisfy the conclusion of Rolle’s Theorem. Then find the deflection $d$ at each number $c.$
    4. (d) Graph the function $d$ on the interval $[0,5]$.

54. For the function $f(x)=x^{4}-2x^{3}-4x^{2}+7x+3$:

    1. (a) Find the critical numbers of $f$ rounded to three decimal places.
    2. (b) Find the intervals where $f$ is increasing and decreasing.

55. Rolle’s Theorem Use Rolle’s Theorem with the function $f(x)=( x-1) \sin x$ on $[0,1]$ to show that the equation $\tan x+x=1$ has a solution in the interval $(0,1)$.

56. Rolle’s Theorem Use Rolle’s Theorem to show that the function $f(x) =x^{3}-2$ has exactly one real zero.

57. Rolle’s Theorem Use Rolle’s Theorem to show that the function $f(x) =(x-8) ^{3}$ has exactly one real zero.

58. Rolle’s Theorem Without finding the derivative, show that if $f(x)=(x^{2}-4x+3)(x^{2}+x+1)$, then $f^\prime (x)=0$ for at least one number between $1$ and $3$. Check by finding the derivative and using the Intermediate Value Theorem.

59. Rolle’s Theorem Consider $f(x)=|x|$ on the interval $[-1,1]$. Here, $f(1)=\,f(-1)=1$ but there is no $c$ in the interval $(-1,1)$ at which $f^\prime (c)=0$. Explain why this does not contradict Rolle’s Theorem.

60. Mean Value Theorem Consider $f(x)=x^{2/3}$ on the interval $[-1,1]$. Verify that there is no $c$ in $({-}1,1)$ for which $$f^\prime (c)=\frac{f(1)-f(-1)}{1-(-1)}$$

    Explain why this does not contradict the Mean Value Theorem.

61. Mean Value Theorem The Mean Value Theorem guarantees that there is a real number $N$ in the interval $(0,1)$ for which $f^\prime (N)=f(1)-f(0)$ if $f$ is continuous on the interval $[0,1]$ and differentiable on the interval $(0,1)$. Find $N$ if $f(x)= \sin ^{-1}x$.

62. Mean Value Theorem Show that when the Mean Value Theorem is applied to the function $f(x)=Ax^{2}+Bx+C$ in the interval $[a,b]$, the number $c$ referred to in the theorem is the midpoint of the interval.

63. 1. (a) Apply the Increasing/Decreasing Function Test to the function $f(x) =\sqrt{x}.$ What do you conclude?
    2. (b) Is $f$ increasing on the interval $[0, \infty)$? Explain.

64. Explain why the function $f(x)=ax^{4}+bx^{3}\,+cx^{2}+dx\,+e\,$ must have a zero between $0$ and $1$ if $$\frac{a}{5}+\frac{b}{4}+\frac{c}{3}+\frac{d}{2}+e=0$$

65. Put It Together If $f^\prime (x)$ and $g^\prime (x)$ exist and $f^\prime (x)>g^\prime (x)$ for all real $x$, then which of the following statements must be true about the graph of $y=f(x)$ and the graph of $y=g(x)$?

    1. (a) They intersect exactly once.
    2. (b) They intersect no more than once.
    3. (c) They do not intersect.
    4. (d) They could intersect more than once.
    5. (e) They have a common tangent at each point of intersection.

66. Prove that there is no $k$ for which the function $$f(x)=x^{3}-3x+k$$

    has two distinct zeros in the interval $[0,1]$.

67. Show that $e^{x}>x^{2}$ for all $x>0$.

68. Show that $e^{x}>1+x$ for all $x>0$. (Hint: Show that $f(x)=e^{x}-1-x$ is an increasing function for $x>0$.)

69. Show that $0<\ln x<x$ for $x>1$.

70. Show that $\tan \theta \geq \theta$ for all $\theta$ in the open interval $\left( 0,\dfrac{\pi }{2}\right).$

71. Let $f$ be a function that is continuous on the closed interval $[a,b]$ and differentiable on the open interval $(a,b)$. If $f(x)=0$ for three different numbers $x$ in $(a,b),$ show that there must be at least two numbers in $(a,b)$ at which $f^\prime (x) =0$.

72. Proof for the Increasing/Decreasing Function Test Let $f$ be a function that is continuous on a closed interval $[ a,b]$. Show that if $f^\prime (x) <0$ for all numbers in $( a,b)$, then $f$ is a decreasing function on $( a,b)$. (See the Corollary on p. 279.)

73. Suppose that the domain of $f$ is an open interval $( a,b)$ and $f^\prime (x)>0$ for all $x$ in the interval. Show that $f$ cannot have an extreme value on $(a,b)$.

74. Use Rolle’s Theorem to show that between any two real zeros of a polynomial function $f$, there is a real zero of its derivative function $f^\prime$.

75. Find where the general cubic $f(x)=ax^{3}+bx^{2}+cx+d$ is increasing and where it is decreasing by considering cases depending on the value of $b^{2}-3ac$. (Hint: $f^\prime (x)$ is a quadratic function; examine its discriminant.)

284

76. Explain why the function $f(x) =$ $x^{n}+ax+b,$ where $n$ is a positive even integer, has at most two distinct real zeros.

77. Explain why the function $f(x) =$ $x^{n} + ax + b,$ where $n$ is a positive odd integer, has at most three distinct real zeros.

78. Explain why the function $f(x) =$ $x^{n} + ax^{2} + b,$ where $n$ is a positive odd integer, has at most three distinct real zeros.

79. Explain why the function $f(x) =$ $x^{n} + ax^{2} + b,$ where $n$ is a positive even integer, has at most four distinct real zeros.

80. Mean Value Theorem Use the Mean Value Theorem to verify that $$\frac{1}{9}<\sqrt{66}-8<\frac{1}{8}$$

    (Hint: Consider $f(x)=\sqrt{x}$ on the interval $[64,66]$.)

81. Given $f(x)=\dfrac{ax^{n}+b}{cx^{n}+d}$, where $n\geq 2$ is a positive integer and $ad-bc\neq 0$, find the critical numbers and the intervals on which $f$ is increasing and decreasing.

82. Show that $x\leq \ln (1+x)^{1+x}$ for all $x>-1$. (Hint: Consider $f(x)=-x+\ln (1+x)^{1+x}$.)

83. Show that $a\ln \dfrac{b}{a}\leq b-a<b\ln \dfrac{b}{a}$ if $0<a<b$.

84. Show that for any positive integer $n,\,\frac{n}{{n + 1}} <\ln {\left( {1 + \frac{1}{n}} \right)^n} < 1.$