Infinite Series

8.9 Assess Your Understanding
Printed Page 622

622

Concepts and Vocabulary

The series representation of a function $f$ given by the power series $f(x) =f(c)+f^{\prime} (c)(x-c)+\frac{f^{\prime \prime} (c) (x-c) ^{2}}{2!}+\cdots+$ $\frac{f^{(n) }(c)\,(x-c)^{n}}{n!}+\cdots$ is called a(n)______________ ______________ about $c$ .

Taylor series

If $c=0$ in the Taylor expansion of a function $f,$ then the expansion is called a(n) ______________ expansion.

Maclaurin

Skill Building

In Problems 3–14, assuming each function can be represented by a power series, find the Maclaurin expansion of each function.

$f(x)=\ln (1-x)$

$f(x) = -\sum\limits_{k=1}^{\infty}{\dfrac{x^{k}}{k}}$

$f(x)=\ln (1+x)$

$f(x)=\frac{1}{1-x}$

$f(x) = \sum\limits_{k=0}^{\infty}{x^{k}}$

$f(x)=\frac{1}{1-3x}$

$f(x)=\frac{1}{(1+x)^{2}}$

$f(x) = \sum\limits_{k=0}^{\infty}{(-1)^{k}(k+1)x^{k}}$

$f(x)=(1+x) ^{-3}$

$f(x)=\frac{1}{1+x^{2}}$

$f(x) = \sum\limits_{k=0}^{\infty}{(-1)^{k}x^{2k}}$

$f(x)=\frac{1}{1+2x^{3}}$

$f(x)=e^{3x}$

$f(x) = \sum\limits_{k=0}^{\infty}{\dfrac{x^{k}3^{k}}{k!}}$

$f(x)=e^{x/2}$

$f(x)=\sin (\pi x)$

$f(x) = \sum\limits_{k=0}^{\infty}{\dfrac{(-1)^{k}\pi^{2k+1}x^{2k+1}}{(2k+1)!}}$

$f(x)=\cos (2x)$

In Problems 15–22, assuming each function can be represented by a power series, find the Taylor expansion of each function about the given number $c.$

$f(x)=e^{x};\quad c=1$

$f(x) = \sum\limits_{k=0}^{\infty}{\dfrac{e(x-1)^{k}}{k!}}$

$f(x)=e^{2x};\quad c=-1$

$f(x)=\ln x;\quad c=1$

$f(x) = \sum\limits_{k=1}^{\infty}{\dfrac{(-1)^{k+1}(x-1)^{k}}{k}}$

$f(x)=\sqrt{x};\quad c=1$

$f(x)=\frac{1}{x};\quad c=1$

$f(x) = \sum\limits_{k=0}^{\infty}{(-1)^{k}(x-1)^{k}}$

$f(x)=\frac{1}{\sqrt{x}};\quad c=4$

$f(x)=\sin x;\quad c=\frac{\pi }{6}$

$f(x) = \sum\limits_{k=0}^{\infty}{\dfrac{\sin{\left(\dfrac{1}{6}(\pi+3k\pi)\right)} \left(x-\dfrac{\pi}{6}\right)^{k}}{k!}}$

$f(x)=\cos x;\quad c=-\frac{\pi }{2}$

In Problems 23–26, assuming each function can be represented by a power series, find the Taylor expansion of each function about the given number $c.$ Comment on the result.

$f(x)=3x^{3}+2x^{2}+5x-6;\quad c=0$

$f (x) = -6 + 5x + 2x^2 + 3x^3$

$f(x)=4x^{4}-2x^{3}-x;\quad c=0$

$f(x)=3x^{3}+2x^{2}+5x-6;\quad c=1$

$f(x) = 4 + 18(x - 1) + 11(x - 1)^2 + 3(x - 1)^3$

$f(x)=4x^{4}-2x^{3}+x;\quad c=1$

In Problems 27 and 28, find the Maclaurin expansion for each function.

$f(x)=\sinh x$

$f(x) = \sum\limits_{k=0}^{\infty}{\dfrac{x^{2k+1}}{(2k+1)!}}$

$f(x)= e^{-x^{2}}$

In Problems 29–32, use properties of power series to find the first five nonzero terms of the Maclaurin expansion.

$f(x)=xe^{x}$

$x+x^{2}+\dfrac{x^{3}}{2}+\dfrac{x^{4}}{6}+\dfrac{x^{5}}{24}$

$f(x)=xe^{-x}$

$f(x)=e^{-x}\sin x$

$x-x^{2}+\dfrac{x^{3}}{3}-\dfrac{x^{5}}{30}+\dfrac{x^{6}}{90}$

$f(x)=e^{-x}\cos x$

In Problems 33 and 34, use a Maclaurin series for $f$ to obtain the first four nonzero terms of the Maclaurin expansion for $g$ .

$f(x)=\frac{1}{\sqrt{1-x^{2}}};\quad g(x)=\sin ^{-1}x$

$x+\dfrac{x^{3}}{6}+\dfrac{3x^{5}}{40}+\dfrac{5x^{7}}{112}$

$f(x)=\tan x;\quad g(x)=\ln (\cos x)$

In Problems 35–42, use a binomial series to represent each function, and find the interval of convergence.

$f(x)= \sqrt{1+x^{2}}$

$\sum\limits_{k=0}^{\infty}{{1/2}\choose {k}}x^{2k}=1+\dfrac{x^{2}}{2}-\dfrac{x^{4}}{8} +\dfrac{x^{6}}{16}+\ldots$ ; interval: $[-1, 1]$

$f(x)=\frac{1}{\sqrt{1-x}}$

$f(x)=(1+x)^{1/5}$

$\sum\limits_{k=0}^{\infty}{{1/5}\choose {k}}x^k=1+\dfrac{x}{5}-\dfrac{2x^{2}}{25} +\dfrac{6x^{3}}{125}+\ldots$ ; interval: $[-1, 1]$

$f(x)=(1-x) ^{5/3}$

$f(x)=\frac{1}{(1+x^{2}) ^{1/2}}$

$\sum\limits_{k=0}^{\infty}{{-1/2}\choose {k}}x^{2k}=1-\dfrac{x^{2}}{2}+\dfrac{3x^{4}}{8} -\dfrac{5x^{6}}{16}+\ldots$ ; interval: $(-1, 1]$

$f(x)=\frac{1}{(1+x)^{3/4}}$

$f(x)= \frac{2x}{\sqrt{1-x}}$

$\sum\limits_{k=1}^{\infty}2{{-1/2}\choose {k}}(-1)^{k}x^{k+1}=2x+x^{2} +\dfrac{3}{4}x^{3}+\dfrac{5}{8}x^{4}+\ldots$ ; interval: $(-1, 1]$

$f(x)=\frac{x}{1+x ^{3}}$

Applications and Extensions

Find the Maclaurin expansion for $f(x) =\sin ^{2}x.$

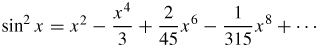
Find the Maclaurin expansion for $f(x) =\cos ^{2}x.$

Obtain the Maclaurin expansion of $\cos x$ by integrating the Maclaurin series for $\sin x$ .

$\cos x = \sum\limits_{k=0}^{\infty}{\dfrac{(-1)^{k}x^{2k}}{(2k)!}}$

Find the Maclaurin expansion for $f(x) =\ln \frac{1}{1-x}$ . Compare the result to the power series representation of $f(x) =\ln \frac{1}{1-x}$ found in Section 8.8, Example 8, page 607.

Find the first five nonzero terms of the Maclaurin expansion for $f(x) =\sec x.$

$\sec{x}= 1+\dfrac{x^{2}}{2}+\dfrac{5x^{4}}{24}+\dfrac{61x^{6}}{720} +\dfrac{277x^{8}}{8064} + \ldots$

Probability The standard normal distribution $p(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2\!/2}$ is important in probability and statistics. If a random variable $Z$ has a standard normal distribution, then the probability that an observation of $Z$ is between $Z=a$ and $Z=b$ is given by $P(a\leq Z\leq b) =\frac{1}{\sqrt{2\pi}}\, \int_{a}^{b} e^{-x^2\!/2}\, dx$
1. Find the Maclaurin expansion for $p(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2\!/2}$ .
2. Use properties of power series to find a power series representation for $P$ .
3. Use the first four terms of the series representation for $P$ to approximate $P(-0.5\leq Z\leq 0.3).$
4. Use technology to approximate $P(-0.5\leq Z\leq 0.3).$

In Problems 49–52, use a Maclaurin expansion to find each integral.

$\int \frac{1}{1+x^{2}}dx$

$C + \sum\limits_{k=0}^{\infty}{\dfrac{(-1)^{k}x^{2k+1}}{2k+1}}$

$\int {\sec x}\,dx$

$\int e^{x^{1/3}}dx$

$C + \sum\limits_{k=0}^{\infty} {\dfrac{3x^{\frac{k}{3}+1}}{(3+k)k!}}$

$\int \ln (1+x)\,dx$

623

Even Functions Show that if $f$ is an even function, then the Maclaurin expansion for $f$ has only even powers of $x.$

See Student Solutions Manual.

Odd Functions Show that if $f$ is an odd function, then the Maclaurin expansion for $f$ has only odd powers of $x.$

Show that $(1+x)^{m}=\sum\limits_{k\,=\,0}^{\infty } {m\choose k}x^{k},$ when $m$ is a nonnegative integer, by showing that $R_{n}(x)\rightarrow 0$ as $n\rightarrow \infty$ .

See Student Solutions Manual.

Show that the series $\sum\limits_{k\,=\,0}^{\infty }{m\choose k}\,x^{k}$ converges absolutely for $\vert x\vert <1$ and diverges for $\vert x\vert >1$ if $m<0$ . (Hint: Use the Ratio Test.)

Show that the interval of convergence of the Maclaurin expansion for $f(x) =\sin ^{-1}x$ is $[-1,1].$

See Student Solutions Manual.

Euler’s Error Euler believed $\frac{1}{2}=1-1+1-1+1-1$ $+\cdots .$ He based his argument to support this equation on his belief in the identification of a series and the values of the function from which it was derived.
1. Write the Maclaurin expansion for $\frac{1}{1+x}$ . Do this without calculating any derivatives.
2. Evaluate both sides of the equation you derived in (a) at $x=1$ to arrive at the formula above.
3. (c) Criticize the procedure used in (b).

Challenge Problems

Find the exact sum of the infinite series: $\frac{x^{3}}{1(3)}-\frac{x^{5}}{3(5)}+\frac{x^{7}}{5(7)} - \frac{x^{9}}{7(9)}+\cdots \quad \hbox{for } x=1$

$\dfrac{\pi}{4} - \dfrac{1}{2}$

Find an elementary expression for $\sum\limits_{k\,=\,1}^{\infty }\frac{x^{k+1}}{k(k+1) }$ . Hint: Integrate the series for $\ln \frac{1}{1-x}$ .

Show that $\sum\limits_{k\,=\,1}^{\infty }\frac{k}{(k+1)!}=1$

See Student Solutions Manual.

Let $s_{n}=\frac{1}{1!}+\frac{1}{2!}+\cdots \,+\frac{1}{n!},\quad n=1, 2, 3, \ldots \,$ .
1. Show that $n!\geq 2^{n-1}$ .
2. Show that $0<s_{n}\leq 1+\frac{1}{2}+\left( \frac{1}{2}\right) ^{2}+\cdots +\left( \frac{1}{2}\right) ^{n-1}$ .
3. Show that $0<s_{n}<s_{n+1}<2$ . Then, conclude that $S=\lim\limits_{n\,\rightarrow \,\infty }s_{n} \,\hbox{and}\, S\leq 2$ .
4. Let $t_{n}=\left[ 1+\frac{1}{n}\right] ^{n}$ . Show that $\begin{eqnarray*} t_{n}&=&1+1+\frac{1}{2!}\left[ 1-\frac{1}{n}\right] + \frac{1}{3!}\left[ 1- \frac{1}{n}\right] \left[ 1-\frac{2}{n}\right] +\cdots \\[4pt] &&+\,\frac{1}{n!} \left[ 1-\frac{1}{n}\right] \left[ 1-\frac{2}{n}\right]\,\cdots \left[ 1-\frac{n-1}{n}\right] <s_{n}+1 \end{eqnarray*}$
5. Show that $0<t_{n}<t_{n+1}<3$ . Then, conclude that $e=\lim\limits_{n\,\rightarrow \,\infty }t_{n}\leq 3$ .

Show that $\left[ 1+\frac{1}{n}\right] ^{n}<e$ for all $n>0$ .

See Student Solutions Manual.

From the fact that $\sin t\leq t$ for all $t\geq 0$ , use integration repeatedly to prove $1-\frac{x^{2}}{2!}\leq \cos x\leq 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}\qquad \hbox{for all }x\geq 0$

Find the first four nonzero terms of the Maclaurin expansion for $f(x) =(1+x) ^{x}.$

$1+x^{2}-\dfrac{x^{3}}{2}+\dfrac{5x^{4}}{6} + \ldots$

Show that $f(x) =\left\{ \begin{array}{l@{\quad}l} e^{-1/x^{2}} & x\neq 0 \\ 0 & x=0 \end{array} \right.$ has a Maclaurin expansion at $x=0.$ Then show that the Maclaurin series does not converge to $f.$

8.9 Assess Your UnderstandingPrinted Page 622

8.9 Assess Your Understanding
Printed Page 622