8.10 Assess Your UnderstandingPrinted Page 628
Skill Building
- (a) Approximate y=cosx by using the first four nonzero terms of its Maclaurin expansion.
- (b) Graph y=cosx along with the approximation found in (a).
- (c) Use the approximation in (a) to approximate cosπ90,(2∘)
- (d) What is the error in using this approximation?
- (e) If the approximation in (a) is used, for what values of x is the error less than 0.0001?
- (a) 1−x22!+x44!−x66!
- (b)
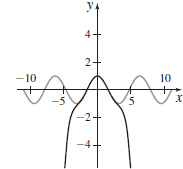
- (c) cos(π/90)≈0.999
- (d) |E|≤5.47×10−17
- (e) |x|≤1.1904
- (a) Approximate y=ex by using the first four nonzero terms of its Maclaurin expansion.
- (b) Graph y=ex along with the approximation found in (a).
- (c) Use the approximation in (a) to approximate e1/2.
- (d) What is the error in using this approximation?
- (e) If the approximation in (a) is used, for what values of x is the error less than 0.0001?
- (a) Represent the function f(x)=3√1+x as a Maclaurin series.
- (b) What is the interval of convergence?
- (c) Approximate y=3√1+x using the first five terms of its Maclaurin series.
- (d)
 Graph y=3√1+x along with the approximation found in (c).
Graph y=3√1+x along with the approximation found in (c). - (e) Comment on the graphs in (d) and the result of the approximation.
- (f) Use the result from (c) to approximate 3√0.9. What is the error in using this approximation?
- (a) \sum\limits_{k=0}^{\infty} {{1/3}\choose {k}}x^k
- (b) [-1,1]
- (c) 1+\dfrac{x}{3}-\dfrac{x^2}{9}+\dfrac{5x^3}{81}-\dfrac{10x^4}{243}
- (d)
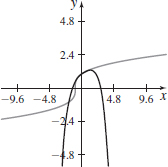
- (e) Answers will vary.
- (f) \approx\! 0.965; the error is \leq 3.018\times 10^{-7}
- (a) Represent y=\dfrac{1}{\sqrt{4+x}} as a Maclaurin series.
- (b) What is the interval of convergence?
- (c) Approximate y=\dfrac{1}{\sqrt{4+x}} using the first four terms of its Maclaurin series.
- (d)
 Graph y=\dfrac{1}{\sqrt{4+x}} along with the approximation found in (c).
Graph y=\dfrac{1}{\sqrt{4+x}} along with the approximation found in (c). - (e) Comment on the graphs in (d) and the result of the approximation.
- (f) Use the result from (c) to approximate \dfrac{1}{\sqrt{4.2}}. What is the error in using this approximation?
- (a) Represent y=\tan ^{-1} x as a Maclaurin series.
- (b) What is the interval of convergence?
- (c) Approximate y=\tan ^{-1} x using the first five nonzero terms of its Maclaurin series.
- (d)
 Graph y=\tan ^{-1} x along with the approximation found in (c).
Graph y=\tan ^{-1} x along with the approximation found in (c). - (e) Comment on the graphs in (d) and the result of the approximation.
- (a) \sum\limits_{k=0}^{\infty} {\dfrac{(-1)^k x^{1+2k}}{1+2k}}
- (b) [-1,1]
- (c) x-\dfrac{x^3}{3}+\dfrac{x^5}{5}-\dfrac{x^7}{7}+\dfrac{x^9}{9}
- (d)
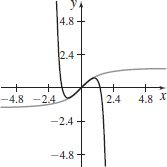
- (e) Answers will vary.
- (a) Represent y=\dfrac{1}{1-x} as a Maclaurin series.
- (b) What is the interval of convergence?
- (c) Approximate y=\dfrac{1}{1-x} using the first four nonzero terms of its Maclaurin series.
- (d)
 Graph y=\dfrac{1}{1-x} along with the approximation found in (c).
Graph y=\dfrac{1}{1-x} along with the approximation found in (c). - (e) Comment on the graphs in (d) and the result of the approximation.
In Problems 7–14, use properties of power series to approximate each integral using the first four terms of a Maclaurin series.
\int_{0}^{1}\sin \, x^{2}dx
0.310
\int_{0}^{1}\cos \,x^{2}\,dx
\int_{0}^{1}\dfrac{x^{2}}{1+\cos x}dx
0.195
\int_{0}^{0.1}\dfrac{x}{\ln \,(2+x)}\,dx
629
\int_{0}^{0.2}\sqrt[3]{1+x^{4}}\,dx
0.200
\int_{0}^{1/2}\sqrt[3]{1+x}\,dx
\int_{0}^{1/2}\dfrac{1}{\sqrt[3]{1+x^{2}}}\,dx
0.487
\int_{0}^{0.2}\dfrac{1}{\sqrt{1+x^{3}}}\,dx
Applications and Extensions
Use the recursive formula (7) for \ln (N+1) to show \ln 4\approx 1.38629.
See Student Solutions Manual.
- (a) Write the first three nonzero terms and the general term of the Maclaurin series for f(x)=3\sin \,\left( \dfrac{x}{2}\right) .
- (b) What is the interval of convergence for the series found in (a)?
- (c) What is the minimum number of terms of the series in (a) that are necessary to approximate f on the interval (-2,~2) with an error less than or equal to 0.1?
Calculators Are Perfect, Right? They always get the right answer with what looks like little or no effort at all. This is very misleading because calculators use a lot of the ideas learned in this chapter to obtain these answers. One advantage we have over a calculator is that we can approximate answers up to any accuracy we choose. So let’s prove you are smarter than any calculator by approximating each of the following correct to within 0.001 using a Maclaurin series.
- (a) F(x) =\sin x, \, x=4{{}^\circ}
- (b) F(x) =\cos x, \, x=15{{}^\circ}
- (c) F(x) =\tan ^{-1}x, \, x=0.05
Source: Contributed by the students at Lander University, Greenwood, SC.
- (a) 0.0698
- (b) 0.9659
- (c) 0.04996
Leibniz Formula for {\pi} Leibniz derived the following formula for \dfrac{\pi }{4}: \dfrac{\pi}{4}=1-\dfrac{1}{3}+\dfrac{1}{5} -\dfrac{1}{7}+\dfrac{1}{9}-\cdots.
- (a) Find \int_{0}^{1}\dfrac{1}{1+x^{2}}\,dx.
- (b) Expand the integrand in (a) into a power series and integrate it term-by-term to get Leibniz’s formula.
- (c) Find the sum of the first 10 terms in the above series. Does it appear that Leibniz’s formula is useful for approximating \pi ?
- (d) How many terms are required to approximate \pi correct to 10 decimal places?
Approximating {\pi} The series approximation of \pi using Gregory’s series converges very slowly. (See Problem 82, Section 8.8. p. 611.) A more rapidly convergent series is obtained by using the identity \tan ^{-1}1=\tan ^{-1} \, \left( \dfrac{1}{2}\right) +\tan ^{-1} \,\left( \dfrac{1}{3}\right)
Use x=\dfrac{1}{2} and x=\dfrac{1}{3} in Gregory’s series, together with this identity, to approximate \pi using the first four terms.
1538665/489888\approx 3.14085
Faster than light? At low speeds, the kinetic energy K, that is, the energy due to the motion of an object of mass m and speed v, is given by the formula K=K(v) =\dfrac{1}{2}mv^{2}. But this formula is only an approximation to the general formula, and works only for speeds much less than the speed of light, c. The general formula, which holds for all speeds, is K_{\text{gen}}(v) =mc^{2} \,\left( \dfrac{1}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}-1\right)
The formula for K was used very successfully for many years before Einstein arrived at the general formula, so K must be essentially correct for low speeds. Use a binomial expansion to show that \dfrac{1}{2}mv^{2} is a first approximation to K_{\text{gen}} for v close to 0.
Challenge Problems
Let a_{k}=(-1)^{k+1}\int_{0}^{\pi /k}\sin (kx)\,dx.
- (a) Find a_{k}.
- (b) Show that the infinite series \sum\limits_{k\,=\,1}^{\infty}a_{k} converges.
- (c) Show that 1\leq \sum\limits_{k=1}^{\infty }a_{k}\leq \dfrac{3}{2}.
- (a) (-1)^{k+1}\dfrac{2}{k}
- (b) See Student Solutions Manual
- (c) See Student Solutions Manual
Find the Maclaurin expansion for f(x) = xe^{x^{3}}.
- (a) Use the Maclaurin expansion for f(x) =\sin ^{-1} \,x to find numerical series for \dfrac{\pi }{2} and for \dfrac{\pi }{6}.
- (b) Use the result of (a) to approximate \dfrac{\pi }{2} correct to within 0.001.
- (c) Use the result of (a) to approximate \dfrac{\pi }{6} correct to within 0.001.
- (a) See Student Solutions Manual.
- (b) 1.571
- (c) 0.524
