Question

Multiple Choice If \(a_{1}\), \(a_{2}\), \(\ldots ,\) \(a_{n},\) \(\ldots\) is an infinite collection of numbers, the expression \(\sum\limits_{k\,=\,1}^{\infty }a_{k}=a_{1}+ a_{2}+ \cdots + a_{n}+ \cdots\) is called [(a) an infinite sequence, (b) an infinite series, (c) a partial sum].

Question

Multiple Choice If \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) is an infinite series, then the sequence \(\{S_{n}\}\) where \(S_{n}=\sum\limits_{k\,=\,1}^{n}a_{k},\) is called the sequence of [(a) fractional parts, (b) early terms, (c) completeness, (d) partial sums] of the infinite series.

Question

True or False A series converges if and only if its sequence of partial sums converges.

Question

True or False A geometric series \(\sum\limits_{k\,=\,1}^{\infty }ar^{k-1},\) \(a\neq 0,\) converges if \(\vert r\vert \leq 1.\)

Question

The sum of a convergent geometric series \(\sum\limits_{k\,=\,1}^{\infty }ar^{k-1},\) \(a\neq 0,\) is \(S= \)______________.

Question

True or False The harmonic series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k}\) converges because \(\lim\limits_{n\,\rightarrow \,\infty }\dfrac{1}{n}=0.\)

Question

\(\sum\limits_{k=1}^{\infty }\left( \dfrac{3}{4}\right) ^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }\dfrac{(-1)^{k+1}}{3^{k-1}}\)

Question

\(\sum\limits_{k=1}^{\infty }k\)

Question

\(\sum\limits_{k=1}^{\infty }\ln k\)

Question

\(\sum\limits_{k=1}^{\infty }\left( \dfrac{1}{k+2}-\dfrac{1}{k+3}\right)\)

Question

\(\sum\limits_{k=1}^{\infty }\left[ \dfrac{1}{k^{2}}-\dfrac{1}{(k+1)^{2}}\right]\)

Question

\(\sum\limits_{k=1}^{\infty }\left( \dfrac{1}{3^{k+1}}-\dfrac{1}{3^{k}}\right)\)

Question

\(\sum\limits_{k=1}^{\infty }\left( \dfrac{1}{4^{k+1}}-\dfrac{1}{4^{k}}\right)\)

Question

\(\sum\limits_{k=1}^{\infty }\dfrac{1}{4k^{2}-1}\) \(\left[Hint: \dfrac{1}{4k^{2}-1}=\dfrac{1}{2}\left( \dfrac{1}{2k-1}-\dfrac{1}{2k+1}\right) \right]\)

Question

\(\sum\limits_{k=1}^{\infty }\dfrac{1}{k(k+1)(k+2)}\) \(\left[Hint: \dfrac{1}{k(k+1)(k+2)} = \dfrac{1}{2}\left( \dfrac{1}{k(k+1)}-\dfrac{1}{(k+1)(k+2)}\right) \right]\)

Question

\(\sum\limits_{k=1}^{\infty }(\sqrt{2})^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }(0.33)^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }5 \left(\dfrac{1}{6}\right)^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }4\left( 1.1\right) ^{k-1} \)

Question

\(\sum\limits_{k\,=\,0}^{\infty }7 \left( \dfrac{1}{3}\right) ^{k}\)

Question

\(\sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{7}{4}\right)^{k}\)

Question

\(\sum\limits_{k=1}^{\infty }( -0.38)^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }(-0.38)^{k}\)

Question

\(\sum\limits_{k\,=\,0}^{\infty }\dfrac{2^{k+1}}{3^{k}}\)

Question

\(\sum\limits_{k\,=\,0}^{\infty }\dfrac{5^{k}}{6^{k+1}}\)

Question

\(\sum\limits_{k\,=\,0}^{\infty }\dfrac{1}{4^{k+1}}\)

Question

\(\sum\limits_{k\,=\,0}^{\infty }\dfrac{4^{k+1}}{3^{k}}\)

Question

\(\sum\limits_{k=1}^{\infty }\sin ^{k-1} \left(\dfrac{\pi }{2}\right)\)

Question

\(\sum\limits_{k=1}^{\infty}\tan ^{k-1} \left( \dfrac{\pi }{4}\right)\)

Question

\(\sum\limits_{k=1}^{\infty }\left( -\dfrac{3}{2}\right)^{k-1}\)

Question

\(\sum\limits_{k=1}^{\infty }\left( -\dfrac{2}{3}\right)^{k-1}\)

Question

\(1+\dfrac{1}{3}+\dfrac{1}{9}+\cdots +\left( \dfrac{1}{3}\right)^{n}+\cdots\)

Question

\(1+\dfrac{1}{4}+\dfrac{1}{16}+\cdots +\left( {\dfrac{1}{4}}\right)^{n}+\cdots\)

Question

\(1+2+4+\cdots +2^{n}+\cdots\)

Question

\(1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\cdots + \dfrac{(-1)^{n-1}}{2^{n-1}}+\cdots\)

Question

\(\left( \dfrac{1}{7}\right) ^{2}+\left( \dfrac{1}{7}\right)^{3}+\cdots +\left( \dfrac{1}{7}\right) ^{n}+\cdots\)

Question

\(\left( \dfrac{3}{4}\right) ^{5}+\left( \dfrac{3}{4}\right)^{6}+\cdots +\left( \dfrac{3}{4}\right) ^{n}+\cdots\)

Question

\(\sum\limits_{k\,=\,0}^{\infty}\dfrac{1}{k+1}\)

Question

\(\sum\limits_{k=4}^{\infty}k^{-1}\)

Question

\(\sum\limits_{k=1}^{\infty}\dfrac{1}{100^{k}}\)

Question

\(\sum\limits_{k=1}^{\infty}e^{-k}\)

Question

\(\sum\limits_{k=1}^{\infty} (-10k)\)

Question

\(\sum\limits_{k=1}^{\infty}\dfrac{3k}{5}\)

Question

\(\sum\limits_{k=1}^{\infty}\cos^{k-1} \left( \dfrac{2\pi }{3}\right)\)

Question

\(\sum\limits_{k=1}^{\infty}\sin^{k-1} \left( \dfrac{\pi }{6}\right)\)

Question

\(\sum\limits_{k=1}^{\infty}\dfrac{\tan ^{k}\left(\dfrac{\pi }{4}\right) }{k}\)

Question

\(\sum\limits_{k=1}^{\infty}\dfrac{\sin ^{k} \left(\dfrac{\pi }{2}\right) }{k}\)

Question

\(\sum\limits_{k=1}^{\infty }\cos (\pi k)\)

Question

\(\sum\limits_{k=1}^{\infty}\sin \left( \dfrac{\pi k}{2}\right)\)

Question

\(\sum\limits_{k=1}^{\infty}2^{-k}3^{k+1}\)

Question

\(\sum\limits_{k=1}^{\infty}3^{1-k}2^{1+k}\)

Question

\(\sum\limits_{k=1}^{\infty}\left( -\dfrac{1}{3}\right)^{k}\)

Question

\(\sum\limits_{k=1}^{\infty}\dfrac{\pi }{3^{k}}\)

Question

\(\sum\limits_{k=1}^{\infty}\ln \dfrac{k}{k+1}\)

Question

\(\sum\limits_{k=1}^{\infty}\left[e^{2k^{-1}}-e^{2(k+1) ^{-1}}\right]\)

Question

\(\sum\limits_{k=1}^{\infty }\left(\sin \dfrac{1}{k}-\sin \dfrac{1}{k+1}\right)\)

Question

\(\sum\limits_{k=1}^{\infty }\left( \tan \dfrac{1}{k}-\tan \dfrac{1}{k+1}\right)\)

Question

\(0.5555\ldots\)

Question

\(0.727272\ldots\)

Question

\(4.28555\ldots \) \((Hint: 4.28555\ldots =4.28+0.00555\ldots .)\)

Question

\(7.162162\ldots\)

Question

Distance a Ball Travels A ball is dropped from a height of 18 ft. Each time it strikes the ground, it bounces back to two-thirds of the previous height. Find the total distance traveled by the ball.

Question

Diminishing Returns A rich man promises to give you \($ 1000\) on January 1, 2015. Each day thereafter he will give you \(\dfrac{9}{10} \) of what he gave you the previous day.

1. What is the total amount you will receive?
2. What is the first date on which the amount you receive is less than \(1\) cent?

Question

Stocking a Lake Mirror Lake is stocked periodically with rainbow trout. In year \(n\) of the stocking program, the population is given by \(p_{n}=3000r^{n}+h\sum\limits_{k=1}^{n}r^{k-1},\) where \(h\) is the number of fish added by the program per year and \(r, 0 < r < 1\), is the percent of fish removed each year.

1. What does a manager expect the steady rainbow trout population to be as \(n\rightarrow \infty ?\)
2. If \(r=0.5,\) how many fish \(h\) should be added annually to obtain a steady population of \(4000\) rainbow trout?

Question

Marginal Propensity to Consume Suppose that individuals in the United States spend 90% of every additional dollar that they earn. Then according to economists, an individual’s marginal propensity to consume is 0.90. For example, if Jane earns an additional dollar, she will spend \(0.9(1)\) =\($0.90\) of it. The individual who earns Jane’s \($0.90\) will spend 90% of it or \(\$0.81.\)

The process of spending continues and results in the series \[ \sum\limits_{k=1}^{\infty }0.90^{k-1}=1+0.90+0.90^{2}+0.90^{3}+\ldots \]

The sum of this series is called the multiplier. What is the multiplier if the marginal propensity to consume is 90%?

Question

Stock Pricing One method of pricing a stock is to discount the stream of future dividends of the stock. Suppose a stock currently pays \($P\) annually in dividends, and historically, the dividend has increased by \(i\%\) annually. If an investor wants an annual rate of return of \(r\%,\) this method of pricing a stock states that the stock should be priced at the present value of an infinite stream of payments: \[ \text{Price}= {\it P}+ {\it P} \dfrac{1+i}{1+r}+ {\it P}\left( \dfrac{1+i}{1+r}\right) ^{2}+ {\it P}\left( \dfrac{1+i}{1+r}\right) ^{3}+\ldots \]

1. Find the price of a stock priced using this method.
2. Suppose an investor desires a \(9\%\) return on a stock that currently pays an annual dividend of \(\$4.00,\) and, historically, the dividend has been increased by \(3\%\) annually. What is the highest price the investor should pay for the stock?

Question

Koch’s Snowflake The area inside the fractal known as the Koch snowflake can be described as the sum of the areas of infinitely many equilateral triangles. See the figure. For all but the center (largest) triangle, a triangle in the Koch snowflake is \(\dfrac{1}{9}\) the area of the next largest triangle in the fractal. Suppose the largest(center) triangle has an area of 1 square unit. Then the area of the snowflake is given by the series \[ 1+3 \left( \dfrac{1}{9}\right) +12 \left( \dfrac{1}{9}\right) ^{2}+48 \left( \dfrac{1}{9}\right) ^{3}+192 \left( \dfrac{1}{9}\right) ^{4}+\ldots \]

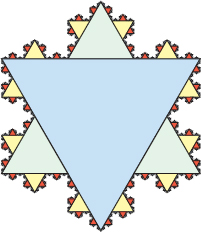
Find the area of the Koch snowflake by finding the sum of the series.

Question

Zeno’s paradox is about a race between Achilles and a tortoise. The tortoise is allowed a certain lead at the start of the race. Zeno claimed the tortoise must win such a race. He reasoned that for Achilles to overtake the tortoise, at some time he must cover \(\dfrac{1}{2}\) of the distance that originally separated them. Then, when he covers another \(\dfrac{1}{4}\) of the original distance separating them, he will still have \(\dfrac{1}{4}\) of that distance remaining, and so on. Therefore by Zeno’s reasoning, Achilles never catches the tortoise. Use a series argument to explain this paradox. Assume that the difference in speed between Achilles and the tortoise is a constant \(v\) meters per second.

Question

Probability A coin-flipping game involves two people who successively flip a coin. The first person to obtain a head is the winner. In probability, it turns out that the person who flips first has the probability of winning given by the series below. Find this probability. \[ \frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\cdots +\frac{1}{2^{2n-1}}+\cdots \]

Question

Controlling Salmonella Salmonella is a common enteric bacterium infecting both humans and farm animals with salmonellosis. Barn surfaces contaminated with salmonella can be the major source of salmonellosis spread in a farm. While cleaning barn surfaces is used as a control measure on pig and cattle farms, the efficiency of cleaning has been a concern. Suppose, on average, there are \(p\) kilograms (kg) of feces produced each day and cleaning is performed with the constant efficiency \(e,\) \(0<e<1.\) At the end of each day, \((1-e)\) kg of feces from the previous day is added to the amount of the present day. Let \(T(n)\) be the total accumulated fecal material on day \(n.\) Farmers are concerned when \(T(n)\) exceeds the threshold level \(L.\)

1. Express \(T(n)\) as a geometric series.
2. Find \(\lim\limits_{n\rightarrow \infty }T(n)\).
3. Determine the minimum cleaning efficiency \(e_{\min }\) required to guarantee \(T(n) \leq L\) for all \(n.\)
4. Suppose that \(p=120 kg\) and \(L=180 kg.\) Using (b) and (c), find \(e_{\min }\) and \(T(365)\) for \(e=\dfrac{4}{5}.\)

   Source: R. Gautam, G. Lahodny, M. Bani-Yaghoub, R. Ivanek Based on their paper “Understanding the role of cleaning in the control of Salmonella Typhimurium in a grower finisher pig herd: a modeling approach.”

Question

Show that \(0.9999 \ldots\,=1.\)

Question

\(\dfrac{x}{x-1}=\sum\limits_{k=1}^{\infty }\dfrac{1}{x^{k-1}}\) for \(\vert x\vert >1\)

Question

\(\dfrac{1}{1+x}=\sum\limits_{k\,=\,0}^{\infty }(-1)^{k}x^{k}\) for \(\vert x\vert <1\)

Question

Find the smallest number \(n\) for which \(\sum\limits_{k=1}^{n}\dfrac{1}{k}\geq 3\).

Question

Find the smallest number \(n\) for which \(\sum\limits_{k=1}^{n}\dfrac{1}{k}\geq 4\).

Question

Show that the series \(\sum\limits_{k=1}^{\infty }\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k(k+1)}}\) converges and has the sum \(1\).

Question

Show that \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k(k+2)}=\dfrac{3}{4}\).

Question

Show that \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k(k+1)(k+2)}=\dfrac{1}{4}\).

Question

Show that \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k(k+1)(k+2)(k+3)}=\dfrac{1}{18}\).

Question

Show that \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k(k+1)(k+2)\cdots (k+a)}=\dfrac{1}{a}\left( \dfrac{1}{a!}\right)\); \(a\geq 1\) is an integer.

Question

Solve for \(x\): \(\dfrac{x}{2+2x}=x+x^{2}+x^{3}+\cdots, |x| < 1\).

Question

Show that the sum of any convergent geometric series whose first term and common ratio are rational is rational.

Question

The sum \(S_{n}\) of the first \(n\) terms of a geometric series is given by the formula \[ S_{n}=a + ar + ar^{2} + \cdots + ar^{n-1}=\frac{a(r^{n}-1)}{r-1}\qquad a>0,\quad r\neq 1 \]

Find \(\lim\limits_{r\rightarrow 1}\dfrac{a(r^{n}-1)}{r-1}\) and compare the result with a geometric series in which \(r=1\).

Question

The harmonic series diverges quite slowly. For example, the partial sums \(S_{10}, S_{20}, S_{50}\), and \(S_{100}\) have approximate values \(2.92897\), \(3.59774\), \(4.49921\), and \(5.18738\), respectively. In fact, the sum of the first million terms of the harmonic series is about \(14.4\). With this in mind, what would you conjecture about the rate of convergence of the limit defining \(\gamma \)? Test your conjecture by calculating approximate values for \(\gamma\) by using the partial sums given above.

Question

Use the approximate value of Euler’s number \(0.5772\) to approximate \[ 1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{1{,}000{,}000{,}000} \]

Question

Show that a real number has a repeating decimal if and only if it is rational.

Question

1. Suppose \(\sum\limits_{k\,=\,1}^{\infty }s_{k}\) is a series with the property that \(s_{n}\geq 0\) for all integers \(n\geq 1.\) Show that \( \sum\limits_{k\,=\,1}^{\infty }s_{k}\) converges if and only if the sequence \( \{S_{n}\} \) of partial sums is bounded.
2. Use the result of (a) to show the harmonic series diverges.