OBJECTIVES

When you finish this section, you should be able to:

1. Use the Test for Divergence (p. 567)
2. Work with properties of series (p. 567)
3. Use the Integral Test (p. 569)
4. Analyze a \(p\)-series (p. 570)

IN WORDS

If \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) converges, then \(\lim\limits_{n\rightarrow \infty}{ a}_{n}\) equals \(0.\) If \(\lim\limits_{n\,\rightarrow\,\infty }{a}_{n}\) equals \(0\), then the series \(\sum\limits_{k\,=\,1}^{\infty }{ a}_{k}\) may converge or diverge.

THEOREM

If the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) converges, then \(\lim\limits_{n\,\rightarrow \,\infty }a_{n}=0\).

Proof

The \(n{\text{th }}\) partial sum of \(\sum\limits_{k\,= \,1}^{\infty }a_{k}\) is \(S_{n}=\sum\limits_{k\,=\,1}^{n}a_{k}\). Since \( S_{n-1}=\sum\limits_{k\,=\,1}^{n-1}a_{k}\), it follows that \[ a_{n}=S_{n}-S_{n-1} \]

Since the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) converges, the sequence \(\{S_{n}\}\) of partial sums has a limit \(S\). Then \(\lim\limits_{n\, \rightarrow \,\infty }S_{n}=S\) and \(\lim\limits_{n\,\rightarrow \,\infty }S_{n-1}=S\), so \[ \lim_{n\,\rightarrow \infty }a_{n}=\lim_{n\,\rightarrow \infty }(S_{n}-S_{n-1})=\lim\limits_{n\rightarrow \infty }S_{n}-\lim_{n\rightarrow \infty }S_{n-1}=S-S=0 \]

THEOREM Test for Divergence

The infinite series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) diverges if \(\lim\limits_{n\,\rightarrow \,\infty }\,a_{n}\neq 0.\)

Using the Test for Divergence

1. \(\sum\limits_{k\,=\,1}^{\infty }87\) diverges, since \(\lim\limits_{n\,\rightarrow \,\infty }87=87\neq 0\).
2. \(\sum\limits_{k\,=\,1}^{\infty }k\) diverges, since \( \lim\limits_{n\,\rightarrow \,\infty }n=\infty \neq 0\).
3. \(\sum\limits_{k\,=\,1}^{\infty }(-1)^{k}\) diverges, since \( \lim\limits_{n\,\rightarrow \,\infty }\,(-1)^{n}\) does not exist.
4. \(\sum\limits_{k\,=\,1}^{\infty }2^{k}\) diverges, since \( \lim\limits_{n\,\rightarrow \,\infty }\,2^{n}=\infty \neq 0\).

NOW WORK

Problem 17.

THEOREM

If two infinite series are identical after a certain term, then either both series converge or both series diverge. If both series converge, they do not necessarily have the same sum.

Proof

Consider the two series \[ \begin{eqnarray*} \sum_{k\,=\,1}^{\infty }a_{k} &=& a_{1}+a_{2}+\cdots +a_{p}+a_{p+1}+\cdots +a_{n}+\cdots \\[5pt] \sum_{k\,=\,1}^{\infty }b_{k} &=& b_{1}+b_{2}+\cdots +b_{p}+a_{p+1}+\cdots +a_{n}+\cdots \end{eqnarray*} \]

Notice that after the first \(p\) terms, the remaining terms of both series are identical. The sequence \(\{S_{n}\}\) of partial sums of \( \sum\limits_{k\,=\,1}^{\infty }a_{k}\) and the sequence \(\{T_{n}\}\) of partial sums of \(\sum\limits_{k\,=\,1}^{\infty }b_{k}\) are given by \[ \begin{eqnarray*} S_{n}& =a_{1}+a_{2}+\cdots +a_{p}+a_{p+1}+\cdots +a_{n} \\[5pt] T_{n}& =b_{1}+b_{2}+\cdots +b_{p}+a_{p+1}+\cdots +a_{n} \end{eqnarray*} \]

Now, \[ \begin{eqnarray*} \begin{array}{@{}rl@{}l} S_{n}-T_{n} &= \left({a_{1}+\cdots +a_{p}}\right) -(b_{1}+\cdots +b_{p}) & {\color{#00ADEE}{{\hbox{ After the }}}{\color{#00ADEE}{p\hbox{th}}} {\color{#00ADEE}{\hbox{ term, the}}}} \\[-1.5pt] && {\color{#00ADEE}{{\hbox{ terms are the same.}}}}\\[4.5pt] S_{n} &= T_{n}+\left({a_{1}+\cdots +a_{p}}\right) -(b_{1}+\cdots +b_{p}) & {\color{#00ADEE}{{\hbox{ For } n>p.}}} \\[7pt] \lim\limits_{n\,\rightarrow \,\infty }S_{n}&= \lim\limits_{n\,\rightarrow \,\infty } \, \, \left[  T_{n}+(a_{1}+\cdots +a_{p})-(b_{1}+\cdots +b_{p})\right]\\[11pt] \lim\limits_{n\,\rightarrow \,\infty }S_{n} &= \lim\limits_{n\,\rightarrow \,\infty }T_{n}+\lim\limits_{n\,\rightarrow \,\infty }\,\,\left[ (a_{1}+\cdots + a_{p})-(b_{1}+\cdots +b_{p})\right] \\[11pt] \lim\limits_{n\,\rightarrow \,\infty }S_{n} &= \lim\limits_{n\,\rightarrow \,\infty }T_{n}+k & {\color{#00ADEE}{{\hbox{\(k=(a_1+ \cdots +a_p)\)}}}}\\[-5pt] &&{\color{#00ADEE}{{\hbox{\(-(b_1 + \cdots +b_p)\)}}}}\\[-1.5pt] &&{\color{#00ADEE}{{\hbox{is some number.}}}} \end{array} \end{eqnarray*} \]

Consequently, either both limits exist (both series converge) or neither limit exists (both series diverge). No other possibility can occur.

THEOREM Sum and Difference of Convergent Series

If \(\sum\limits_{k\,=\,1}^{\infty }a_{k}=S\) and \( \sum\limits_{k\,=\,1}^{\infty }b_{k}=T\) are two convergent series, then the series \(\sum\limits_{k\,=\,1}^{\infty }\,(a_{k}+\,b_{k})\) and the series \(\sum\limits_{k\,=\,1}^{\infty }(a_{k}-\,b_{k})\) also converge. Moreover, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,1}^{\infty }(a_{k} + b_{k})=\sum\limits_{k\,=\,1}^{\infty }a_{k} + \sum\limits_{k\,=\,1}^{\infty }b_{k}=S + T }} \] \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,1}^{\infty }(a_{k} - b_{k})=\sum\limits_{k\,=\,1}^{\infty }a_{k} - \sum\limits_{k\,=\,1}^{\infty }b_{k}=S - T }} \]

THEOREM Constant Multiple of a Series

Let \(c\) be a nonzero real number. If \(\sum\limits_{k\,=\,1}^{\infty }a_{k}=S\) is a convergent series, then the series \(\sum\limits_{k\,=\,1}^{\infty }(ca_{k})\) also converges. Moreover, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,1}^{\infty }(ca_{k})=c\sum\limits_{k\,=\,1}^{\infty}a_{k}=cS }} \]

If the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) diverges, then the series \(\sum\limits_{k\,=\,1}^{\infty} (ca_{k})\) also diverges.

IN WORDS

Multiplying each term of a series by a nonzero constant does not affect the convergence (or divergence) of the series.

Using Properties of Series

Determine whether each series converges or diverges. If it converges, find its sum.

1. \(\sum\limits_{k\,=\,4}^{\infty }\dfrac{1}{k} \)
2. \(\sum\limits_{k\,=\,1}^{\infty}\dfrac{2}{k}\)
3. \(\sum\limits_{k\,=\,1}^{\infty }\,\left( \dfrac{1}{2^{k-1}}+\dfrac{1}{3^{k-1}}\right) \)

Solution (a) Except for the first three terms, the series \( \sum\limits_{k\,=\,4}^{\infty }\dfrac{1}{k}=\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{ 1}{6}+\cdots\) is identical to the harmonic series, which diverges. So, it follows that \(\sum\limits_{k\,=\,4}^{\infty }\dfrac{1}{k}\) also diverges.

(b) \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{2}{k}\,{=}\,\sum\limits_{k\,=\,1}^{\infty }\,\left(2\cdot \dfrac{1}{k}\right)\). Since the harmonic series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k}\) diverges, the series \(\sum\limits_{k\,=\,1}^{\infty }\,\left( 2\cdot \dfrac{1}{k}\right)=\sum\limits_{k\,=\,1}^{\infty }\dfrac{2}{k}\) diverges.

(c) Since the series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{ 2^{k-1}}\) and the series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{3^{k-1}}\) are both convergent geometric series, the series defined by \( \sum\limits_{k\,=\,1}^{\infty }\,\left( \dfrac{1}{2^{k-1}}+\dfrac{1}{3^{k-1}} \right) \) is also convergent. The sum is \[ \sum\limits_{k\,=\,1}^{\infty }\,\left( \dfrac{1}{2^{k-1}}+\dfrac{1}{3^{k-1}} \right) =\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{2^{k-1}} +\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{3^{k-1}}=\frac{1}{1-\dfrac{1}{2}}+ \frac{1}{1-\dfrac{1}{3}}=2+\frac{3}{2}=\dfrac{7}{2} \]

NOW WORK

Problem 39.

THEOREM General Convergence Test

An infinite series of positive terms converges if and only if its sequence of partial sums is bounded. The sum of such an infinite series will not exceed an upper bound.

NEED TO REVIEW?

Improper Integrals are discussed in Section 7.8, pp. 523-29.

THEOREM Integral Test

Let \(f\) be a function that is continuous, positive, and decreasing on the interval \([1,\infty)\). Let \( a_{k}=f(k)\) for all positive integers \(k\). Then the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) converges if and only if the improper integral \(\int_{1}^{\infty}f(x)\,dx\) converges.

Using the Integral Test

Determine whether the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}= \sum\limits_{k\,=\,1}^{\infty}\dfrac{4}{k^{2}+1}\) converges or diverges.

Solution The function \(f(x)=\dfrac{4}{x^{2}+1}\) is defined on the interval \([1,\infty) \) and is continuous, positive, and decreasing for all numbers \(x\geq 1\). Also, \(a_{k}=f(k)\) for all positive integers \(k.\) Using the Integral Test, we find \[ \begin{eqnarray*} \int_{1}^{\infty }\!\dfrac{4}{x^{2}+1}\,dx\! : \lim_{b\,\rightarrow \,\infty }\int_{1}^{b}\dfrac{4}{x^{2}+1}\,dx&=&\lim_{b\,\rightarrow \,\infty } \,\left[ 4\int_{1}^{b}\dfrac{1}{x^{2}+1}\,dx\right] =4\lim_{b\,\rightarrow \,\infty }\,\left[\tan ^{-1}x\right] _{1}^{b} \\[12pt] &=& 4\lim_{b\,\rightarrow \,\infty }\,\left[\tan ^{-1}b-\tan ^{-1}1\right]\! =4\,\left[\dfrac{\pi }{2}-\dfrac{\pi }{4}\right]\! =\pi \end{eqnarray*} \]

Since the improper integral converges, the series \(\sum\limits_{k\,=\,1}^{\infty}\dfrac{4}{k^{2}+1}\) converges.

CAUTION

In Example 3 the fact that \(\int_{1}^{\infty }\dfrac{4}{ x^{2}+1}\,dx= \pi\) does not mean that the sum \(S\) of the series is \(\pi \). Do not confuse the value of the improper integral \(\int_{1}^{\infty }f(x) \,dx\) with the sum \(S\) of the series. In general, they are not equal.

Using the Integral Test

Determine whether the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}=\) \( \sum\limits_{k=1}^{\infty }\dfrac{2k}{k^{2}+1}\) converges or diverges.

Solution The function \(f(x)=\dfrac{2x}{x^{2}+1}\) is continuous, positive, and decreasing since \(f' (x) \le 0\) for all numbers \(x\,{\geq}\,1\), and \(a_{k}\,{=}\,f(k)\) for all positive integers \(k.\) Using the Integral Test, we find \[ \begin{eqnarray*} \int_{1}^{\infty }\frac{2x}{x^{2}+1}\,dx\! : \lim_{b\,\rightarrow \,\infty }\int_{1}^{b}\frac{2x}{x^{2}+1}\,dx&=&\lim_{b\,\rightarrow \,\infty }\,\left[\ln (x^{2}+1)\right] _{1}^{b} \\[8pt] &=& \lim_{b\,\rightarrow \,\infty }\,[\ln(b^{2}+1)-\ln 2] =\infty \end{eqnarray*} \]

Since the improper integral diverges, the series \(\sum\limits_{k=1}^{\infty}\dfrac{2k}{k^{2}+1}\) also diverges.

NOW WORK

Problem 21.

Using the Integral Test

Determine whether the series \(\sum\limits_{k\,=2}^{\infty }\dfrac{1}{k(\ln k) ^{2}}\) converges or diverges.

Solution The function \(f(x)\,{=}\,\dfrac{1}{x (\ln x)^{2}}\) is continuous, positive, and decreasing on the interval \([2,\infty)\). Also \(\dfrac{1}{k(\ln k) ^{2}}\,{=}\,f(k) \) for all integers greater than or equal to \(2.\) Using the Integral Test, we investigate the improper integral \(\int_{2}^{\infty }\dfrac{dx}{x(\ln x)^{2} }.\) We find an antiderivative of \(\dfrac{1}{x(\ln x) ^{2}}\) by using the substitution \(u=\ln x,\) \(du=\dfrac{1}{x}dx.\) Then, \[ \int \frac{dx}{x(\ln x)^{2}}=\int \frac{du}{u^{2}}=-\frac{1}{u}+C=-\frac{1 }{\ln x}+C \]

Now we find the improper integral \[ \int_{2}^{\infty }\frac{dx}{x(\ln x)^{2}}\!:\,\,\lim_{b\,\rightarrow \,\infty }\,\left[ -\frac{1}{\ln x} \right] _{2}^{b}=\lim_{b\, \rightarrow \,\infty }\,\left( -\frac{1}{\ln b}\right) +\frac{1}{\ln 2}=\frac{1 }{\ln 2} \]

Since the improper integral \(\int_{2}^{\infty }\dfrac{dx}{x(\ln x)^{2}}\) converges, the series \(\sum\limits_{k\,=2}^{\infty }\dfrac{1}{k(\ln k) ^{2}}\) converges.

NOW WORK

Problem 27.

spanDEFINITIONspan \(p\)-series

A p-series is an infinite series of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k=1}^{\infty }\dfrac{1}{k^{p}}=1+\dfrac{1}{2^{p}}+\dfrac{1}{3^{p}}+\cdots +\dfrac{1}{n^{p}}+\cdots }} \]

where \(p\) is a positive real number.

THEOREM Convergence/Divergence of a \(p\)-Series

The p-series \[ \sum_{k=1}^{\infty }\frac{1}{k^{p}}=1+\frac{1}{2^{p}}+\frac{1}{3^{p}}+\cdots +\frac{1}{n^{p}}+\cdots \]

converges if \(p>1\) and diverges if \(0<p\leq 1\).

Proof

The function \(f(x)=\dfrac{1}{x^{p}},\) \(p>0\), is continuous, positive, and decreasing for all numbers \(x\geq 1\), and \( f(k) =\dfrac{1}{k^{p}}\) for all positive integers \(k.\) So, the series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}\) converges if and only if the improper integral \(\int_{1}^{\,\infty }\dfrac{1}{x^{p}}\,dx\) converges.

In Section 7.8, page 526, we proved that \(\int_{1}^{\,\infty }\dfrac{ dx}{x^{p}}\) converges if \(p>1\) and diverges if \(p\leq 1.\) So, the p-series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}\) converges if \(p>1\) and diverges if \(0<p\leq 1\).

Analyzing a \(p\)-Series

1. The series \[ \sum_{k\,=\,1}^{\infty }\frac{1}{k^{3}}=1+\frac{1}{2^{3}}+\frac{1}{3^{3}} +\cdots +\frac{1}{n^{3}}+\cdots \] converges, since it is a \(p\)-series where \(p=3\).
2. The series \[ \sum_{k\,=\,1}^{\infty }\frac{1}{\sqrt{k}}=1+\frac{1}{\sqrt{2}}+\frac{1}{ \sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}+\cdots \] diverges, since it is a \(p\)-series where \(p=\dfrac{1}{2}\).

NOW WORK

Problem 35.

IN WORDS

The corollary provides an interval of width \(1\) that contains the sum of a convergent \(p\)-series. But it gives no information about the actual sum.

COROLLARY Bounds for the Sum of a Convergent \(p\)-Series

If \(p>1\), then  \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{1}{p-1}<\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}<1+\dfrac{1}{p-1}} } \]

Proof

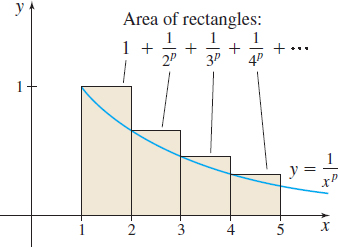
From Figure 19 we have \[ \begin{equation*} \left(\hbox{Area under the graph of } y=\frac{1}{x^{p}}\right) =\int_{1}^{\,\infty }\frac{dx}{x^{p}}< 1 + \frac{1}{2^{p}} + \frac{1}{3^{p}} + \cdots =\sum\limits_{k\,=\,1}^{\infty }\frac{1}{k^{p}} \tag{1} \end{equation*} \]

Figure 19

From Figure 20 we have \[ \begin{equation*} \hbox{1} + \left(\hbox{Area under the graph of}\, y = \frac{1}{x^{p}}\right) = 1 + \int_{1}^{\,\infty }\frac{dx}{x^{p}}> 1 + \frac{1}{2^{p}} + \frac{1}{3^{p}} + \cdots = \sum\limits_{k\,=\,1}^{\infty }\frac{1}{k^{p}} \tag{2} \end{equation*} \]

Combining (1) and (2), we have \[ \begin{equation*} \int_{1}^{\,\infty }\frac{dx}{x^{p}} < \sum\limits_{k\,=\,1}^{\infty }\frac{1}{k^{p}} < 1 + \int_{1}^{\,\infty }\frac{dx}{x^{p}} \tag{3} \end{equation*} \]

Since \(p>1\), \[ \begin{eqnarray*} \int_{1}^{\,\infty }\frac{dx}{x^{p}}=\lim_{b\,\rightarrow \,\infty }\int_{1}^{b}\frac{dx}{x^{p}}=\lim_{b\,\rightarrow \,\infty } \,\bigg[\frac{x^{-p+1}}{-p+1}\bigg]^{b}_{1} = \lim_{b\,\rightarrow \,\infty } \frac{b^{1-p}-1}{1-p} \underset{\underset{\color{#0066A7}{\hbox{\(p\, > \,1\)}}}{\color{#0066A7}{\uparrow}}}{=} \frac{0-1}{1-p} = \frac{1}{p-1} \end{eqnarray*} \]

Using this result in (3), we get \[ \frac{1}{p-1}<\sum_{k\,=\,1}^{\infty }\frac{1}{k^{p}}<1+\frac{1}{p-1} \]

Figure 20

Proof of the Integral Test

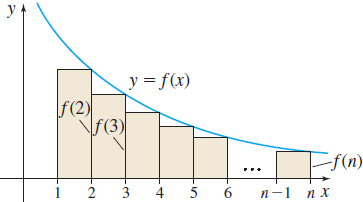
Suppose \(\int_{1}^{\infty}f(x)\,dx\) converges. Then \(\lim\limits_{n\,\rightarrow \,\infty }\int_{1}^{n}f(x)\,dx\) exists and equals some number \(L\). As Figure 21 shows, \(\int_{1}^{n}f(x)\,dx\) underestimates the area under the graph of \(f\) on \([1,\infty).\) As a result, \[ \int_{1}^{n}\,f(x)dx<L \qquad \hbox{for any number }n \]

But \(f\) is decreasing on the interval \([1,n]\). So, the sum of the areas of the \(n-1\) rectangles drawn in Figure 21 underestimates the area under the graph of \(y=f(x)\) from \(1\) to \(n\). That is, \[ f(2)+f(3)+\cdots +f(n)<\int_{1}^{n}f(x)\,dx <L \]

Now add \(f(1)=a_{1}\) to each part, and use the fact that \(a_{1}=f(1),\) \( a_{2}=f(2),\) \(\ldots ,\) \(a_{n}=f(n)\). Then \[ a_{1}+a_{2}+a_{3}+\cdots +a_{n}=f(1)+f(2)+\cdots +f(n)<f(1)\,{+}\,\!\int_{1}^{n}f(x)dx<f(1)+L \]

This means that the partial sums of \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) are bounded from above. Since the partial sums are also increasing, \( \sum\limits_{k\,=\,1}^{\infty }a_{k}\) converges.

Figure 22

Now suppose \(\int_{1}^{\infty }\,f(x)\,dx\) diverges. Since \(f\) is decreasing on \([1,n]\), the sum of the areas of the \(n-1\) rectangles shown in Figure 22 overestimates the area under the graph of \(y=f(x)\) from \(1\) to \(n\). That is, \[ f(1)+f(2)+\cdots +f(n-1)>\int_{1}^{n}f(x)\,dx \]

Since \(\int_{1}^{n}f(x)\,dx \rightarrow \infty \)  as \(n\rightarrow \infty ,\) the \(n\)th partial sum \(S_{n}\) must also approach infinity, and it follows that the series \(\sum\limits_{k\,=\,1}^{\infty }a_{k}\) diverges.