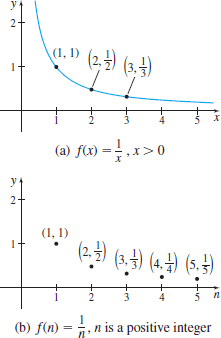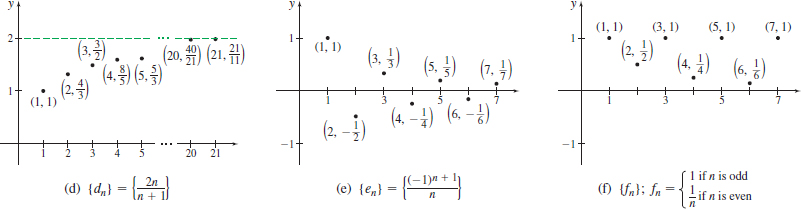8.1 SequencesPrinted Page 538
538
OBJECTIVES
When you finish this section, you should be able to:
NEED TO REVIEW?
Sequences are discussed in Appendix A.5, pp. A-38 to A-39.
The study of infinite sums of numbers has important applications in physics and engineering since it provides an alternate way of representing functions. In particular, infinite series may be used to approximate irrational numbers, such as e, π, and ln2. The theory of infinite series is developed through the use of a special kind of function called a sequence.
DEFINITION
A sequence is a function whose domain is the set of positive integers and whose range is a subset of the real numbers.
To get an idea of what this means, consider the graph of the function f(x)=1x for x>0, as shown in Figure 1(a). If all the points on the graph are removed except the points (1,1), (2,12), (3,13), and so on, as shown in Figure1(b), then these points are the graph of a sequence. Notice the graph consists of points, one point for each positive integer.
A sequence is often represented by listing its values in order. For example, the sequence in Figure 1(b) can be written as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{f(1)\hbox{, }f(2)\hbox{, }f(3)\hbox{, }f(4)\hbox{, }f(5) , \ldots}}
or as the list \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, \ldots}}
The list never ends, as the three dots at the end (called ellipsis) indicate. The numbers in the list are called the terms of the sequence. Using subscripted letters to represent the terms of a sequence, this sequence can be written as s_{1}=f(1)=1 \qquad s_{2}=f(2)=\dfrac{1}{2} \qquad s_{3}=f(3)=\dfrac{1}{3}\ldots \qquad s_{n}=f(n)=\dfrac{1}{n}\ldots
IN WORDS
\{s_{n}\}_{n=1}^{\infty}=\left\{ \dfrac{1}{n}\right\} _{n=1}^{\infty } or \{s_{n}\}=\left\{\dfrac{1}{n}\right\} is the name of the sequence; s_{n}=\dfrac{1}{n} is the nth term of the sequence.
It is easy to obtain any term of this sequence because s_{n}=f(n)=\dfrac{1}{n}. In general, whenever a rule for the n{\bf th} \, \textbf{term} of a sequence is known, then any term of the sequence can be found. We also use the nth term to identify the sequence. When the nth term is enclosed in braces, it represents the sequence. The notation \{s_{n}\}=\left\{ \dfrac{1}{n}\right\} or \{ s_{n}\} _{n=1}^{\infty }=\left\{\dfrac{1}{n}\right\} _{n=1}^{\infty } both represent the sequence 1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, \ldots.
1 Write the Terms of a SequencePrinted Page 539
539
EXAMPLE 1Writing the Terms of a Sequence
Write the first three terms of each sequence:
- (a) \{b_{n}\} _{n=1}^{\infty }=\left\{ \dfrac{1}{3n-2}\right\} _{n=1}^{\infty }
- (b) \left\{ c_{n}\right\}=\left\{ \dfrac{2n-1}{n^{3}}\right\}
Solution (a) The nth term of this sequence is b_{n}=\dfrac{1}{3n-2}. The first three terms are b_{1}=\dfrac{1}{3\cdot 1-2}=1\qquad b_{2}=\dfrac{1}{3\cdot 2-2}=\dfrac{1}{4}\qquad b_{3}=\dfrac{1}{3\cdot 3-2}=\dfrac{1}{7}
(b) The nth term of this sequence is c_{n}=\dfrac{2n-1}{n^{3}}. Then c_{1}=\dfrac{2(1)-1}{1^{3}}=1\qquad c_{2}=\dfrac{2(2) -1}{2^{3}}=\dfrac{3}{8}\qquad c_{3}=\dfrac{2 (3) -1}{3^{3}}=\dfrac{5}{27}
NOW WORK
For simplicity, from now on we use the notation \{ s_{n}\}, rather than \{ s_{n}\} _{n=1}^{\infty }, to represent a sequence.
EXAMPLE 2Writing the Terms of a Sequence
Write the first five terms of the sequence \{a_{n}\} =\left\{ (-1)^{n}\left( \dfrac{1}{2}\right) ^{n}\right\}
Solution The nth term of this sequence is a_{n}=(-1)^{n}\left(\dfrac{1}{2}\right) ^{n}. So, \begin{eqnarray*} a_{1}&=&(-1)^{1}\left(\dfrac{1}{2}\right) ^{1}=-\dfrac{1}{2}\quad a_{2}=(-1)^{2}\left(\dfrac{1}{2}\right) ^{2}=\dfrac{1}{4}\quad a_{3}=(-1)^{3}\left(\dfrac{1}{2}\right) ^{3}=-\dfrac{1}{8}\\[6pt] a_{4}&=&\dfrac{1}{16}\quad a_{5}=-\dfrac{1}{32} \end{eqnarray*}
The first five terms of the sequence \{a_{n}\} are -\dfrac{1}{2}, \dfrac{1}{4}, -\dfrac{1}{8}, \dfrac{1}{16}, -\dfrac{1}{32}.
Notice the terms of the sequence \{a_{n}\} given in Example 2 alternate between positive and negative due to the factor (-1)^{n}, which equals -1 when n is odd and equals 1 when n is even. Sequences of the form \{(-1) ^{n}a_{n}\}, \{(-1) ^{n-1}a_{n}\}, or \{(-1)^{n+1}a_{n}\}, where a_{n}>0 for all n, are called alternating sequences.
NOW WORK
2 Find the nth Term of a SequencePrinted Page 539
The rule defining a sequence \{s_{n}\} is often expressed by an explicit formula for its nth term s_{n}, There are times, however, when a sequence is indicated using the first few terms, suggesting a natural choice for the nth term.
540
EXAMPLE 3Finding the nth Term of a Sequence
Find the nth term of each of the following sequences. Assume that the indicated patterns continue.
Solution
| Sequence | nth term |
|---|---|
| (a) \, \, e, \dfrac{e^{2}}{2},\dfrac{e^{3}}{3},\ldots | a_{n}=\dfrac{e^{n}}{n} |
| (b) \, \, 1,\dfrac{1}{3},\,\dfrac{1}{9},\,\dfrac{1}{27},\ldots | b_{n}=\left( \dfrac{1}{3}\right) ^{n-1} |
| (c) \, \, 1,\,4,\,9,\,16,\,25,\,\ldots | c_{n}=n^{2} |
| (d) \, \, \dfrac{2}{2},\,\dfrac{4}{3}, \dfrac{6}{4}, \dfrac{8}{5},\,\ldots | d_{n}=\dfrac{2n}{n+1} |
| (e) \, \, 1,\,-\dfrac{1}{2},\,\dfrac{1}{3},\,-\dfrac{1}{4},\,\dfrac{1}{5},\,\ldots | e_{n}=\dfrac{(-1)^{n+1}}{n} |
| (f) \, \, 1,\,\dfrac{1}{2},\,1,\,\dfrac{1}{4},\,1,\,\dfrac{1}{6},\ldots | f_{n}=\left\{\begin{array}{lll} 1 &\hbox{if } n\hbox{ is odd} \\ \dfrac{1}{n} &\hbox{if } n\hbox{ is even} \end{array}\right. |
The graphs of the sequences (d)–(f) are given in Figure 2.
NOW WORK
Convergent Sequences
As we look from left to right, the points of the graph of the sequence \left\{ d_{n}\right\} =\left\{ \dfrac{2n}{n+1}\right\} in Figure 2(d) get closer to the line y=2. If we could look far enough to the right, the points would appear to be on the line y=2 (although, in reality, the points are always some very small distance below the line). In fact, as Table 1 suggests, \dfrac{2n}{n+1} can be made as close as we please to 2 by taking n sufficiently large.
| n | 1 | 9 | 99 | 999 | 9999 | 999,999 |
| d_{n}=\dfrac{2n}{n+1} | 1 | 1.8 | 1.98 | 1.998 | 1.9998 | 1.999998 |
We describe this behavior by saying that the sequence \left\{d_{n}\right\} =\left\{ \dfrac{2n}{n+1}\right\} converges to 2, and we write \ \lim\limits_{n\,\rightarrow \,\infty }\dfrac{2n}{n+1}=2.
541
DEFINITION Convergent Sequence
Let L be a real number and let \{ s_{n}\} be a sequence. The sequence \{ s_{n}\} converges to a real number L if, for any number \varepsilon >0, there is a positive integer N so that \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\left\vert s_{n}-L\right\vert <\varepsilon \qquad \hbox{for all integers}\, n>N}}
If \{ s_{n}\} converges to L, then L is called the limit of the sequence and we write \lim\limits_{n\rightarrow \infty}s_{n}=L. If a sequence converges, it is said to be convergent; otherwise, it is said to be divergent.
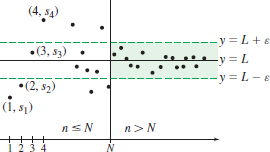
Figure 3 provides a geometric interpretation of the statement \lim\limits_{n\,\rightarrow \,\infty }s_{n}=L. The figure also illustrates that the beginning terms of a sequence do not affect the convergence (or divergence) of the sequence. That is, the beginning terms of a sequence can be ignored when determining convergence or divergence.
When n\leq N, the distance between the point ( n,s_{n}) and the line y=L may or may not be less than \varepsilon ; these terms have no effect on the convergence or divergence of the sequence. For any \varepsilon >0, there is an integer N so that for all n>N, the distance between the point (n,s_{n}) and the line y=L remains less than \varepsilon, that is, \left\vert s_{n}-L\right\vert <\varepsilon for all n>N.
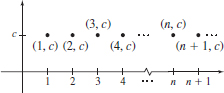
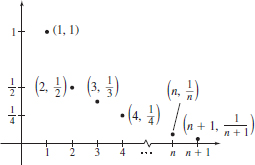
EXAMPLE 4Showing a Sequence Converges
Show that:
- (a) \lim\limits_{n\rightarrow \infty }c=c
- (b) \lim\limits_{n\rightarrow \infty }\dfrac{1}{n}=0
Solution (a) The graph of the sequence \{ s_{n}\} =\{c\} suggests that \{ s_{n}\} converges to c. See Figure 4.
To show the sequence converges to c, we look at \vert s_{n}-c\vert . Then for any \varepsilon >0, \vert s_{n}-c\vert =\left\vert c-c\right\vert =0<\varepsilon \qquad \hbox{ for all }n
The sequence \{ s_{n}\} =\{c\} converges to c.
(b) The graph of the sequence \{s_{n}\} =\left\{\dfrac{1}{n}\right\} shown in Figure 5 suggests that \{ s_{n}\} converges to 0.
To show the sequence \{ s_{n}\} =\left\{ \dfrac{1}{n}\right\} converges to 0, we look at \left\vert s_{n}-0\right\vert =\left\vert \dfrac{1}{n}-0\right\vert =\dfrac{1}{n}
For any \varepsilon > 0, choose any integer N>\dfrac{1}{\varepsilon }. Then for all n>N>\dfrac{1}{\varepsilon }, we have \left\vert s_{n}-0\right\vert =\dfrac{1}{n}<\dfrac{1}{N}<\varepsilon, so the sequence \{ s_{n}\} =\left\{ \dfrac{1}{n}\right\} converges to 0.
542
We state, without proof, some properties of convergent sequences.
THEOREM Properties of Convergent Sequences
If \{ s_{n}\} and \{ t_{n}\} are convergent sequences and if c is a number, then
- Constant multiple property: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\,\rightarrow \,\infty}(cs_{n}) =c\lim\limits_{n\,\rightarrow \,\infty }s_{n}}} \tag{1} \end{equation}
- Sum and difference properties: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\,\rightarrow \,\infty }\left( s_{n}\pm t_{n}\right) =\lim\limits_{n\,\rightarrow \,\infty }s_{n}\pm\lim\limits_{n\,\rightarrow \,\infty }t_{n}}} \tag{2} \end{equation}
- Product property: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\,\rightarrow \,\infty }(s_{n}\cdot t_{n}) =\left( \lim\limits_{n\,\rightarrow \,\infty }s_{n}\right) \left(\lim\limits_{n\,\rightarrow \,\infty }t_{n}\right) \hspace{-1pt}}} \tag{3} \end{equation}
- Quotient property: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\,\rightarrow \,\infty }\dfrac{s_{n}}{t_{n}}=\dfrac{\lim\limits_{n\,\rightarrow \,\infty }s_{n}}{\lim\limits_{n\,\rightarrow \,\infty }t_{n}}\quad \hbox{ provided } \quad \lim\limits_{n\,\rightarrow \,\infty }t_{n}\neq 0}} \tag{4} \end{equation}
- Power property: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\rightarrow \infty }s_{n}^{p}=\left[ \lim\limits_{n\rightarrow \infty }s_{n}\right]^{p}\qquad p\geq 2 \hbox{ is an integer }\hspace{-1.5pt}}} \tag{5} \end{equation}
- Root property: \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\lim\limits_{n\rightarrow \infty }\sqrt[p]{s_{n}}=\sqrt[p]{\lim\limits_{n\rightarrow \infty }s_{n}}\qquad p\geq 2 \hbox{ and }s_{n}\geq 0 \hbox{ if } p \hbox{ is even}}} \tag{6} \end{equation}
3 Use Properties of Convergent SequencesPrinted Page 542
EXAMPLE 5Using Properties of Convergent Sequences
Use properties of convergent sequences to find \lim\limits_{n\rightarrow \infty }s_{n}.
- (a) \{ s_{n}\} =\left\{ \dfrac{2}{n}+3\right\}
- (b) \{ s_{n}\} =\left\{\dfrac{4}{n^{2}}\right\}
- (c) \{ s_{n}\} =\left\{ \sqrt[3]{\dfrac{16n^{2}+3n}{2n^{2}}}\right\}
Solution
(a) \begin{eqnarray*} \lim\limits_{n\rightarrow \infty}s_{n}&=&\lim\limits_{n\rightarrow \infty }\left( \dfrac{2}{n}+3\right)=\lim\limits_{n\rightarrow \infty }\dfrac{2}{n}+\lim\limits_{n\rightarrow\infty }3\\ &=&2\lim\limits_{n\rightarrow \infty }\dfrac{1}{n}+\lim\limits_{n\rightarrow \infty }3 \underset{\underset{\color{#0066A7}{\lim\limits_{n\rightarrow \infty}\dfrac{1}{n}=0;\,\,\lim\limits_{n\rightarrow\infty} 3=3}}{\color{#0066A7}{\uparrow}}}{=} 2\cdot 0+3=3\\ \end{eqnarray*}
(b) \begin{eqnarray*} \lim\limits_{n\rightarrow \infty }s_{n}=\lim\limits_{n\rightarrow \infty }\dfrac{4}{n^{2}}=4\lim\limits_{n\rightarrow \infty }\dfrac{1}{n^{2}}=4\lim\limits_{n\rightarrow \infty }\dfrac{1}{n}\cdot \lim\limits_{n\rightarrow \infty }\dfrac{1}{n} \underset{\underset{\color{#0066A7}{\lim\limits_{n\rightarrow \infty }\dfrac{1}{n}=0}}{\color{#0066A7}{\uparrow}}}{=} 4\cdot 0\cdot 0=0\\ \hspace{-7pc} \end{eqnarray*}
543
(c) \begin{eqnarray*} \lim\limits_{n\rightarrow \infty}s_{n} &=&\lim\limits_{n\rightarrow \infty }\sqrt[3]{\dfrac{16n^{2}+3n}{2n^{2}}}=\sqrt[3]{\lim\limits_{n\rightarrow \infty }\left( \dfrac{16n^{2}+3n}{2n^{2}} \right) }=\sqrt[3]{\lim\limits_{n\rightarrow \infty }\left( 8+\dfrac{3}{2n}\right) }\\ &=&\sqrt[3]{\lim\limits_{n\rightarrow \infty }8+\lim\limits_{n\rightarrow \infty }\dfrac{ 3}{2n}} \underset{\underset{\color{#0066A7}{\lim\limits_{n\rightarrow \infty }8=8}}{\color{#0066A7}{\uparrow}}}{=} \sqrt[3]{8+\dfrac{3}{2}\lim\limits_{n\rightarrow \infty } \dfrac{1}{n}} \underset{\underset{\color{#0066A7}{\lim\limits_{n\rightarrow \infty }\dfrac{1}{n}=0}}{\color{#0066A7}{\uparrow}}}{=} \sqrt[3]{8+\dfrac{3}{2}\cdot 0}=\sqrt[3]{8}=2 \\ \end{eqnarray*}
NOW WORK
The next result is also useful for showing a sequence converges. You are asked to prove it in Problem 136.
THEOREM
Let \{ s_{n}\} be a sequence of real numbers. If \lim\limits_{n\rightarrow \infty }s_{n}=L and if f is a function that is continuous at L and is defined for all numbers s_{n}, then \lim\limits_{n\rightarrow \infty }f( s_{n}) =f(L).
EXAMPLE 6Showing a Sequence Converges
Show \left\{\ln \left(\dfrac{2}{n}+3\right) \right\} converges and find its limit.
Solution Since \lim\limits_{n\rightarrow \infty }\left( \dfrac{2}{n}+3\right) =3 [from Example 5(a)], the sequence \{ s_{n}\}=\left\{ \dfrac{2}{n}+3\right\} converges to 3. The function f(x) =\ln x is continuous on its domain, so it is continuous at 3. Then \lim\limits_{n\rightarrow \infty }f( s_{n}) =\lim\limits_{n\rightarrow \infty }f \left( \dfrac{2}{n}+3\right) =\lim\limits_{n\rightarrow \infty }\ln \left( \dfrac{2}{n}+3\right) =\ln\left[\lim\limits_{n\rightarrow \infty } \left(\dfrac{2}{n}+3\right) \right] =\ln 3
So, the sequence \left\{\ln \left( \dfrac{2}{n}+3\right) \right\} converges to \ln 3.
NOW WORK
4 Use a Related Function or the Squeeze Theorem to Show a Sequence ConvergesPrinted Page 543
Sometimes a sequence \{ s_{n}\} can be associated with a related function f, which can be helpful in determining whether the sequence converges.
DEFINITION Related Function of a Sequence
A related function f of the sequence \{s_{n}\} has the following two properties:
- f is defined on the open interval (0,\,\infty); that is, the domain of f is the set of positive real numbers.
- f(n) =s_{n} for all integers n\geq 1.
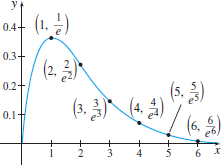
EXAMPLE 7Identifying a Related Function of a Sequence
If \{ s_{n}\} =\left\{\dfrac{n}{e^{n}}\right\}, then a related function is given by f(x)=\dfrac{x}{e^{x}}, where x>0, as shown in Figure 6.
There is a connection between the convergence of certain sequences \{ s_{n}\} and the behavior at infinity of a related function f of the sequence \{ s_{n}\}. The following result, which we state without proof, explains this connection.
544
THEOREM
Let \{ s_{n}\} be a sequence of real numbers and let f be a related function of \{ s_{n}\} .Suppose L is a real number. \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\hbox{If } \lim\limits_{x\,\rightarrow \,\infty } f(x)=L\qquad \hbox{ then}\quad \lim\limits_{n\,\rightarrow \,\infty }s_{n}=L} }\tag{7} \end{equation}
NEED TO REVIEW?
Limits at infinity are discussed in Section 1.5, pp. 117-125.
EXAMPLE 8Using a Related Function to Show a Sequence Converges
Show that \left\{{\dfrac{3n^{2}+5n-2}{6n^{2}-6n+5}}\right\} converges and find its limit.
Solution The function f(x)= \dfrac{3x^{2}+5x-2}{6x^{2}-6x+5} \quad x>0
is a related function of the sequence \left\{ \dfrac{3n^{2}+5n-2}{6n^{2}-6n+5}\right\}. Since \begin{eqnarray*} \lim\limits_{x\,\rightarrow \,\infty }\,f(x)&=&\lim_{ x \rightarrow \,\infty }\frac{3x^{2}+5x-2}{6x^{2}-6x+5} =\lim_{ x \rightarrow \,\infty }\frac{\dfrac{3x^{2}}{6x^{2}}+\dfrac{5x}{6x^{2}}-\dfrac{2}{6x^{2}}}{1-\dfrac{6x}{6x^{2}}+\dfrac{5}{6x^{2}}}\\[5pt] &=&\lim_{x\rightarrow \,\infty }\frac{\dfrac{1}{2}+\dfrac{5}{6x}-\dfrac{1}{3x^{2}}}{1-\dfrac{1}{x}+\dfrac{5}{6x^{2}}}=\dfrac{\dfrac{1}{2}+0-0}{1-0+0}=\dfrac{1}{2} \end{eqnarray*}
the sequence \left\{ \dfrac{3n^{2}+5n-2}{6n^{2}-6n+5}\right\} converges and \lim\limits_{n\,\rightarrow \,\infty } \dfrac{3n^{2}+5 n-2}{6n^{2}-6n+5}=\dfrac{1}{2}.
NOW WORK
We can sometimes find the limit of a sequence \{ s_{n}\} by applying L’Hôpital’s Rule to its related function f, provided f meets the necessary requirements.
NEED TO REVIEW?
L’Hôpital’s Rule is discussed in Section 4.5, pp. 299-302.
EXAMPLE 9Using L’Hôpital’s Rule to Show a Sequence Converges
Show that \left\{ \dfrac{n}{e^{n}}\right\} converges and find its limit.
Solution We begin with the related function f(x)=\dfrac{x}{e^{x}}, x>0. To find \lim\limits_{x\rightarrow \infty }f(x), we use L’Hôpital’s Rule. \begin{eqnarray*} \lim_{x\,\rightarrow \,\infty }\,f(x) &=& \lim_{x\,\rightarrow \,\infty }\frac{x}{e^{x}} \underset{\underset{\color{#0066A7}{\rm Use L’Hôpital’s Rule}}{\color{#0066A7}{\uparrow}}}{=} \lim_{x\,\rightarrow\,\infty }\frac{1}{e^{x}}=0 \\[-8pt] \end{eqnarray*}
Since \lim\limits_{x\,\rightarrow \,\infty }\,f(x)=0, the sequence \left\{ \dfrac{n}{e^{n}}\right\} converges and \lim\limits_{n\,\rightarrow \,\infty}\dfrac{n}{e^{n}}=0.
NOW WORK
Be careful! A related function f can be used to show a sequence \{ s_{n}\} converges only if \lim\limits_{x\,\rightarrow \,\infty} f(x)=L, where L is a real number. If \lim\limits_{x\,\rightarrow \,\infty } f(x) is infinite, then \{ s_{n}\} diverges. If \lim\limits_{x\rightarrow \infty }f(x) does not exist, then we cannot use the theorem relating \lim\limits_{n\,\rightarrow \,\infty}s_{n} and \lim\limits_{x\,\rightarrow \,\infty } f(x).
NEED TO REVIEW?
The Squeeze Theorem for functions is discussed in Section 1.4, pp. 106-107.
545
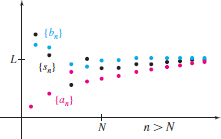
THEOREM The Squeeze Theorem for Sequences
Suppose \{a_{n}\}, \{b_{n}\}, and \{ s_{n}\} are sequences and N is a positive integer. If a_{n}\leq s_{n}\leq b_{n} for every integer n>N, and if \lim\limits_{n\rightarrow \infty }a_{n}=\lim\limits_{n\rightarrow \infty }b_{n}=L, then \lim\limits_{n\rightarrow \infty }s_{n}=L.
Figure 7 illustrates the Squeeze Theorem for sequences.
EXAMPLE 10Using the Squeeze Theorem for Sequences
Show that \{ s_{n}\} =\left\{(-1) ^{n}\dfrac{1}{n}\right\} converges and find its limit.
Solution We seek two sequences that "squeeze" \{ s_{n}\} = \left\{ (-1) ^{n}\dfrac{1}{n}\right\} as n becomes large. We begin with \vert s_{n}\vert: \begin{eqnarray*} \vert s_{n}\vert &=&\left\vert (-1) ^{n}\dfrac{1}{n}\right\vert \leq \dfrac{1}{n} \\[5pt] -\dfrac{1}{n} &\leq &(-1) ^{n}\dfrac{1}{n}\leq \dfrac{1}{n} \end{eqnarray*}
Notice that s_{n} is bounded by \{a_{n}\} =\left\{ -\dfrac{1}{n}\right\} and \{b_{n}\} =\left\{ \dfrac{1}{n}\right\}. Since a_{n}\leq s_{n}\leq b_{n} for all n and \lim\limits_{n\rightarrow \infty }a_{n}=\lim\limits_{n\rightarrow \infty }\left( -\dfrac{1}{n}\right) =0, and \lim\limits_{n\rightarrow \infty }b_{n}=\lim\limits_{n\rightarrow \infty }\dfrac{1}{n}=0, then by the Squeeze Theorem, the sequence \{ s_{n}\} =\left\{ (-1) ^{n}\dfrac{1}{n}\right\} converges and \lim\limits_{n\rightarrow \infty } s_n=0 .
NOW WORK
5 Determine Whether a Sequence Converges or DivergesPrinted Page 545
A sequence \{ s_{n}\} diverges if \lim\limits_{n\rightarrow \infty } s_{n} does not exist. This can happen if
- there is no single number L that the terms of the sequence approach as n\rightarrow \infty
- \lim\limits_{n\,\rightarrow \,\infty } s_{n} = \infty
DEFINITION Divergence of a Sequence to Infinity
The sequence \{ s_{n}\} diverges to infinity, that is, \lim_{n\rightarrow \infty }s_{n}=\infty
if, given any positive number M, there is a positive integer N so that whenever n>N, then s_{n}>M.
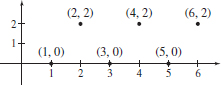
EXAMPLE 11Showing a Sequence Diverges
Show that the following sequences diverge:
- (a) \{1+(-1)^{n}\}
- (b) \{n\}
Solution (a) The terms of the sequence are 0, 2, 0, 2, 0, 2, \ldots \,. See Figure 8. Since the terms alternate between 0 and 2, the terms of the sequence \{1+(-1)^{n}\} do not approach a single number L. So, the sequence \{1+(-1)^{n}\} is divergent.
546
(b) The terms of the sequence \{ s_{n}\}=\{n\} are 1,\,2,\,3,\,4,\ldots. Given any positive number M, we choose a positive integer N>M. Then whenever n>N, we have s_{n}=n>N>M. That is, the sequence \{n\} diverges to infinity. See Figure 9.
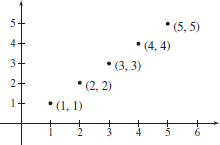
NOW WORK
The next results are useful throughout the chapter. You are asked to prove them in Problems 132–135.
The sequence \{s_n \} = \{ r^{n}\}, where r is a real number,
- converges to 0, if -1<r<1.
- converges to 1, if r=1.
- diverges for all other numbers.
EXAMPLE 12Determine Whether {\{r^{n}\}} Converges or Diverges
Determine whether the following sequences converge or diverge:
- (a) \{ s_{n}\} =\left\{ \left( \dfrac{3}{4}\right) ^{n}\right\}
- (b) \{ t_{n}\} =\left\{\left( \dfrac{4}{3}\right) ^{n}\right\}
Solution (a) The sequence \{ s_{n}\} =\left\{ \left(\dfrac{3}{4}\right) ^{n}\right\} converges to 0 because -1<\dfrac{3}{4}<1.
(b) The sequence \{ t_{n}\} =\left\{ \left( \dfrac{4}{3}\right) ^{n}\right\} diverges because \dfrac{4}{3}>1.
NOW WORK
There are other ways to show that a sequence converges or diverges. To explore these, we need to define a bounded sequence and a monotonic sequence.
Bounded Sequences
A sequence \{ s_{n}\} is bounded from above if every term of the sequence is less than or equal to some number M. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{s_{n}\leq M \qquad \hbox{ for all } n}}
See Figure 10.
Similarly, a sequence \{ s_{n}\} is bounded from below if every term of the sequence is greater than or equal to some number m. That is, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{s_{n}\geq m \qquad \hbox{ for all }n}}
See Figure 11.
For example, since s_{n}=\cos n\leq 1 for all n, the sequence \{ s_{n}\} =\left\{ \cos n\right\} is bounded from above by 1, and since s_{n}=\cos n\geq -1 for all n, \{s_{n}\} is bounded from below by -1.
EXAMPLE 13Determining Whether a Sequence Is Bounded from Above or Bounded from Below
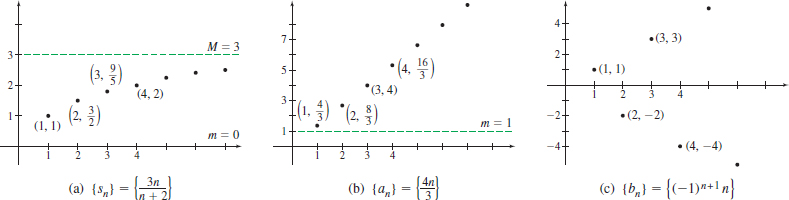
- (a) The sequence \{ s_{n}\} =\left\{ \dfrac{3n}{n+2}\right\} is bounded both from above and below because \dfrac{3n}{n+2}=\dfrac{3}{1+\dfrac{2}{n}}<3 \qquad \hbox{ and }\qquad \dfrac{3n}{n+2}>0 \quad \hbox{ for all } n\geq 1 See Figure 12(a).
547
- (b) The sequence \{a_{n}\} =\left\{ \dfrac{4n}{3}\right\} is bounded from below because \dfrac{4n}{3}>1 for all n\geq 1. It is not bounded from above because \lim\limits_{n\rightarrow \infty }\dfrac{4n}{3}=\dfrac{4}{3}\lim\limits_{n\rightarrow \infty }n=\infty. See Figure 12(b).
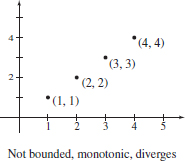
- (c) The sequence \{b_{n}\} =\left\{ (-1)^{n+1}n\right\} is neither bounded from above nor bounded from below.If n is odd, \lim\limits_{n\rightarrow \infty }b_{n} = \lim\limits_{n\rightarrow \infty } n =\infty, and if n is even, \lim\limits_{n\rightarrow \infty }b_{n}= \lim\limits_{n\rightarrow \infty } (-n) = -\infty. See Figure 12(c).
NOW WORK
A sequence \{ s_{n}\} is bounded if it is bounded both from above and from below. For a bounded sequence \{s_{n}\} , there is a positive number K for which \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\vert s_{n}\vert \leq K \qquad \hbox{for all }n\geq 1}}
For example, the sequence \{ s_{n}\} =\left\{ \dfrac{3n}{n+2}\right\} [from Example 13(a)] is bounded, since \left\vert \dfrac{{3n}}{n+2}\right\vert \leq 3 for all integers n\geq 1.
THEOREM Boundedness Theorem
A convergent sequence is bounded.
NEED TO REVIEW?
The Triangle Inequality is discussed in Appendix A.1, p. A-7
Proof
If \{ s_{n}\} is a convergent sequence, there is a number L for which \lim\limits_{n\,\rightarrow \,\infty}s_{n}=L. We use the definition of the limit of a sequence with \varepsilon =1. Then there is a positive integer N so that \left\vert s_{n}-L\right\vert <1 \qquad \hbox{for all }n>N
Then, for all n>N, \begin{eqnarray*} &&\vert s_{n}\vert =\vert s_{n}-L+L \vert \leq \vert s_{n}-L \vert + \vert L \vert <1+ \vert L \vert \\ &&\hspace{0pc} \qquad\qquad \, \underset{\color{#0066A7}{\rm Triangle \, Inequality}}{\color{#0066A7}{\uparrow}} \end{eqnarray*}
If we choose K to be the largest number in the finite collection |s_{1}|,\quad |s_{2}|,\quad |s_{3}|,\quad \ldots ,\quad |s_{N}|,\quad 1+|L|
it follows that \vert s_{n}\vert \leq K for all integers n\geq 1. That is, the sequence \{s_{n}\} is bounded.
A restatement of the boundedness theorem provides a test for divergent sequences.
THEOREM Test for Divergence of a Sequence
If a sequence is not bounded from above or if it is not bounded from below, then it diverges.
CAUTION
The converse of the boundedness theorem is not true. Bounded sequences may converge or they may diverge. For example, the sequence \{1+(-1)^{n}\} in Example 11(a) is bounded, but it diverges.
For example, the sequences \{ -n \}, \left\{ 2^{n}\right\}, and \{\ln n\} are either not bounded from above or not bounded from below, so they are divergent.
548
Monotonic Sequences
DEFINITION
A sequence \{ s_{n}\} is said to be:
- Increasing if s_{n}<s_{n+1} for n\geq 1.
- Nondecreasing if s_{n} \leq s_{n+1} for n\geq 1.
- Decreasing if s_{n} >s_{n+1} for n\geq 1.
- Nonincreasing if s_{n} \geq s_{n+1} for n\geq 1.
If any of the above conditions hold, the sequence is called monotonic.
Table 2 lists three ways to show a sequence \{s_{n}\} is monotonic.
| To Show {\{ s}_{n}\} Is Decreasing | To Show \{ s_{n}\} Is Increasing | |
|---|---|---|
| Algebraic Difference | Show s_{n+1}-s_{n}<0 for all n\geq 1. | Show s_{n+1}-s_{n}>0 for all n\geq 1. |
| Algebraic Ratio | If s_{n}>0 for all n\geq 1, show \dfrac{s_{n+1}}{s_{n}} <1 for all n\geq 1. | If s_{n}>0 for all n\geq 1, show \dfrac{s_{n+1}}{s_{n}}>1 for all n\geq 1. |
| Derivative | Show the derivative of a related function f of \{s_{n}\} is negative for all x\geq 1. | Show the derivative of a related function f of \{s_{n}\} is positive for all x\geq 1. |
These tests can be extended to show a sequence is nonincreasing or nondecreasing.
EXAMPLE 14Showing a Sequence Is Monotonic
Show that each of the following sequences is monotonic by determining whether it is increasing, nondecreasing, decreasing, or nonincreasing:
- (a) \{ s_{n}\} =\left\{ {\dfrac{n}{n+1}}\right\}
- (b) \{ s_{n}\} =\left\{ {\dfrac{e^{n}}{n!}}\right\}
- (c) \{ s_{n}\} =\{\ln n\}
Solution
(a) We use the algebraic difference test. \begin{eqnarray*} s_{n+1}-s_{n} &=& \frac{n+1}{n+2}-\frac{n}{n+1}=\frac{n^{2}+2n+1-n^{2}-2n}{(n+2)(n+1)}\\[5pt] &=&\frac{1}{(n+2)(n+1)}>0 \qquad \hbox{ for all }n\geq 1 \end{eqnarray*}
So, \{ s_{n}\} is an increasing sequence.
(b) When the sequence contains a factorial, the algebraic ratio test is usually easiest to use. \frac{s_{n+1}}{s_{n}}=\frac{\dfrac{e^{n+1}}{(n+1)!}}{\dfrac{e^{n}}{n!}}=\left( {\frac{e^{n+1}}{e^{n}}}\right) \frac{n!}{(n+1)!}=\frac{e}{n+1}<1 \qquad \hbox{ for all }n\geq 2
After the first term, \{ s_{n}\} =\left\{ \dfrac{e^{n}}{n!}\right\} is a decreasing sequence.
(c) Here, we use the derivative of the related function f(x) =\ln x of the sequence \{ s_{n}\} =\{\ln n\}. Since \dfrac{d}{dx}\ln x=\dfrac{1}{x}>0 for all x>0, it follows that f is an increasing function and so the sequence \{\ln n\} is an increasing sequence.
RECALL
n!=n(n-1) (n-2)\cdots 2\cdot 1 So \dfrac{n!}{(n+1)!} =\dfrac{1}{n+1}.
NOW WORK
549
Not every sequence is monotonic. For example, the sequences \{ s_{n}\} =\left\{ \sin \left( \dfrac{\pi }{2}n\right) \right\} and \{ t_{n}\} =\left\{ 1+\dfrac{(-1)^{n}}{n^{2}}\right\}, shown in Figures 13 and 14, are not monotonic. Notice that although both \{ s_{n}\} and \{ t_{n}\} are bounded sequences, \{ s_{n}\} diverges and \{ t_{n}\} converges.
The sequence \{u_{n}\}=\{n\} shown in Figure 15 is monotonic, but it is not bounded from above. So, \{u_{n}\} is divergent.

So, there are examples of monotonic sequences that diverge and examples of bounded sequences that diverge. However, when a sequence is both monotonic and bounded, it always converges.
IN WORDS
A bounded, monotonic sequence converges.
THEOREM
An increasing (or nondecreasing) sequence \{ s_{n}\} that is bounded from above converges. A decreasing (or nonincreasing) sequence \{ s_{n}\} that is bounded from below converges.
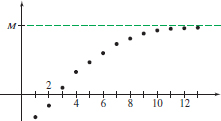
Since the convergence of a sequence \{ s_{n}\} is about the behavior of \{ s_{n}\} for large values of n, if a sequence eventually increases and is bounded from above, it is convergent. Similar remarks hold for sequences that eventually decrease and are bounded from below.
The proof of this theorem can be found in Appendix B. Figure 16 illustrates the theorem for a sequence that is increasing and bounded from above.
EXAMPLE 15Determining if a Sequence Converges or Diverges
Determine if the sequence \{ s_{n}\} =\left\{ {\dfrac{2^{n}}{n!}}\right\} converges or diverges.
Solution To see if \left\{ \dfrac{2^{n}}{n!}\right\} is monotonic, find the algebraic ratio \dfrac{s_{n+1}}{s_{n}}: \frac{s_{n+1}}{s_{n}}=\frac{\dfrac{2^{n+1}}{(n+1)!}}{\dfrac{2^{n}}{n!}}=\frac{2^{n+1}\,n!}{(n+1)!\,2^{n}}=\frac{2}{n+1}\leq 1 \qquad \hbox{ for all }n \geq 1
Since s_{n+1}\leq s_{n} for n\geq 1, the sequence \{ s_{n}\} is nonincreasing.
Next, since each term of the sequence is positive, s_{n}>0 for n\geq 1, the sequence \{ s_{n}\} is bounded from below.
Since \{ s_{n}\} is nonincreasing and bounded from below, it converges.
NOW WORK
NOTE
Although the sequence \{ s_{n}\} converges, the theorem does not tell us what \lim\limits_{n\,\rightarrow \,\infty }s_{n} equals.
550
Summary
To determine whether a sequence converges:
- Look at a few terms of the sequence to see if a trend is developing. For example, the first five terms of the sequence \left\{ 1+\dfrac{(-1)^{n}}{n^{2}}\right\} are 1-1, 1+\dfrac{1}{4}, 1-\dfrac{1}{9}, 1+\dfrac{1}{16}, and 1-\dfrac{1}{25}. The pattern suggests that the sequence converges to 1.
- Find the limit of the nth term using any available limit technique, including basic limits, limit properties, or a related function (possibly using L’Hôpital’s Rule). For example, for the sequence \left\{ \dfrac{\ln n}{n}\right\}, we examine the limit of the related function f(x) =\dfrac{\ln x}{x}. \lim\limits_{x\rightarrow \,\infty }\,f(x)= \lim\limits_{x\,\rightarrow \,\infty }\left( \frac{\ln x}{x}\right) =\lim\limits_{x\,\rightarrow \,\infty }\frac{\dfrac{1}{x}}{1}=0 and conclude the sequence \left\{ \dfrac{\ln n}{n}\right\} converges to 0.
- Show that the sequence is bounded and monotonic.