7.8 Improper IntegralsPrinted Page 523
OBJECTIVES
When you finish this section, you should be able to:
In Chapter 5, the definition of the definite integral ∫baf(x)dx required that both a and b be real numbers. We also required that the function f be defined on the closed interval [a,b]. Here, we take up instances for which:
- Integrals have infinite limits of integration: ∫∞11√xdx∫0−∞x−3x3−8dx∫∞−∞x(x2+1)2dx
- The integrand is not defined at a number in the interval of integration: ∫101√xdx∫π/20tanxdx∫1−11x3dx
Integrals like these are called improper integrals.
524
DEFINITION Improper Integral
If a function f is continuous on the interval [a,∞), then ∫∞af(x)dx, called an improper integral, is defined as \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{a}^{\infty }f(x)~dx=\lim\limits_{b \rightarrow \infty} \int_{a}^{b}f(x)~dx}
provided the limit exists as a real number. If \lim\limits_{b\rightarrow \infty }\int_{a}^{b} f(x)\,dx exists as a real number, the improper integral \int_{a}^{\infty }f(x)\,dx is said to converge. If the limit does not exist or if the limit is infinite, the improper integral \int_{a}^{\infty } f(x)\,dx is said to diverge.
If a function f is continuous on the interval (-\,\infty ,\,b ], then \int_{-\infty }^{b} f(x)\,dx, called an improper integral, is defined as \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{-\infty }^{b}f(x)\,dx=\lim\limits_{\,a\,\rightarrow \,-\infty }\int_{a}^{b} f(x)\,dx }
provided the limit exists as a real number. If \lim\limits_{a\rightarrow -\infty }\int_{a}^{b} f(x)\,dx exists as a real number, the improper integral \int_{-\infty }^{b}f(x)\,dx converges. If the limit does not exist or if the limit is infinite, the improper integral \int_{-\infty }^{b} f(x)\,dx diverges.
1 Find Integrals with an Infinite Limit of IntegrationPrinted Page 524
EXAMPLE 1Integrating Functions over Infinite Intervals
Determine whether the following improper integrals converge or diverge:
- (a) \int_{1}^{\infty }\dfrac{1}{x}\,dx
- (b) \int_{-\infty }^{0}e^{x}\,dx
- (c) \int_{\pi/2}^{\infty }\sin x \,dx
Solution
(a) \int_{1}^{\infty }\dfrac{1}{x}\,dx{:} \lim\limits_{b\,\rightarrow \,\infty }\int_{1}^{b}\dfrac{1}{x} \,dx=\lim\limits_{b\,\rightarrow \,\infty }\big[\ln \,\vert x \vert \big] _{1}^{b}=\lim\limits_{b\,\rightarrow \,\infty }[ \ln b-\ln 1] = \infty.
The limit is infinite, so \int_{1}^{\infty }\dfrac{1}{x}\,dx diverges.
(b) \int_{-\infty }^{0} e^{x}\,dx: \lim\limits_{a\, \rightarrow \,-\infty }\int_{a}^{0}e^{x}\,dx=\lim\limits_{a\,\rightarrow \,-\infty }\big[e^{x}\big]_{a}^{0}=\lim\limits_{a\,\rightarrow \,-\infty }(1-e^{a}) = 1-0=1. Since the limit exists, \int_{-\infty }^{0}e^{x}\,dx converges and equals 1.
(c) \begin{eqnarray*} \int_{\pi/2}^{\infty }\sin x \,dx: \lim\limits_{b\,\rightarrow \,\infty }\int_{\pi/2}^{b}\sin x\, dx &=& \lim\limits_{b\,\rightarrow \,\infty }\,\big[ -\cos x \big]^b_{\pi/2}\\ &=& \lim\limits_{b\,\rightarrow \,\infty } [ - \cos b +0 ] \\ &=& - \lim\limits_{b\,\rightarrow \,\infty }\cos b \end{eqnarray*}
This limit does not exist, since as b\rightarrow \infty, the value of \cos b oscillates between -1 and 1. So, \int_{\pi/2}^{\infty }\sin x \,dx diverges.
NEED TO REVIEW?
Limits at infinity are discussed in Section 1.5, pp. 117-122.
NOW WORK
525
If both limits of integration are infinite, then the following definition is used.
If a function f is continuous for all x and if, for any number c, both improper integrals \int_{-\infty }^{c}f(x)~dx and \int_{c}^{\infty }f(x)~dx converge, then the improper integral \int_{-\infty }^{\infty }f(x)~dx converges, and \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{-\infty }^{\infty }f(x)~dx= \int_{-\infty}^{c}f(x)~dx+ \int_{c}^{\infty } f(x)~dx}
If either or both of the integrals on the right diverge, then the improper integral \int_{-\infty }^{\infty } f(x)\,dx diverges.
EXAMPLE 2Integrating Functions over Infinite Intervals
Determine whether \int_{-\infty }^{\,\infty }4x^{3}\,dx converges or diverges.
Solution We begin by writing \int_{-\infty }^{\,\infty }4x^{3}\,dx=\int_{-\infty }^{\,0}4x^{3}\,dx+\int_{0}^{\,\infty }4x^{3}\,dx and evaluate each improper integral on the right. \int_{-\infty }^{0}4x^{3}\,dx\hbox{:} \quad \lim_{a\,\rightarrow \,-\infty }\left( 4\int_{a}^{0}x^{3}\,dx\right) = \lim_{a\,\rightarrow \,-\infty }\left[ x^{4}\right] _{a}^{0}=\lim_{a\,\rightarrow -\infty }(0-a^{4})=-\infty
There is no need to continue. \int_{-\infty }^{\,\infty }4x^{3}\,dx diverges.
NOTE
The decision to use 0 to break up the integral is arbitrary. Usually, the choice made simplifies finding the integral.
CAUTION The definition requires that two improper integrals converge in order for \int_{-\infty }^{\,\infty} f(x)\,dx to converge. Do not set \int_{-\infty }^{\,\infty }f(x)\,dx=\lim\limits_{a\,\rightarrow \,\infty }\int_{-a}^{a}f(x)\,dx. If this were done in Example 2, the result would have been \int_{-a}^{a}{ 4x}^{3} \,dx=\left[x^{4}\right] _{-a}^{a} =a^{4}-a^{4}=0, and we would have incorrectly concluded that \int_{-\infty }^{\,\infty }f(x)\,dx converges and equals 0.
NOW WORK
2 Interpret an Improper Integral GeometricallyPrinted Page 525
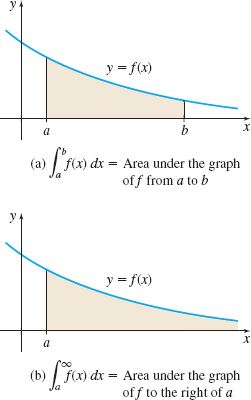
If a function f is continuous and nonnegative on the interval [ a,\,\infty), then \int_{a}^{\infty }f(x)\,dx can be interpreted geometrically. For each number b \gt a, the definite integral \int_{a}^{b} f(x)\,dx represents the area under the graph of y=f(x) from a to b, as shown in Figure 21(a). As b\rightarrow \infty, this area approaches the area under the graph of y=f(x) over the interval [a,\,\infty ), as shown in Figure 21(b). The area under the graph of y=f(x) to the right of a is defined by \int_{a}^{\infty }f(x)\,dx , provided the improper integral converges. If it diverges, there is no area defined.
EXAMPLE 3Determining If the Area Under a Graph Is Defined
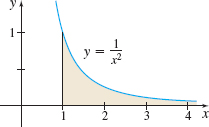
Determine if the area under the graph of y=\frac{1}{x^{2}} to the right of x=1 is defined.
Solution See Figure 22. To determine if the area is defined, we examine \int_{1}^{\infty }\,\frac{1}{x^{2}}dx. \int_{1}^{\infty }\frac{1}{x^{2}}dx\hbox{:}\quad \lim_{b\,\rightarrow \,\infty }\int_{1}^{b}\frac{1}{x^{2}}dx= \lim_{b\,\rightarrow \,\infty } \left[ -\frac{1}{x}\right] _{1}^{b}= \lim_{b\,\rightarrow \,\infty }\left( - \frac{1}{b}+1\right) =1
The area under the graph f(x)= \frac{1}{x^{2}} to the right of 1 is defined and equals 1 square unit.
NOW WORK
526
In Example 1(a), we found that \int_{1}^{\infty }\frac{1}{x}dx diverges, but Example 3 shows \int_{1}^{\infty }\frac{1}{x^{2}}dx converges. Yet, as Figure 23 illustrates, the graphs of y=\frac{1}{x} and y=\frac{1 }{x^{2}} on the interval [1,\infty] are very similar. The difference is that y=\dfrac{1}{x^{2}} approaches 0 more rapidly than y= \frac{1}{x} as x\rightarrow \infty. The next result generalizes these conclusions and is used in Chapter 8.
THEOREM
\int_{1}^{\,\infty }\frac{dx}{x^{p}} converges if p \gt1 and diverges if p \le 1.
Proof
We consider two cases: p=1 and p \ne 1. \begin{eqnarray*} p=1\hbox{;}\quad \int_{1}^{\infty }\frac{dx}{x^{p}}=\int_{1}^{\infty }\frac{dx}{x}\hbox{:}\quad \lim\limits_{b\rightarrow \infty }\int_{1}^{b}\frac{dx}{x}=\lim\limits_{b\rightarrow \infty }\ln b=\infty \end{eqnarray*} From Example 1(a) \begin{eqnarray*} p \ne 1\hbox{;}\quad \int_{1}^{\infty }\frac{dx}{x^{p}}\hbox{:}\quad \lim\limits_{b\rightarrow \infty }\int_{1}^{b}\frac{dx}{x^{p}} &=&\lim\limits_{b\rightarrow \infty }\left[ \frac{x^{-p+1}}{-p+1}\right] _{1}^{b}\\ &=&\lim\limits_{b\rightarrow \infty }\left[\frac{1}{1-p}( b^{-p+1}-1) \right] \\ &=&\dfrac{1}{1-p}\lim\limits_{b\rightarrow \infty }\left( \frac{1}{b^{p-1}}-1\right) \end{eqnarray*}
If p \gt1, then p-1 \gt0, and \lim\limits_{b\,\rightarrow \,\infty }\dfrac{1}{b^{p-1}}=0. So, \int_{1}^{\infty }\frac{dx}{x^{p}}=\frac{1}{1-p}( 0-1) =\frac{1 }{p-1}
and the improper integral \int_{1}^{\infty }\frac{dx}{x^{p}}, p>1, converges.
If p \lt1, then p-1 \lt0, and \lim\limits_{b\,\rightarrow \,\infty }\dfrac{1}{ b^{p-1}}=\lim\limits_{b\,\rightarrow \,\infty }b^{1-p}=\infty. So, the improper integral \int_{1}^{\infty }\dfrac{dx}{x^{p}}, p \lt1, diverges.
NOTE Interesting Fact
The area under the graph of y=\dfrac{1}{x} to the right of 1 is not defined [see Example 1(a)], but the volume obtained by revolving the region with this same area about the x-axis is defined.
EXAMPLE 4Finding the Volume of Gabriel’s Horn
Find the volume of the solid of revolution, called Gabriel’s Horn, that is generated by revolving the region bounded by the graph of y=\frac{1}{x} and the x-axis to the right of 1 about the x-axis. Use the disk method.
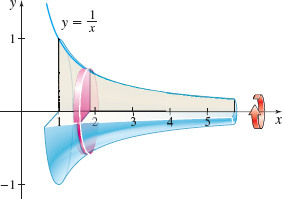
Solution Figure 24 illustrates the region being revolved and the solid of revolution that it generates. Using the disk method, the volume V is \begin{eqnarray*} V=\pi \int_{1}^{\infty }\!\!\left( \frac{1}{x}\right) ^{2} dx\hbox{:}\quad \pi \lim\limits_{b\,\rightarrow \,\infty }\int_{1}^{b}\!\!\frac{1}{x^{2}} \,dx&=&\pi \lim\limits_{b\rightarrow \infty }\left[ -\frac{1}{x}\right] _{1}^{b}\\[6pt] &=&\pi \lim\limits_{b\rightarrow \,\infty }\left( -\frac{1}{b} + 1\right) = \pi \end{eqnarray*}
The volume of the solid of revolution is \pi cubic units.
NOW WORK
3 Integrate Functions over [a,b] That Are Not Defined EndpointPrinted Page 527
527
IN WORDS
These improper integrals, sometimes called improper integrals of the second kind, have finite limits of integration, but the integrand is not defined at one (but not both) of them.
DEFINITION
If a function f is continuous on (a, b], but is not defined at a, then \int_{a}^{b}\!f(x)\,dx is an improper integral, and \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{a}^{b} f(x)\,dx=\lim\limits_{t\,\rightarrow \,a^{+}} \int_{t}^{b} f(x)\,dx }
provided the limit exists as a real number.
If a function f is continuous on [a,b), but is not defined at b, then \int_{a}^{b} f(x)\,dx is an improper integral, and \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{a}^{b} f(x)\,dx=\lim\limits_{t\,\rightarrow \,b^{-}} \int_{a}^{t} f(x)\,dx }
provided the limit exists as a real number.
When the limit exists as a real number, the improper integral is said to converge; otherwise, it is said to diverge.
Be sure to use the correct one-sided limit. If f is not defined at the left endpoint a, then for t to be in the interval of integration, t \gt a and t must approach a from the right. Similarly, if f is not defined at the right endpoint b, then for t to be in the interval of integration, t\lt b and t must approach b from the left. Figure 25 may help you remember the correct one-sided limit to use.
If a function f is continuous and nonnegative on the interval (a,b], then the improper integral \int_{a}^{b} f(x)\,dx may be interpreted geometrically. For each number t, a \lt t \le b, the integral \int_{t}^{b}f(x)\,dx represents the area under the graph of y = f(x) from t to b, as shown in Figure 26(a). As t\rightarrow a^{+}, this area approaches the area under the graph of y = f(x) from a to b, as shown in Figure 26(b). That is, if \int_{a}^{b} f(x)\,dx converges, its value is defined to be the area A under the graph of f from a to b.
EXAMPLE 5Determining If the Area Under a Graph Is Defined
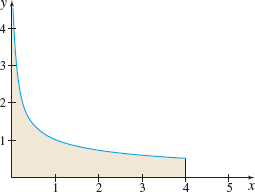
Determine if the area under the graph of y=\dfrac{1}{\sqrt{x}} from 0 to 4 is defined.
Solution Figure 27 shows the area under the graph of y=\dfrac{1}{ \sqrt{x}} from 0 to 4. The area is given by \int_{0}^{4}\dfrac{1}{ \sqrt{x}}dx. Since the integrand f(x)=\dfrac{1}{\sqrt{x}} is continuous on (0, 4] but is not defined at 0, \int_{0}^{4}\dfrac{1}{ \sqrt{x}}~dx is an improper integral. \begin{eqnarray*} \int_{0}^{4}\dfrac{1}{\sqrt{x}}\,dx:\quad \lim_{t\,\rightarrow \,0^{+}}\int_{t}^{4}\dfrac{1}{\sqrt{x}}\,dx &=& \lim_{t\,\rightarrow \,0^{+}}\int_{t}^{4}x^{-1/2}dx=\lim_{t\,\rightarrow \,0^{{ +} }}\left[ \dfrac{x^{1/2}}{\dfrac{1}{2}}\right] _{t}^{4}\\[5pt] &=& \lim_{t\,\rightarrow \,0^{+}}\big( 2\cdot 2-2\sqrt{t}\,\big) =4-2\lim_{t\,\rightarrow \,0^{+}}\sqrt{t}=4 \end{eqnarray*} So, \int_{0}^{4}\dfrac{1}{\sqrt{ x}}\,dx converges, and the area under the graph of y=\dfrac{1}{\sqrt{x}} from 0 to 4 is defined and equals 4.
NOW WORK
528
EXAMPLE 6Determining Whether an Improper Integral Converges or Diverges
Determine whether \int_{0}^{\pi /2}\tan x\,dx converges or diverges.
Solution The function f (x) = \tan x is continuous on \left[ 0,\,\dfrac{\pi }{2}\right) but is not defined at \dfrac{\pi }{2}, so \int_{0}^{\pi /2}\tan x\,dx is an improper integral. \begin{eqnarray*} \int_{0}^{\pi /2}\tan x~dx\hbox{:} \lim\limits_{t\,\rightarrow \left( \pi /2\right) ^{-}}\int_{0}^{t}\tan x\,dx&=&\lim\limits_{t\,\rightarrow \ (\pi /2) ^{-}}\big[ \ln \vert \sec x \vert\big] _{0}^{t}\\[4pt] &=&\lim\limits_{t\,\rightarrow (\pi /2) ^{-}}[\ln \vert \sec t \vert -\ln \vert \sec 0 \vert ] \\[4pt] &=& \lim\limits_{t\,\rightarrow (\pi /2) ^{-}}\ln (\sec t)=\infty \end{eqnarray*}
So, \int_{0}^{\pi /2}\tan x\,dx diverges.
NOW WORK
Another type of improper integral occurs when the integrand is not defined at some number c, a<c<b, in the interval [a,b].
DEFINITION
If a function f is continuous on a closed interval [a,b], except at the number c, a<c<b, where f is not defined, the integral \int_{a}^{b} f(x)\,dx is an improper integral and \bbox[5px, border:1px solid black, #F9F7ED]{ \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx+ \int_{c}^{b}f (x)\,dx }
provided that both improper integrals on the right converge.
If either improper integral \int_{a}^{c}f(x)\,dx or \int_{c}^{b}f(x) \,dx diverges, then the improper integral \int_{a}^{b}f(x)\,dx also diverges.
EXAMPLE 7Determining Whether an Improper Integral Converges or Diverges
Determine whether \int_{0}^{2}\dfrac{1}{(x-1)^{2}}\,dx converges or diverges.
Solution Since f(x)=\dfrac{1}{(x-1) ^{2}} is not defined at 1, the integral \int_{0}^{2}\dfrac{1}{(x-1)^{2}}\,dx is an improper integral on the interval [ 0, 2]. We write the integral as follows: \int_{0}^{2}\dfrac{1}{(x-1)^{2}}\,dx=\int_{0}^{1}\dfrac{1}{(x-1)^{2}} \,dx+\int_{1}^{2}\dfrac{1}{(x-1)^{2}}\,dx
and investigate each of the two improper integrals on the right. \int_{0}^{1}\!\!\dfrac{1}{(x-1)^{2}}\,dx:\quad \lim_{t\,\rightarrow \,1^{-}}\int_{0}^{t}\dfrac{1}{(x-1)^{2}}\,dx=\lim_{t\rightarrow 1^{-}}\left[ \dfrac{-1}{x-1}\right] _{0}^{t}\!=\lim_{t\rightarrow 1^{-}}\left( \dfrac{-1}{t-1} -1\!\right)\! =\infty \int_{0}^{1}\dfrac{1}{(x-1) ^{2}}\,dx diverges, so there is no need to investigate the second integral.
The improper integral \int_{0}^{2}\dfrac{1}{(x-1) ^{2}}\,dx diverges.
CAUTION
It is a common mistake to look at an improper integral like \int_{0}^{2}\dfrac{dx}{(x-1) ^{2}} and not notice that the integrand is undefined at 1. If that happens, and you use the Fundamental Theorem of Calculus, you obtain \int_{0}^{2}\dfrac{dx}{(x-1)^{2}}=\left[ \dfrac{-1}{x-1}\right] _{0}^{2}=-1-1=-2 which is an incorrect answer. Always check the domain of the integrand before attempting to integrate.
NOW WORK
4 Use the Comparison Test for Improper IntegralsPrinted Page 529
529
So far we have been able to determine whether an improper integral converges or diverges by finding an antiderivative of the integrand. If we cannot find an antiderivative, we may still be able to determine whether the improper integral converges or diverges. Then, if it converges, we can use numerical techniques such as the Trapezoidal Rule or Simpson’s Rule to approximate the integral. One way to determine if an improper integral converges or diverges is by using the Comparison Test for Improper Integrals.
THEOREM Comparison Test for Improper Integrals
Let f and g be two functions that are nonnegative and continuous on the interval \left[ a,\infty \right) , and suppose f( x) \ge g( x)
for all numbers x>c, where c \ge a.
- If \int_{a}^{\infty}f(x)\,dx converges, then \int_{a}^{\infty }g(x)\,dx also converges
- If \int_{a}^{\infty }g(x)\,dx diverges, then \int_{a}^{\infty}f(x)\,dx also diverges.
You are asked to prove the theorem in Problem 96. The proof follows from a property of definite integrals: If the functions f and g are continuous on a closed interval [a,b] and if f(x) \ge \,g(x) on [a,b], then \int_{a}^{b}f(x)\,dx \ge \int_{a}^{b}g(x)\,dx. (See Section 5.4, Problem 114, p. 378.)
EXAMPLE 8Using the Comparison Test for Improper Integrals
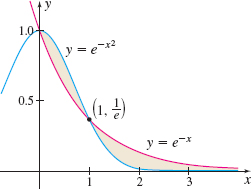
Determine whether \int_{1}^{\infty }e^{-x^{2}}dx converges or diverges.
Solution By definition, \int_{1}^{\infty }e^{-x^{2}}dx=\lim\limits_{b\rightarrow \infty }\int_{1}^{b}e^{-x^{2}}dx converges if the limit exists and equals a real number. Since e^{-x^{2}} has no antiderivative, we use the Comparison Test for Improper Integrals. We proceed as follows: For x \ge 1, \begin{eqnarray*} \begin{array}{rcl@{\qquad}l} x^{2} &\geq & x \\[3pt] -x^{2} &\leq & -x \\[3pt] 0 &\lt&e^{-x^{2}}\leq e^{-x} & {\color{#0066A7}{\hbox{ Since }{e>1}\hbox{, if }{a\leq b}\hbox{, then }{e}^{a}{\leq e}^{b}.}} \end{array} \end{eqnarray*}
Figure 28 illustrates this.
Based on the Comparison Test, if \int_{1}^{\infty }e^{-x}dx converges, so does \int_{1}^{\infty }e^{-x^{2}}dx. We investigate \int_{1}^{\infty }e^{-x}dx. \begin{eqnarray*} \int_{1}^{\infty }e^{-x}dx :\quad\!\!\!\! \lim\limits_{b\rightarrow \infty }\int_{1}^{b}e^{-x}dx &=& \lim\limits_{b\rightarrow \infty }\!\big[-e^{-x}\big] _{1}^{b}=\lim\limits_{b\rightarrow \infty }[-e^{-b}+e^{-1}] =\lim\limits_{b\rightarrow \infty }\left[ \dfrac{1}{e}-\dfrac{1}{e^{b}} \!\right] \\[5pt] &=& \lim\limits_{b\rightarrow \infty }\dfrac{1}{e}-\lim\limits_{b \rightarrow \infty }\dfrac{1}{e^{b}}=\dfrac{1}{e} \end{eqnarray*}
Since \int_{1}^{\infty }e^{-x}dx converges, we conclude that \int_{1}^{\infty}e^{-x^{2}}dx converges.
Notice that the Comparison Test for Improper Integrals does not give the value of \int_{1}^{\infty }e^{-x^{2}}dx. To find \int_{1}^{\infty }e^{-x^{2}}dx requires numerical techniques. The Comparison Test does, however, tell us that 0 \le \int_{1}^{\infty}e^{-x^{2}}dx \le \dfrac{1}{e}.