1. Multiple Choice If the series $\sum\limits_{k\,=\,1}^{ \infty }a_{k}$, $a_{k}>0$, converges then $\lim\limits_{n\,\rightarrow \,\infty }a_{n}=$ [(a) $0$, (b) $a_{1}$, (c) $a_{n}$, (d) $\infty$].

2. True or False If $\lim\limits_{n\rightarrow \infty }a_{n}=0,$ then the series $\sum\limits_{k\,=\,1}^{\infty }a_{k}$ converges.

3. True or False The series $\sum\limits_{k=1}^{\infty}\,k^{3}$ diverges.

4. True or False If the first 100 terms of two infinite series are different, but from the 101st term on they are identical, then either both series converge or both series diverge.

5. True or False If $\sum\limits_{k\,=\,1}^{\infty }(a_{k}+b_{k})$ converges, then $\sum\limits_{k\,=\,1}^{\infty }a_{k}$ converges and $\sum\limits_{k\,=\,1}^{\infty }b_{k}$ converges.

6. True or False If $\sum\limits_{k\,=\,1}^{\infty }a_{k}=S$ is a convergent series and $c$ is a nonzero real number, then $\sum\limits_{k\,=\,1}^{\infty }(ca_{k})=cS.$

7. True or False Let $f$ be a function defined on the interval $[1,\infty)$ that is continuous, positive, and decreasing on its domain. Let $a_{k}=f(k)$ for all positive integers $k$. Then the series $\sum\limits_{k\,=\,1}^{\infty }a_{k}$ converges if and only if the improper integral $\int_{1}^{\infty}f(x)\,dx$ converges.

8. True or False For an infinite series of positive terms, if its sequence of partial sums is not bounded, then you cannot tell if the series converges or diverges.

9. The $p$-series $\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}$ converges if ______________ and diverges if ______________.

10. Does $\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{3/2}}$ converge or diverge?

11. Does $\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{-1/2}}$ converge or diverge?

12. True or False If $p>1$, then the convergent $p$-series $\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}$ is bounded by $\dfrac{1}{p-1}<\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k^{p}}<1$.

13. $\sum\limits_{k=1}^{\infty }16$

14. $\sum\limits_{k=1}^{\infty }\dfrac{k+9}{k}$

15. $\sum\limits_{k=1}^{\infty }\ln k$

16. $\sum\limits_{k=1}^{\infty }e^{k}$

17. $\sum\limits_{k=1}^{\infty }\dfrac{k^{2}}{k^{2}+4}$

18. $\sum\limits_{k=1}^{\infty}\dfrac{k^{2}+3}{\sqrt{k}}$

19. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{1.01}}$

20. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{0.9}}$

21. $\sum\limits_{k=1}^{\infty }\dfrac{\ln k}{k}$

22. $\sum\limits_{k=2}^{\infty }\dfrac{1}{k\sqrt{\ln k}}$

23. $\sum\limits_{k=1}^{\infty }ke^{-k^{2}}$

24. $\sum\limits_{k=1}^{\infty }ke^{-k}$

25. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{2}+1}$

26. $\sum\limits_{k=2}^{\infty }\dfrac{1}{k\sqrt{k^{2}-1}}$

27. $\sum\limits_{k=2}^{\infty }\dfrac{1}{k\ln k}$

28. $\sum\limits_{k=2}^{\infty }\dfrac{1}{k(\ln k)^{3}}$

29. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{2}}$

30. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{4}}$

31. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{1/3}}$

32. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{2/3}}$

33. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{e}}$

34. $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{\pi }}$

35. $1+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{3\sqrt{3}}+\dfrac{1}{4\sqrt{4}}+\cdots$

574

36. $1+\dfrac{1}{\sqrt[3]{2}}+\dfrac{1}{\sqrt[3]{3}}+\dfrac{1}{\sqrt[3]{4}}+\cdots$

37. $1+\dfrac{1}{4\sqrt{2}}+\dfrac{1}{9\sqrt{3}}+\dfrac{1}{16\sqrt{4}}+\cdots$

38. $1+\dfrac{1}{8}+\dfrac{1}{27}+\dfrac{1}{64}+\cdots$

39. $\sum\limits_{k=1}^{\infty }\dfrac{10}{k}$

40. $\sum\limits_{k=1}^{\infty}\dfrac{2}{1+k}$

41. $\sum\limits_{k=1}^{\infty}\dfrac{k^{2}+1}{4k+1}$

42. $\sum\limits_{k=1}^{\infty}\dfrac{k^{3}}{k^{3}+3}$

43. $\sum\limits_{k=1}^{\infty} \, \left(k+\dfrac{1}{k}\right)$

44. $\sum\limits_{k=1}^{\infty} \, \left(\dfrac{1}{3^{k}}-\dfrac{1}{4^{k}}\right)$

45. $\sum\limits_{k=1}^{\infty} \, \left(\dfrac{1}{3k}-\dfrac{1}{4k}\right)$

46. $\sum\limits_{k=1}^{\infty} \, \left(k-\dfrac{10}{k}\right)$

47. $\sum\limits_{k=1}^{\infty}\sin \, \left(\dfrac{\pi }{2}k\right)$

48. $\sum\limits_{k=1}^{\infty}\sec (\pi k)$

49. $\sum\limits_{k=3}^{\infty}\dfrac{k+1}{k-2}$

50. $\sum\limits_{k=5}^{\infty}\dfrac{2k^{5}+3}{k^{5}-4k^{4}}$

51. $\sum\limits_{k=2}^{\infty}\dfrac{1}{k(\ln k)^{1/2}}$

52. $\sum\limits_{k=2}^{\infty}\dfrac{1}{k(\ln k)^{2}}$

53. $\sum\limits_{k=3}^{\infty}\dfrac{2k}{k^{2}-4}$

54. $\sum\limits_{k=1}^{\infty}\dfrac{1}{(2k-1) (2k)}$

55. Integral Test Use the Integral Test to show that the series $\sum\limits_{k\,=2}^{\infty }\dfrac{1}{k(\ln k)^{p}}$, $p > 0$ converges if and only if $p>1$.

56. Integral Test Use the Integral Test to show that the series $\sum\limits_{k\,=3}^{\infty }\dfrac{1}{k(\ln k)\left[ \ln (\ln k)^{p}\right] }$ converges if and only if $p>1$.

57. Faulty Logic Let $S=1+2+4+8+\cdots .$ Then $$2S=2+4+8+16+\cdots =-1+(1+2+4+\cdots )=-1+S$$

    Therefore, $$S=1+2+4+8+\cdots =-1$$

    What went wrong here?

58. Find examples to show that the series $\sum\limits_{k\,=1}^{ \infty }(a_{k}+b_{k})$ and $\sum\limits_{k\,=1}^{\infty }(a_{k}-b_{k})$ may converge or diverge if $\sum\limits_{k\,=1}^{\infty }a_{k}$ and $\sum\limits_{k\,=1}^{\infty }b_{k}$ each diverge.

59. Approximating $\pi^{2}$ The $p$-series $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{2}}$ converges.

    1. (a) Find the sum of the series in exact form.
    2. (b) Use the first hundred terms of the series to approximate $\pi ^{2}.$

60. The $p$-series $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{3}}$ converges.

    1. (a) Provide an interval of width 1 that contains the sum $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{3}}.$
    2. (b) Use the first hundred terms of the series to approximate the sum.

61. $\sum\limits_{k=1}^{\infty} \, \left( k^{6}e^{-k}\right)$

62. $\sum\limits_{k=1}^{\infty}\dfrac{k+3}{k^{2}+6k+7}$

63. $\sum\limits_{k=2}^{\infty}\dfrac{5k+6}{k^{3}-1}$

64. The $p$-series $\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{p}}$ converges for $p>1$ and diverges for $0<p\leq 1$. The series $\sum\limits_{k=1}^{\infty }a_{k}=\sum\limits_{k=1}^{\infty }\dfrac{1}{ k^{0.99}}$ diverges and the series $\sum\limits_{k=1}^{\infty }b_{k}=\sum\limits_{k=1}^{\infty }\dfrac{1}{k^{1.01}}$ converges.

    1. (a) Find the partial sums $S_{10},$ $S_{1000}$, and $S_{100,000}$ for each series.
    2. (b) Explain the results found in (a).

65. Show that the sum of two convergent series is a convergent series.

66. Show that for a nonzero real number $c$, if $\sum\limits_{k\,=1}^{\infty }a_{k}=S$ is a convergent series, then the series $\sum\limits_{k\,=1}^{\infty }(ca_{k})=cS$.

67. Suppose $\sum\limits_{k\,=N+1}^{\infty }a_{k}=S$ and $a_{1}+a_{2}+\cdots +a_{N}=K$. Prove that $\sum\limits_{k\,=1}^{\infty }a_{k}$ converges and its sum is $S+K$.

68. If $\sum\limits_{k\,=1}^{\infty }a_{k}$ converges and $\sum\limits_{k\,=1}^{\infty }b_{k}$ diverges, then prove that $\sum\limits_{k\,=1}^{\infty }(a_{k}+b_{k})$ diverges.

69. Suppose $\sum\limits_{k=1}^{\infty }a_{k}$ converges, and $a_{n}>0$ for all $n$. Show that $\sum\limits_{k=1}^{\infty }\dfrac{a_{k}}{ 1+a_{k}}$ converges.

70. Determine whether the series $\sum\limits_{k=1}^{\infty}\dfrac{1}{k \ln \, \left( 1+\dfrac{1}{k}\right) }$ converges.

71. Integral Test Use the Integral Test to show that the series $\sum\limits_{k=2}^{\infty }\dfrac{1}{(\ln k) ^{p}}$ diverges for all numbers $p.$

72. For what positive integers $p$ and $q$ does the series $\sum\limits_{k=2}^{\infty }\dfrac{(\ln k) ^{q}}{k^{p}}$ converge?

73. Find all real numbers $x$ for which $\sum\limits_{k\,=\,1}^{\infty }k^{x}$ converges. Express your answer using interval notation.

575

74. Consider the finite sum $S_{n}=\sum\limits_{k\,=\,1}^{n}\dfrac{1}{1+k^{2}}$.

    1. (a) By comparing $S_{n}$ with an appropriate integral, show that $S_{n}\leq \tan ^{-1}n$ for $n\geq 1$.
    2. (b) Use (a) to deduce that $\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{1+k^{2}}$ converges.
    3. (c) Prove that $\dfrac{\pi }{4}\leq \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{1+k^{2}}\leq \dfrac{\pi }{2}$.

75. Riemann’s zeta function is defined as $$\zeta (s)=1+\frac{1}{2^{s}}+\frac{1}{3^{s}}+\cdots \qquad \hbox{for }s>1$$

    As mentioned on page 572, Euler showed that $\zeta (2)=\dfrac{\pi ^{2}}{6}$. He also found the value of the zeta function for many other even values of $s$. As of now, no one knows the value of the zeta function for odd values of $s$. However, it is not too difficult to approximate these values, as this problem demonstrates.

    1. (a) Find $\sum\limits_{k=1}^{10}\dfrac{1}{k^{3}}$.
    2. (b) Using integrals in a way analogous to their use in the proof of the Integral Test, find upper and lower bounds for $\sum\limits_{k\,=\,1}^{\infty}\dfrac{1}{k^{3}}$.
    3. (c) What can you conclude about $\zeta (3)$?

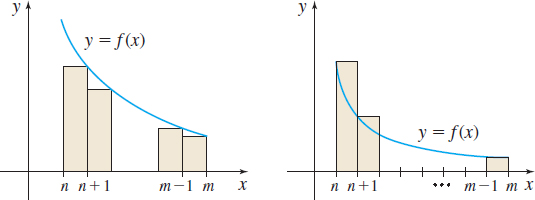
76. 1. (a) By considering graphs like those shown below, show that if $f$ is decreasing, positive, and continuous, then $f(n+1)+\cdots +f(m)\leq \int_{n}^{m} f(x)\,dx\leq f(n)+\cdots +f(m-1)$
    2. (b) Under the assumption of (a), prove that if $\sum\limits_{k\,=\,1}^{\infty}f(k)$ converges, then $$\sum_{k=n+1}^{\infty }f(k)\leq \int_{n}^{\infty} f(x)dx\leq \sum_{k=n}^{\infty }f(k)$$
    3. (c) Let $f(x)=\dfrac{1}{x^{2}}$. Use the inequality in (b) to determine exactly how many terms of the series $\sum\limits_{k\,= \,1}^{\infty }\dfrac{1}{k^{2}}$ one must take in order to have $\vert \hbox{ Error }\vert \, <\left( \dfrac{1}{2}\right) \, 10^{-2}$. How many terms must one take to have $\vert \hbox { Error }\vert \, < \left( \dfrac{1}{2}\right) \, 10^{-10}$?

    Source: Based on an article by R. P. Boas, Jr., American Mathematical Monthly, “Partial Sums of Infinite Series, and How They Grow” Vol. 84, No. 4 (April 1977), pp. 237–258.