
2.5 pH Is an Important Parameter of Biochemical Systems
✓ 6 Define pH and explain why changes in pH may affect biochemical systems.
DID YOU KNOW?
A common example of a pathological modification of environmental pH is gastroesophageal reflux disease, or GERD. A chronic digestive disease, GERD develops when stomach acid refluxes into the esophagus. The backwash of acid, frequently experienced as heartburn, irritates the lining of the esophagus by exposing the tissue to very acidic conditions (pH 1 to 2). GERD can cause chronic inflammation in the esophagus that can lead to complications, including esophageal ulcers and esophageal cancer. Risk factors for GERD include smoking and obesity.
Especially important examples of reversible reactions are those that include the release or binding of a hydrogen ion, H+, also called a proton. The pH of a solution is a measure of the hydrogen ion concentration, with values ranging from 0 to 14. The smaller numbers denote an acidic environment, and the larger numbers denote a basic environment. Indeed, pH is an important parameter of living systems. For example, the pH of human blood is about 7.4, and a deviation of +/−0.5 units can result in coma or death. Why is maintaining the proper pH so vital? Alterations in pH can drastically affect the internal electrostatic environment of an organism, which can alter the weak bonds that maintain the structure of biomolecules. Altered structure usually means loss of function. For instance, ionic bonds may be weakened or disappear with a change in pH, and hydrogen bonds may or may not form, depending on the pH. Given how crucial maintaining proper pH is to the correct functioning of biochemical systems, it is important to have means of describing pH. We will now investigate the quantitative nature of pH, the effect of acids and bases on pH, and the means by which cells maintain an approximately constant pH.
Water Ionizes to a Small Extent
DID YOU KNOW?
In chemistry, equilibrium is the condition in which the concentrations of reactants and products have no net change over time.
Very small amounts of pure water dissociate and form hydronium (H3O+) and hydroxyl (OH−) ions, with the concentration ion of each being 10−7 M. For simplicity, we refer to the hydronium ion simply as a hydrogen ion (H+) and write the equilibrium as
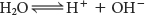
The equilibrium constant Keq of this dissociation is given by
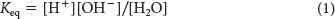
in which the brackets denote molar concentrations (M) of the molecules. Substituting the concentration of H+ and OH− (10−7 M, each) and the concentration of water (55.5 M), we see that the equilibrium constant of water is
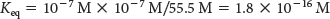
Because the concentration of water is essentially unchanged by the small amount of ionization, we can ignore any change in the concentration of water and define a new constant:
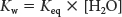
which then simplifies to

Kw is the ion product of water. At 25°C, Kw is 1.0 × 10−14 M2. The pH of any solution is quantitatively defined as
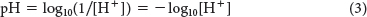
Consequently, the pH of pure water, which contains equal amounts of H+ and OH−, is equal to 7. Note that the concentrations of H+ and OH− are reciprocally related; thus, pH + pOH = 14, where pOH is determined by substituting the hydroxide ion concentration for the proton concentration in equation 3. If the concentration of H+ is high, then the concentration of OH− must be low, and vice versa. For example, if [H+]=10−2 M, then [OH−] = 10−12 M.
Let us consider a problem that is a bit more complex. If the [H+] equals 2.5 × 10−4 M in a solution, what would the [OH−] be? We solve this problem by first remembering the equation for the ion product of water:
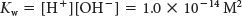
We can determine the [OH–] by rearranging the equation to solve for [OH–] and inserting the proton concentration:
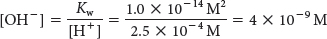
Thus, if the concentration of protons or hydroxyl ions is known, the concentration of the unknown ion can be determined.
An Acid Is a Proton Donor, Whereas a Base Is a Proton Acceptor
Organic acids are prominent biomolecules. These acids will ionize to produce a proton and a base:
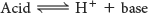
The species formed by the ionization of an acid is its conjugate base and is distinguished from the ionized acid by having the suffix “ate.” Conversely, the protonation of a base yields its conjugate acid. Let’s consider acetic acid, a carboxylic acid. Carboxylic acids are key functional groups found in a host of biochemicals (Table 2.1). Acetic acid and acetate ion are a conjugate acid–

Acids Have Differing Tendencies to Ionize
How can we measure the strength of an acid? For instance, how can we determine whether an acid will dissociate in a given biochemical environment, such as the blood? Let us examine weak acids, inasmuch as weak acids are the type found in biochemical systems. The ionization equilibrium of a weak acid (HA) is given by
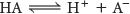
The equilibrium constant Ka for this ionization is

The larger the value of Ka is, the stronger the acid (Figure 2.11).
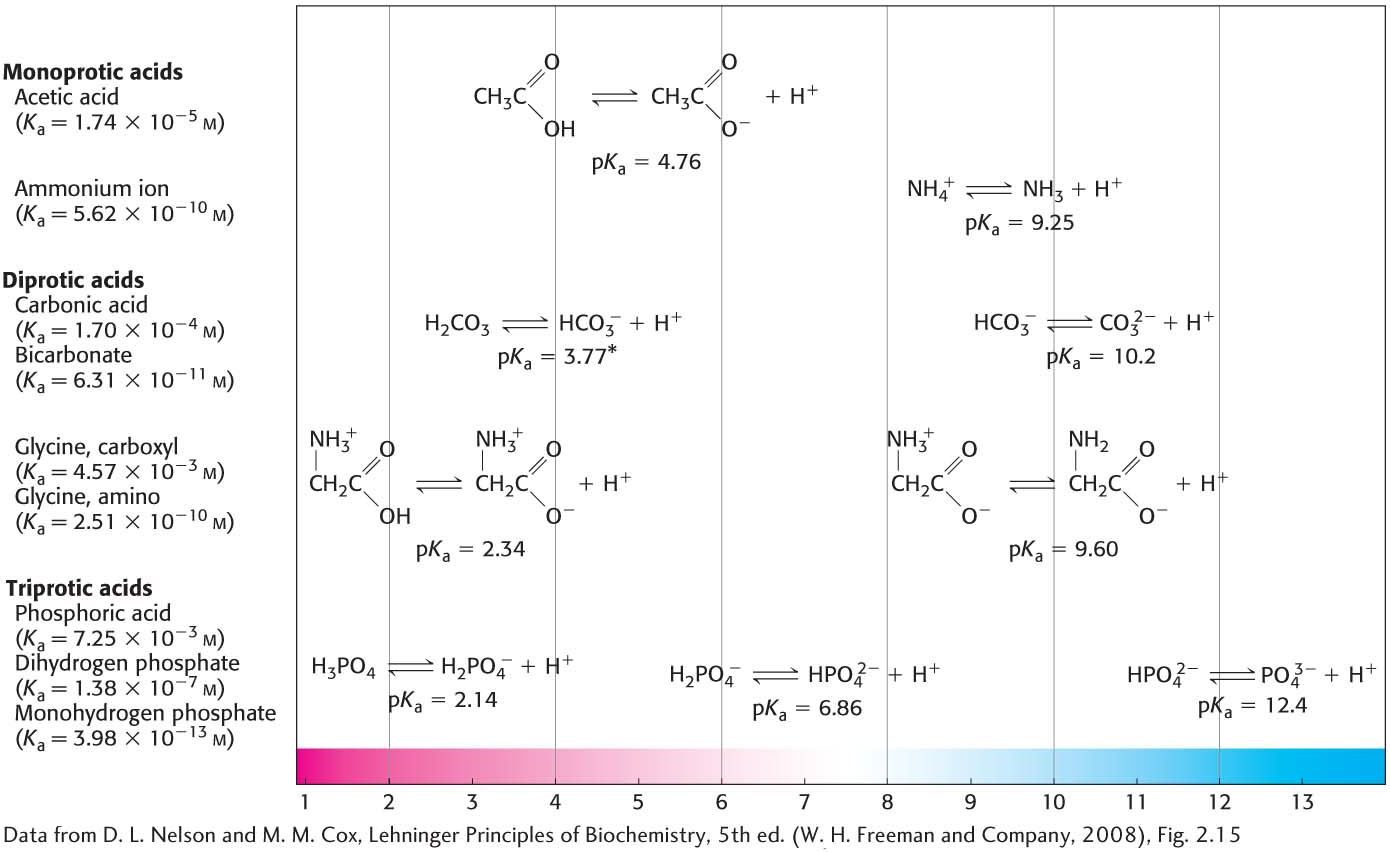
What is the relation between pH and the ratio of acid to base? In other words, how dissociated will an acid be at a particular pH? A useful expression establishing the relation between pH and the acid/base ratio can be obtained by rearrangement of equation 4:

Taking the logarithm of both sides of equation 5 gives
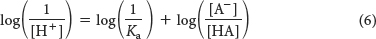
We define log(1/Ka) as the pKa of the acid.
Substituting pH for log 1/[H+] and pKa for log 1/Ka in equation 6 yields

which is commonly known as the Henderson–
Above pKa, [A−] predominates, whereas below pKa, [HA] predominates. As a reference to the strength of an acid, pKa is more useful than the ionization constant (Ka) because pKa does not require the use of the sometimes cumbersome scientific notation. Note from Figure 2.11 that the most important biochemical acids will be predominately dissociated at physiological pH (∼7.4) Thus, these molecules are usually referred to as the conjugate base (e.g., pyruvate) and not as the acid (e.g., pyruvic acid).
Buffers Resist Changes in pH
An acid–

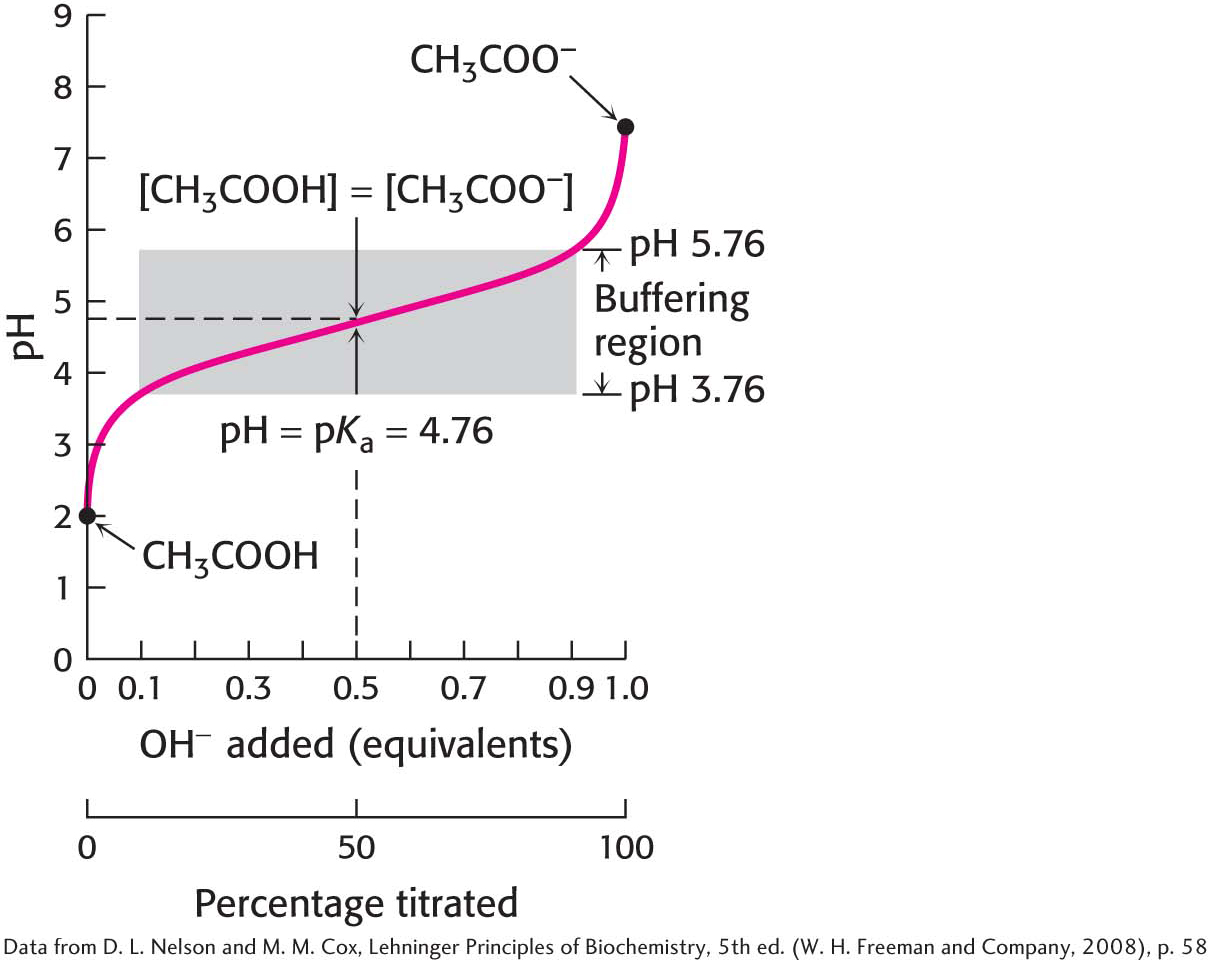
A plot of how the pH of this solution changes with the amount of OH− added is called a titration curve (Figure 2.12). Note that there is an inflection point in the curve at pH 4.8, which is the pKa of acetic acid. In the vicinity of this pH, the addition of a relatively large amount of OH− to the buffer produces little change in the pH of the solution. In other words, the buffer maintains the value of pH near the pKa of the acid component of the buffer, despite the addition of either protons or hydroxide ions. Figure 2.13 compares the changes in pH when a strong acid is added to pure water with the changes in pH when that same strong acid is added to a buffered solution. The pH of the buffered solution does not change nearly as rapidly as that of pure water. In general, a weak acid is most effective in buffering against pH changes in the vicinity of its pKa value. Figure 2.14 shows the buffering range of three different weak acids.

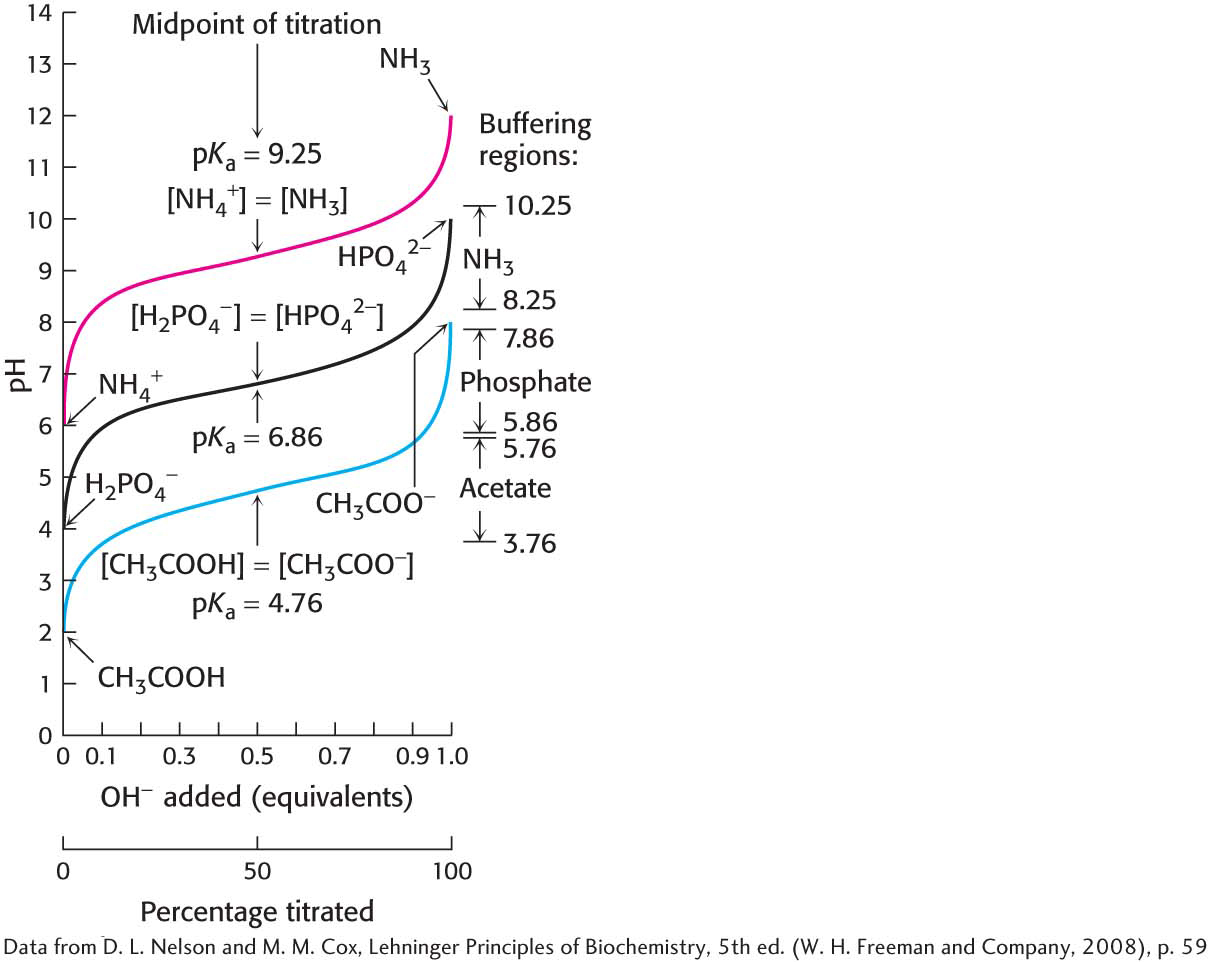
Buffers Are Crucial in Biological Systems
Knowledge of the workings of buffers is important for two reasons. First, much of biochemistry is experimentally investigated in vitro (in glass, or, in effect, in a test tube). Because the biomolecules that are being investigated are sensitive to pH, biochemists must use buffers to maintain the proper pH during the experiments. Choice of the proper buffer is often crucial to designing a successful experiment.
Second, we need to understand buffers so as to understand how an organism controls the pH of its internal environment in vivo—
We will examine the buffering of blood pH as an example of a physiological system. In the aerobic biochemical consumption of fuels, carbon dioxide (CO2) is produced (Chapter 19). The carbon dioxide reacts with water to produce a weak acid, carbonic acid:
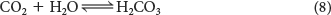
The carbonic acid readily dissociates into a proton and bicarbonate ion:
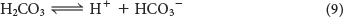
The conjugate acid–
Making Buffers Is a Common Laboratory Practice
Let’s consider an exercise that is common in biological laboratories: making a buffer. Imagine that we have a protein and want to see how the activity changes as a function of pH. To do so, we need buffers covering a range of pH values, and we examine the protein’s activity at each value. As an example, let’s examine how to make 1 liter of 0.3 M acetate buffer, pH 4.46. We have on hand a 2 M solution of acetic acid (a weak acid, pKa = 4.76) and a 2.5 M solution of potassium hydroxide (KOH; a strong base). These solutions are referred to as stock solutions. Remember that an acetate buffer will consist of a mixture of acetate ion and acetic acid; so we must first determine the ratio of acetate to acetic acid that will yield pH 4.46 and then calculate the amount of each constituent needed to yield a total molarity (concentration of acid plus concentration of base) equal to 0.3 M.
Essentially, all buffer problems can be solved with a little introductory chemistry and the Henderson–
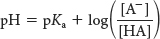
Insert the given parameters:
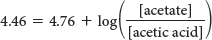
or

Finding the antilog of 0.3 yields
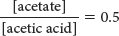
This equation tells us that, to obtain pH = 4.46 with an acetate buffer, two-
First of all, we do not have any acetate solution; we only have acetic acid and potassium hydroxide. Therefore, all of the acetate in the buffer will come from acetic acid, and we will then convert one-