16-2 A theoretical model of the Sun shows how energy gets from its center to its surface
 While thermonuclear fusion is the source of the Sun’s energy, this process cannot take place everywhere within the Sun. As we have seen, extremely high temperatures—in excess of 107 K—are required for atomic nuclei to fuse together to form larger nuclei. The temperature of the Sun’s visible surface, about 5800 K, is too low for these reactions to occur there. Hence, thermonuclear fusion can be taking place only within the Sun’s interior. But precisely where does it take place? And how does the energy produced by fusion make its way to the surface, where it is emitted into space in the form of photons?
While thermonuclear fusion is the source of the Sun’s energy, this process cannot take place everywhere within the Sun. As we have seen, extremely high temperatures—in excess of 107 K—are required for atomic nuclei to fuse together to form larger nuclei. The temperature of the Sun’s visible surface, about 5800 K, is too low for these reactions to occur there. Hence, thermonuclear fusion can be taking place only within the Sun’s interior. But precisely where does it take place? And how does the energy produced by fusion make its way to the surface, where it is emitted into space in the form of photons?
To answer these questions, we must understand conditions in the Sun’s interior. Ideally, we would send an exploratory spacecraft to probe deep into the Sun; in practice, the Sun’s intense heat would vaporize even the sturdiest spacecraft. Instead, astronomers use the laws of physics to construct a theoretical model of the Sun, and then compare predictions of the model to a variety of observations. (We discussed the use of models in science in Section 1-1.) Let’s see what ingredients go into building a model of this kind.
Hydrostatic Equilibrium
Note first that the Sun is not undergoing any dramatic changes. The Sun is not exploding or collapsing, nor is it significantly heating or cooling. The Sun is thus said to be in both hydrostatic equilibrium and thermal equilibrium.
To understand what is meant by hydrostatic equilibrium, imagine a slab of material in the solar interior (Figure 16-2a). In equilibrium, the slab on average will move neither up nor down. (In fact, there are upward and downward motions of material inside the Sun, but these motions average out.) Equilibrium is maintained by a balance among three forces that act on this slab:
- The downward pressure of the layers of solar material above the slab.
- The upward pressure of the hot gases beneath the slab.
- The slab’s weight—that is, the downward gravitational pull it feels from the rest of the Sun.

The pressure from below must balance both the slab’s weight and the pressure from above. Hence, the pressure below the slab must be greater than that above the slab. In other words, pressure has to increase with increasing depth. For the same reason, pressure increases as you dive deeper into the ocean (Figure 16-2b) or as you move toward lower altitudes in our atmosphere.
ANALOGY
If you had to join a vertical stack of 10 students piled on top of each other, you would naturally prefer to be on the top. Each student lower in the stack must bear the weight of all the students above them, so the pressure on each body increases with depth.
Hydrostatic equilibrium also tells us about the density of the slab of solar material. If the slab is too dense, its weight will be too large and it will sink; if the density is too low, the slab will rise. To prevent this, the density of solar material must have a certain value at each depth within the solar interior. (The same principle applies to objects that float beneath the surface of the ocean. Scuba divers wear weight belts and inflatable vests to adjust their average density so that they will neither rise nor sink but will stay submerged at the same level.)
Thermal Equilibrium
Another consideration is that the Sun’s interior is so hot that it is completely gaseous. Gases compress and become more dense when you apply greater pressure to them, so density must increase along with pressure as you go to greater depths within the Sun. Furthermore, when you compress a gas, its temperature tends to increase, so the temperature must also increase as you move toward the Sun’s center.
While the temperature in the solar interior is different at different depths, the temperature at each depth remains constant in time. This principle is called thermal equilibrium. For the Sun to be in thermal equilibrium, all the energy generated by thermonuclear reactions in the Sun’s core must be transported to the Sun’s glowing surface, where it can be radiated into space. If too much energy flowed from the core to the surface to be radiated away, the Sun’s interior would cool down; alternatively, the Sun’s interior would heat up if too little energy flowed to the surface.
CONCEPT CHECK 16-5
If our Sun were much less massive, how would the pressure at the Sun’s center be different from what it actually is?
Because pressure in the Sun’s core is due to the downward pushing weight of the overlying mass of material, having less mass pressing down would result in a lower pressure at the core.
Transporting Energy Outward from the Sun’s Core
But exactly how is energy transported from the Sun’s center to its surface? There are three methods of energy transport: conduction, convection, and radiative diffusion. Only the last two are important inside the Sun.
If you heat one end of a metal bar with a blowtorch, energy flows to the other end of the bar so that it too becomes warm. The efficiency of this method of energy transport, called conduction, varies significantly from one substance to another. For example, metal is a good conductor of heat, but plastic is not (which is why metal cooking pots often have plastic handles). Conduction is not an efficient means of energy transport in substances with low average densities, including the gases inside stars like the Sun.
Inside stars like our Sun, energy moves from center to surface by two other means: convection and radiative diffusion. Convection is the circulation of fluids—gases or liquids—between hot and cool regions. Hot gases (with lower density) rise toward a star’s surface, while cool gases (with higher density) sink back down toward the star’s center. This physical movement of gases transports heat energy outward in a star, just as the physical movement of water boiling in a pot transports energy from the bottom of the pot (where the heat is applied) to the cooler water at the surface.
In radiative diffusion, photons created in the thermonuclear inferno at a star’s center diffuse outward toward the star’s surface. Individual photons are absorbed and reemitted by atoms and electrons inside the star. The overall result is an outward migration from the hot core, where photons are constantly created, toward the cooler surface, where they escape into space.
CONCEPT CHECK 16-6
Why is the energy transport process of conduction relatively unimportant when studying how energy moves toward the Sun’s surface?
The energy transport process of conduction occurs when energy moves through a relatively dense material by hot material transferring its kinetic energy to cooler material through direct contact. The Sun’s density is simply too low for conduction to be an important process in transferring energy from one part of the Sun to another part.
Modeling the Sun
To construct a model of a star like the Sun, astrophysicists express the ideas of hydrostatic equilibrium, thermal equilibrium, and energy transport as a set of equations. To ensure that the model applies to the particular star under study, they also make use of astronomical observations of the star’s surface. (For example, to construct a model of the Sun, they use the data that the Sun’s surface temperature is 5800 K, its luminosity is 3.9 × 1026 watts, and the gas pressure and density at the surface are almost zero.) The astrophysicists then use a computer to solve their set of equations and calculate conditions layer by layer in toward the star’s center. The result is a model of how temperature, pressure, and density increase with increasing depth below the star’s surface (see Figure 9-5).
Table 16-2 and Figure 16-3 show a theoretical model of the Sun that was calculated in just this way. Different models of the Sun use slightly different assumptions, but all models give essentially the same results as those shown here. From such computer models we have learned that at the Sun’s center the density is 160,000 kg/m3 (14 times the density of lead!), the temperature is 1.55 × 107 K, and the pressure is 3.4 × 1011 atm. (One atmosphere, or 1 atm, is the average atmospheric pressure at sea level on Earth.)
| Distance from the Sun’s center (solar radii) | Fraction of luminosity | Fraction of of mass | Temperature (× 106 K) | Density (kg/m3) | Pressure relative to pressure at center |
|---|---|---|---|---|---|
| 0.0 | 0.00 | 0.00 | 15.5 | 160,000 | 1.00 |
| 0.1 | 0.42 | 0.07 | 13.0 | 90,000 | 0.46 |
| 0.2 | 0.94 | 0.35 | 9.5 | 40,000 | 0.15 |
| 0.3 | 1.00 | 0.64 | 6.7 | 13,000 | 0.04 |
| 0.4 | 1.00 | 0.85 | 4.8 | 4,000 | 0.007 |
| 0.5 | 1.00 | 0.94 | 3.4 | 1,000 | 0.001 |
| 0.6 | 1.00 | 0.98 | 2.2 | 400 | 0.0003 |
| 0.7 | 1.00 | 0.99 | 1.2 | 80 | 4 × 10−5 |
| 0.8 | 1.00 | 1.00 | 0.7 | 20 | 5 × 10−6 |
| 0.9 | 1.00 | 1.00 | 0.3 | 2 | 3 × 10−7 |
| 1.0 | 1.00 | 1.00 | 0.006 | 0.00030 | 4 × 10−13 |
| Note: The distance from the Sun’s center is expressed as a fraction of the Sun’s radius (R⊙). Thus, 0.0 is at the center of the Sun and 1.0 is at the surface. The fraction of luminosity is that portion of the Sun’s total luminosity produced within each distance from the center; this is equal to 1.00 for distances of 0.25 R⊙ or more, which means that all of the Sun’s nuclear reactions occur within 0.25 solar radius from the Sun’s center. The fraction of mass is that portion of the Sun’s total mass lying within each distance from the Sun’s center. The pressure is expressed as a fraction of the pressure at the center of the Sun. | |||||
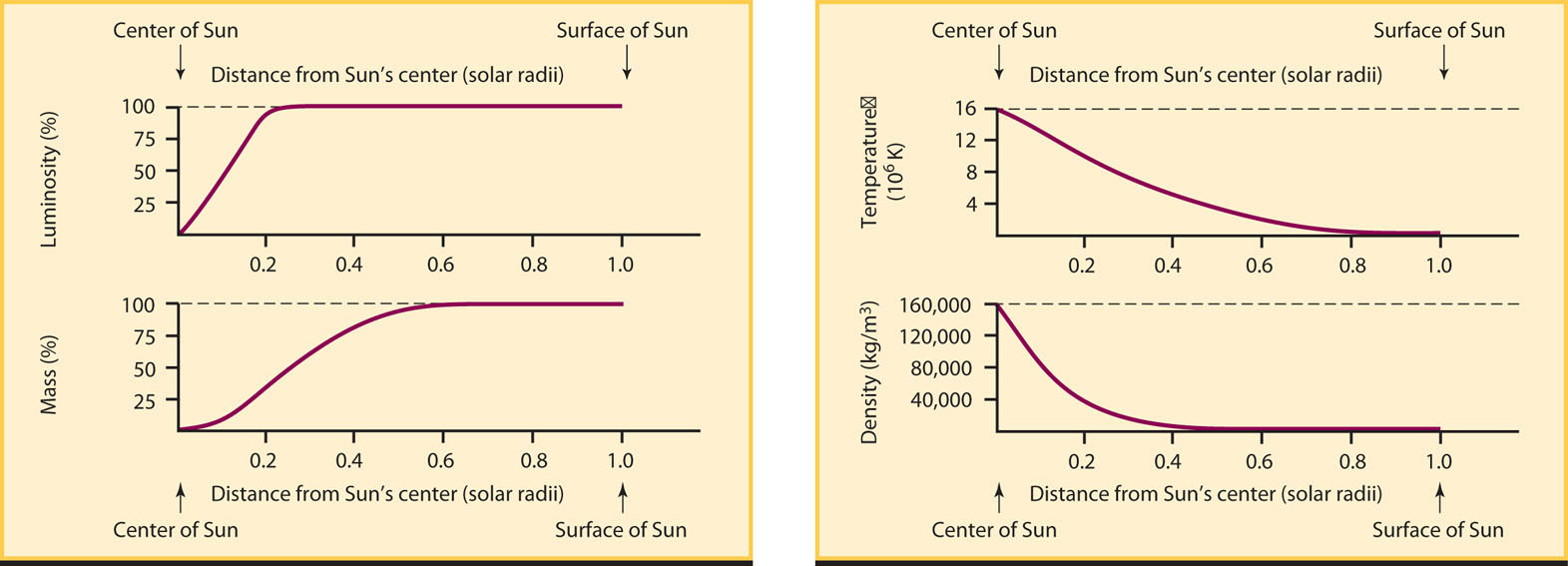
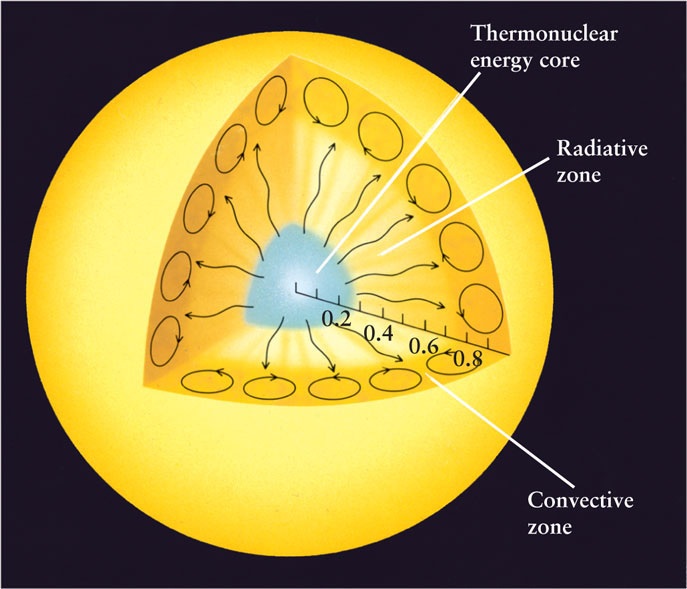
Table 16-2 and Figure 16-3 show that the solar luminosity rises to 100% at about one-quarter of the way from the Sun’s center to its surface. In other words, the Sun’s energy production occurs within a volume that extends out only to 0.25 R⊙. (The symbol R⊙ denotes the solar radius, or radius of the Sun as a whole, equal to 696,000 km.) Outside 0.25 R⊙, the density and temperature are too low for thermonuclear reactions to take place. Also note that 94% of the total mass of the Sun is found within the inner 0.5 R⊙. Hence, the outer 0.5 R⊙ contains only a relatively small amount of material.
How energy flows from the Sun’s center toward its surface depends on how easily photons move through the gas. If the solar gases are relatively transparent, photons can travel moderate distances before being scattered or absorbed, and energy is thus transported by radiative diffusion. You can think of radiative diffusion as the “free flight” of photons, and the energy is transported in these photons. If the gases are relatively opaque, photons are frequently scattered or absorbed and cannot easily get through the gas. In an opaque gas, heat builds up and convection then becomes the most efficient means of energy transport. In convection, the energy is in the form of heat; the movement of hot gas transports the energy. The gases start to churn, with hot lower-density gas moving outward and cooler gas sinking inward.
From the center of the Sun out to about 0.71 R⊙, energy is transported by radiative diffusion. Hence, this region is called the radiative zone. Beyond about 0.71 R⊙, the temperature is low enough (a mere 2 × 106 K or so) for electrons and hydrogen nuclei to join into hydrogen atoms. These atoms are very effective at absorbing photons, much more so than free electrons or nuclei, and this absorption chokes off the outward flow of photons. Therefore, beyond about 0.71 R⊙, radiative diffusion is not an effective way to transport energy. Instead, convection dominates the energy flow in this outer region, which is why it is called the convective zone. Figure 16-4 shows these aspects of the Sun’s internal structure.
The sunlight that reaches Earth today results from thermonuclear reactions that took place about 170,000 years ago
Although energy travels through the radiative zone in the form of photons, the photons have a difficult time of it. Table 16-2 shows that the material in this zone is extremely dense, so photons from the Sun’s core take a long time to diffuse through the radiative zone. As a result, it takes approximately 170,000 years for energy created at the Sun’s center to travel 696,000 km to the solar surface and finally escape as sunlight. The energy flows outward at an average rate of 50 cm per hour, or about 20 times slower than a snail’s pace.
Once the energy works its way out of the Sun, it travels much faster—at the speed of light! Thus, solar energy that reaches you today took only 8 minutes to travel the 150 million km from the Sun’s surface to Earth. But this energy was actually produced by thermonuclear reactions that took place in the Sun’s core hundreds of thousands of years ago.
CONCEPT CHECK 16-7
Which of the following decreases when we move from the Sun’s central core toward its surface: temperature or luminosity?
Only the temperature decreases with increasing distance from the Sun’s central core.
CALCULATION CHECK 16-2
By how much (in percent) does the Sun‘s temperature drop from its temperature at the central core to its temperature at 0.5 R⊙?
According to Figure 16-3, the Sun’s core temperature is about 16 million Kelvins. At a distance of 50% of the Sun’s radius, the Sun’s temperature has dropped to 4 million Kelvins, which is a drop of about 75%.