1-6 Powers-of-ten notation is a useful shorthand system for writing numbers
Learning powers-of-ten notation will help you deal with very large and very small numbers
Astronomy is a subject of extremes. Astronomers investigate the largest structures in the universe, including galaxies and clusters of galaxies. But they must also study atoms and atomic nuclei, among the smallest objects in the universe, in order to explain how and why stars shine. They also study conditions ranging from the incredibly hot and dense centers of stars to the frigid near-vacuum of interstellar space. To describe such a wide range of phenomena, we need an equally wide range of both large and small numbers.
BOX 1-1 TOOLS OF THE ASTRONOMER’S TRADE
The Small-Angle Formula
You can estimate the angular sizes of objects in the sky with your hand and fingers (see Figure 1-12). Using rather more sophisticated equipment, astronomers can measure angular sizes to a fraction of an arcsecond. Keep in mind, however, that angular size is not the same as actual size. As an example, if you extend your arm while looking at a full moon, you can completely cover the Moon with your thumb. That’s because from your perspective, your thumb has a larger angular size (that is, it subtends a larger angle) than the Moon. But the actual size of your thumb (about 2 centimeters) is much less than the actual diameter of the Moon (more than 3000 kilometers).
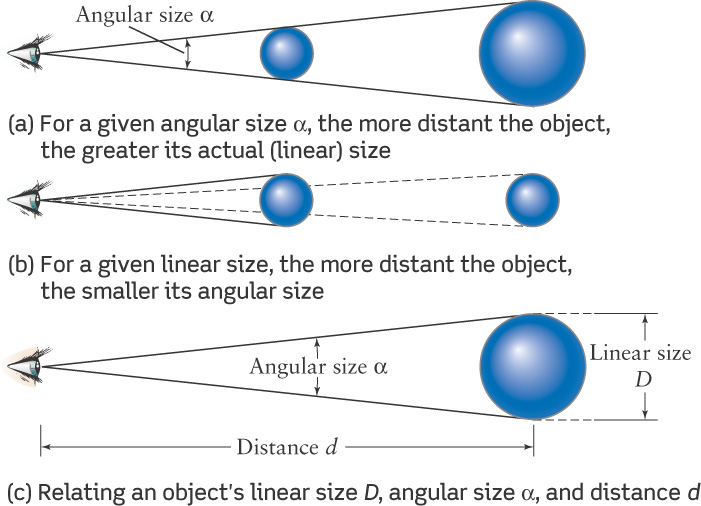
The accompanying figure shows how the angular size of an object is related to its linear size. Part (a) of the figure shows that for a given angular size, the more distant the object, the larger its actual size. For example, your fingertip held at arm’s length covers the full moon, but the Moon is much farther away and is far larger in linear size. Part (b) shows that for a given linear size, the angular size decreases the farther away the object. This is why a car looks smaller and smaller as it drives away from you.
We can put these relationships together into a single mathematical expression called the small-angle formula. Suppose that an object subtends an angle a (the Greek letter alpha) and is at a distance d from the observer, as in part (c) of the figure. If the angle a is small, as is almost always the case for objects in the sky, the width or linear size (D) of the object is given by the following expression:
The small-angle formula
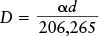

The number 206,265 is required in the formula so that the units of a are in arcseconds. (206,265 is the number of arcseconds in a complete 360° circle divided by the number 2p.) As long as the same units are used for D and d, any units for linear distance can be used (km, light-years, etc.).
The following examples show two different ways to use the small-angle formula. In both examples we follow a four-step process: Evaluate the situation given in the example, decide which tools are needed to solve the problem, use those tools to find the answer to the problem, and review the result to see what it tells you. Throughout this book, we’ll use these same four steps in all examples that require the use of formulas. We encourage you to follow this four-step process when solving problems for homework or exams. You can remember these steps by their acronym: S.T.A.R.
EXAMPLE: On December 11, 2006, Jupiter was 944 million kilometers from Earth and had an angular diameter of 31.2 arcsec. From this information, calculate the actual diameter of Jupiter in kilometers.
Situation: The astronomical object in this example is Jupiter, and we are given its distance d and its angular size a (the same as angular diameter). Our goal is to find Jupiter’s diameter D.
Tools: The equation to use is the small-angle formula, which relates the quantities d, a, and D. Note that when using this formula, the angular size a must be expressed in arcseconds.
Answer: The small-angle formula as given is an equation for D. Plugging in the given values a = 31.2 arcsec and d = 944 million kilometers,

Because the distance d to Jupiter is given in kilometers, the diameter D is also in kilometers.
Review: Does our answer make sense? From Appendix 2 at the back of this book, the equatorial diameter of Jupiter measured by spacecraft flybys is 142,984 kilometers, so our calculated answer is very close.
EXAMPLE: Under excellent conditions, a telescope on Earth can see details with an angular size as small as 1 arcsec. What is the greatest distance at which you could see details as small as 1.7 meters (the height of a typical person) under these conditions?
Situation: Now the object in question is a person, whose linear size D we are given. Our goal is to find the distance d at which the person has an angular size a equal to 1 arcsec.
Tools: Again we use the small-angle formula to relate d, a, and D.
Answer: We first rewrite the formula to solve for the distance d, then plug in the given values D = 1.7 m and a = 1 arcsec:
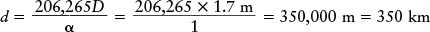
Review: This value is much less than the distance to the Moon, which is 384,000 kilometers. Thus, even the best telescope on Earth could not be used to see an astronaut walking on the surface of the Moon.
Powers-of-Ten Notation: Large Numbers
Astronomers avoid such confusing terms as “a million billion billion” by using a standard shorthand system called powers-of-ten notation. All the cumbersome zeros that accompany a large number are consolidated into one term consisting of 10 followed by an exponent, which is written as a superscript. The exponent indicates how many zeros you would need to write out the long form of the number. Thus,

and so forth. The exponent also tells you how many tens must be multiplied together to give the desired number, which is why the exponent is also called the power of ten. For example, ten thousand can be written as 104 (“ten to the fourth” or “ten to the fourth power”) because 104 = 10 × 10 × 10 × 10 = 10,000.
In powers-of-ten notation, numbers are written as a figure between 1 and 10 multiplied by the appropriate power of ten. The approximate distance between Earth and the Sun, for example, can be written as 1.5 × 108 kilometers (or 1.5 × 108 km, for short). Once you get used to it, this is more convenient than writing “150,000,000 kilometers” or “one hundred and fifty million kilometers.” (The same number could also be written as 15 × 107 or 0.15 × 109, but the preferred form is always to have the first figure be between 1 and 10.)
Calculators and Powers-of-Ten Notation
Most electronic calculators use a shorthand for powers-of-ten notation. To enter the number 1.5 × 108, you first enter 1.5, then press a key labeled “EXP” or “EE,” then enter the exponent 8. (The EXP or EE key takes care of the “× 10” part of the expression.) The number will then appear on your calculator’s display as “1.5 E 8,” “1.5 8,” or some variation of this; typically the “× 10” is not displayed as such. There are some variations from one kind of calculator to another, so you should spend a few minutes reading over your calculator’s instruction manual to make sure you know the correct procedure for working with numbers in powers-of-ten notation. You will be using this notation continually in your study of astronomy, so this is time well spent.
CAUTION!
Confusion can result from the way that calculators display powers-of-ten notation. Since 1.5 × 108 is displayed as 1.5 8 or 1.5 E 8, it is not uncommon to think that 1.5 × 108 is the same as 1.58. That is not correct, however; 1.58 is equal to 1.5 multiplied by itself 8 times, or 25.63, which is not even close to 150,000,000 = 1.5 × 108. Another, not uncommon, mistake is to write 1.5 × 108 as 158. If you are inclined to do this, perhaps you are thinking that you can multiply 1.5 by 10, then tack on the exponent later. Another process that does not work: 158 is equal to 15 multiplied by itself 8 times, or 2,562,890,625, which again is nowhere near 1.5 × 108. Reading over the manual for your calculator will help you to avoid these common errors.
Powers-of-Ten Notation: Small Numbers
You can use powers-of-ten notation for numbers that are less than one by using a minus sign in front of the exponent. A negative exponent tells you to divide by the appropriate number of tens. For example, 10-2 (“ten to the minus two”) means to divide by 10 twice, so 10-2 = 1/10 × 1/10 = 1/100 = 0.01. This same idea tells us how to interpret other negative powers of ten:
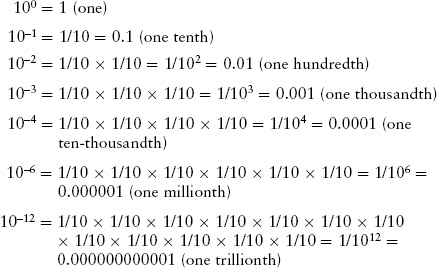
and so forth.
As these examples show, negative exponents tell you how many tenths must be multiplied together to give the desired number. For example, one ten-thousandth, or 0.0001, can be written as 10-4 (“ten to the minus four”) because 10-4 = 1/10 × 1/10 × 1/10 × 1/10 = 0.0001.
A useful shortcut in converting a decimal to powers-of-ten notation is to notice where the decimal point is. For example, the decimal point in 0.0001 is four places to the left of the “1,” so the exponent is -4, that is, 0.0001 = 10-4.
You can also use powers-of-ten notation to express a number like 0.00245, which is not a multiple of 1/10. For example, 0.00245 = 2.45 × 0.001 = 2.45 × 10-3. (Again, the standard for powers-of-ten notation is that the first figure is a number between 1 and 10.) This notation is particularly useful when dealing with very small numbers. A good example is the diameter of a hydrogen atom, which is much more convenient to state in powers-of-ten notation (1.1 × 10-10 meter, or 1.1 × 10-10 m) than as a decimal (0.00000000011 m) or a fraction (110 trillionths of a meter.)
Because it bypasses all the awkward zeros, powers-of-ten notation is ideal for describing the size of objects as small as atoms or as big as galaxies (Figure 1-13). Box 1-2 explains how powers-of-ten notation also makes it easy to multiply and divide numbers that are very large or very small.

BOX 1-2 TOOLS OF THE ASTRONOMER’S TRADE
Arithmetic with Powers-of-Ten Notation
Using powers-of-ten notation makes it easy to multiply numbers. For example, suppose you want to multiply 100 by 1000. If you use ordinary notation, you have to write a lot of zeros:
100 × 1000 = 100,000 (one hundred thousand)
By converting these numbers to powers-of-ten notation, we can write this same multiplication more compactly as
102 × 103 = 105
Because 2 + 3 = 5, we are led to the following general rule for multiplying numbers expressed in terms of powers of ten: Simply add the exponents.
EXAMPLE: 104 × 103 = 104+3 = 107.
To divide numbers expressed in terms of powers of ten, remember that 10-1 = 1/10, 10-2 = 1/100, and so on. The general rule for any exponent n is

In other words, dividing by 10n is the same as multiplying by 10-n. To carry out a division, you first transform it into multiplication by changing the sign of the exponent, and then carry out the multiplication by adding the exponents.
EXAMPLE: 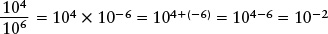
Usually a computation involves numbers like 3.0 × 1010, that is, an ordinary number multiplied by a factor of 10 with an exponent. In such cases, to perform multiplication or division, you can treat the numbers separately from the factors of 10n.
EXAMPLE: We can redo the first numerical example from Box 1-1 in a straightforward manner by using exponents:
