21-2 The general theory of relativity predicts black holes
 Einstein’s special theory of relativity is a special case in the sense that it does not include the effects of gravity. Einstein’s next goal was to develop an even more comprehensive theory that includes gravity and its effects on space and time. This is Einstein’s general theory of relativity, which he published in 1915.
Einstein’s special theory of relativity is a special case in the sense that it does not include the effects of gravity. Einstein’s next goal was to develop an even more comprehensive theory that includes gravity and its effects on space and time. This is Einstein’s general theory of relativity, which he published in 1915.
In the special theory of relativity, a relative velocity between observers leads to different observations of distance and time. In addition to all of the effects of the special theory, the general theory of relativity describes how observers in gravitational fields of different strengths also measure differences in distance and time.
The Equivalence Principle
According to Newton’s theory of gravity, an apple falls to the floor because the force of gravity pulls the apple down. But Einstein pointed out that the apple would appear to behave in exactly the same way in space, far from the gravitational influence of any planet or star, if the floor were to accelerate upward (in other words, if the floor came up to meet the apple).
In Figure 21-3, two famous gentlemen are watching an apple fall toward the floor of their closed compartments. They have no way of telling who is at rest on Earth and who is in the hypothetical elevator moving upward through empty space at a constantly increasing speed. This is an example of Einstein’s equivalence principle, which states that in a small volume of space, the downward pull of gravity can be accurately and completely duplicated by an upward acceleration of the observer.
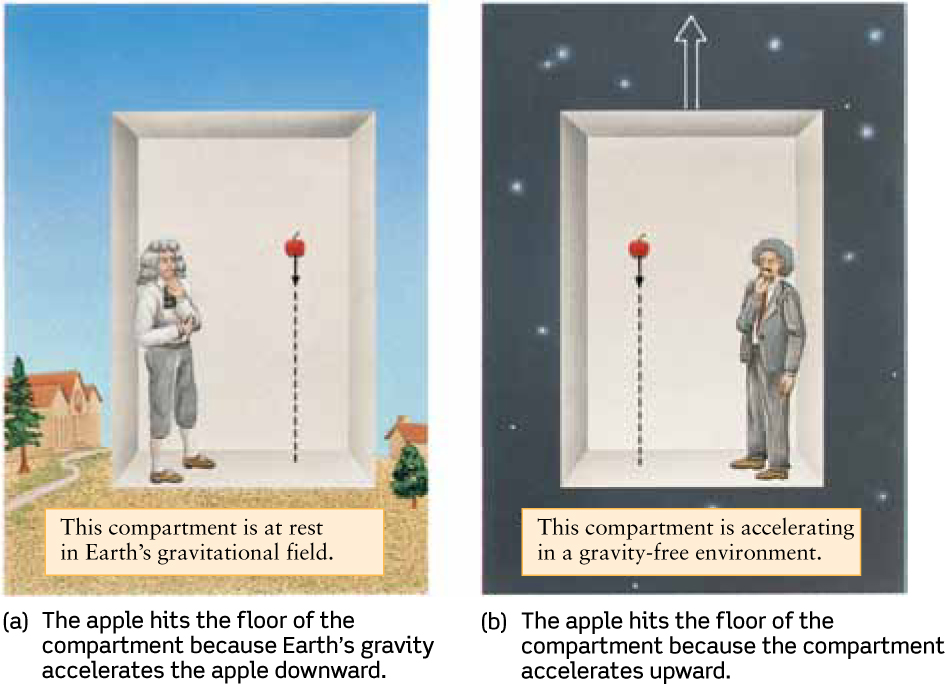
 The Equivalence Principle The equivalence principle asserts that you cannot distinguish between (a) being at rest in a gravitational field and (b) being accelerated upward in a gravity-free environment. This idea was an important step in Einstein’s quest to develop the general theory of relativity.
The Equivalence Principle The equivalence principle asserts that you cannot distinguish between (a) being at rest in a gravitational field and (b) being accelerated upward in a gravity-free environment. This idea was an important step in Einstein’s quest to develop the general theory of relativity.
The equivalence principle is the key to the general theory of relativity. It allowed Einstein to focus entirely on motion, rather than force, in discussing gravity. A hallmark of gravity is that it causes the same acceleration no matter the mass of the object. For example, a baseball and a cannon ball have very different masses, but if you drop them side by side in a vacuum, they accelerate downward at exactly the same rate. To explain this observation, Einstein envisioned gravity as being caused by a curvature of space. In fact, his general theory of relativity describes gravity entirely in terms of the geometry of both space and time, that is, of spacetime. Far from a source of gravity, like a planet or a star, spacetime is “flat” and clocks tick at their normal rate. Closer to a source of gravity, however, space is curved and clocks slow down.
ANALOGY
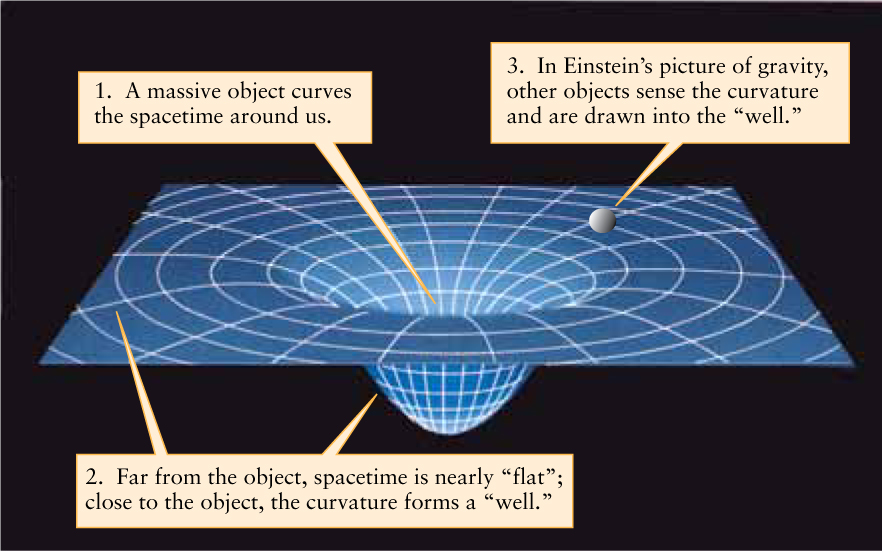
A useful analogy is to picture the spacetime near a massive object such as the Sun as being curved like the surface in Figure 21-4. Imagine a ball rolling along this surface. Far from the “well” that represents the Sun, the surface is fairly flat and the ball moves in a straight line. If the ball passes near the well, however, it curves in toward it. If the ball is moving at an appropriate speed, it might move in an orbit around the sides of the well. The curvature of the well has the same effect on a ball of any size, which explains why gravity produces the same acceleration on objects of different mass.
Testing the General Theory
Einstein’s general theory of relativity and its picture of curved spacetime have been tested in a variety of different ways. In what follows, we discuss some key experimental tests of the theory.
Careful experiments have verified the key ideas of Einstein’s theory of gravity
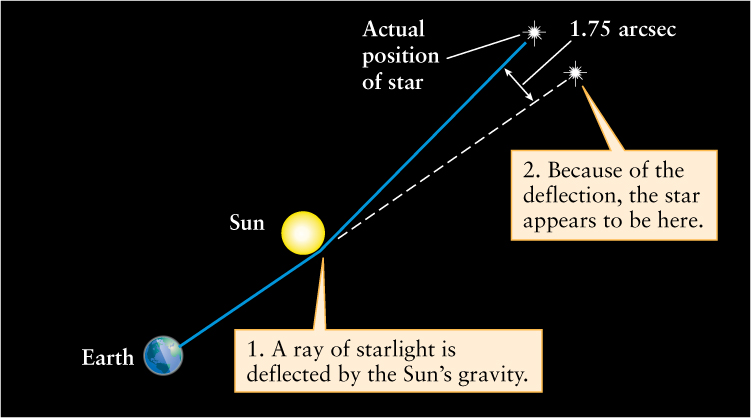
Experimental Test 1: The gravitational bending of light. Light rays naturally travel in straight lines. But if the space through which the rays travel is curved, as happens when light passes near the surface of a massive object like the Sun, the paths of the rays will likewise be curved (Figure 21-5). In other words, gravity should bend light rays. This prediction was first tested in 1919 during a total solar eclipse. During totality, when the Moon blocked out the Sun’s disk, astronomers photographed the stars around the Sun. Careful measurements afterward revealed that the stars around the Sun were shifted from their usual positions by an amount consistent with Einstein’s theory.
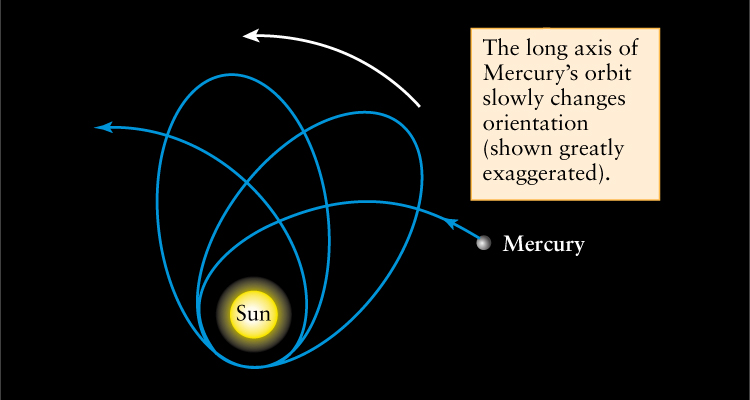
Experimental Test 2: The precession of Mercury’s orbit. As the planet Mercury moves along its elliptical orbit, the orbit itself slowly changes orientation, or precesses (Figure 21-6). Most of Mercury’s precession is caused by the gravitational pull of the other planets, as explained by Newtonian mechanics. But once the effects of all the other planets had been accounted for, there remained an unexplained excess rotation of Mercury’s major axis of 43 arcsec per century. Although this discrepancy may seem very small, it frustrated astronomers for half a century. Some astronomers searched for a missing planet even closer to the Sun that might be tugging on Mercury; none has ever been found. Einstein showed that at Mercury’s position close to the Sun, the general theory of relativity predicts a small correction to Newton’s description of gravity. This correction is just enough to account for the excess precession.
Experimental Test 3: The gravitational slowing of time and the gravitational red shift (Figure 21-7). In the general theory of relativity, a massive object such as Earth warps time as well as space. Einstein predicted that clocks on the ground floor of a building should tick slightly more slowly than clocks on the top floor, which are farther from Earth (Figure 21-7a).
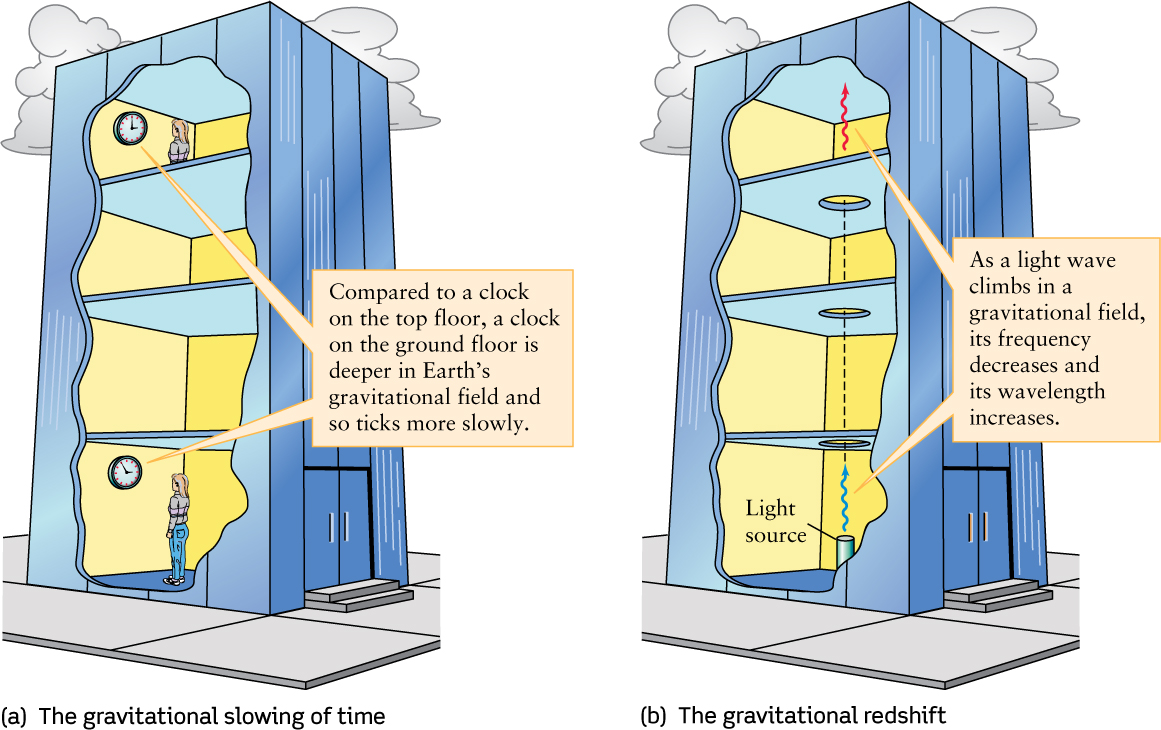
A light wave can be thought of as a clock; just as a clock makes a steady number of ticks per minute, an observer sees a steady number of complete cycles of a light wave passing by each second. If a light beam is aimed straight up from the ground floor of a building, an observer at the top floor will measure a “slow-ticking” light wave with a lower frequency, and thus a longer wavelength, than will an observer on the ground floor (Figure 21-7b). Because photons with longer wavelengths have lower energy, the increase in wavelength means that a photon reaching the top floor has less energy than when it left the ground floor. (You may want to review the discussion of frequency and wavelength in Section 5-2 as well as the description of photons in Section 5-5.) These effects, which have no counterpart in Newton’s theory of gravity, are called the gravitational redshift.
CAUTION!
Be careful not to confuse the gravitational redshift with a Doppler shift. In the Doppler effect, redshifts are caused by a light source moving away from an observer. Gravitational redshifts, by contrast, are caused by time flowing at different rates at different locations. No motion is involved.
The American physicists Robert Pound and Glen Rebka first measured the gravitational redshift in 1960 using gamma rays fired between the top and bottom of a shaft 20 m tall. Because Earth’s gravity is relatively weak, the redshift that they measured was very small (∆λ/λ = 2.5 × 10−15) but was in complete agreement with Einstein’s prediction.
Much larger shifts are seen in the spectra of white dwarfs, whose spectral lines are redshifted as light climbs out of the white dwarf’s intense surface gravity. As an example, the gravitational redshift of the spectral lines of the white dwarf Sirius B (see Figure 20-9) is ∆λ/λ = 3.0 × 10−4, which also agrees with the general theory of relativity.
 Experimental Test 4: Gravitational waves. Electric charges oscillating up and down in a radio transmitter’s antenna produce electromagnetic radiation. In a similar way, the general theory of relativity predicts that oscillating massive objects should produce gravitational radiation, or gravitational waves. (Newton’s theory of gravity makes no such prediction.)
Experimental Test 4: Gravitational waves. Electric charges oscillating up and down in a radio transmitter’s antenna produce electromagnetic radiation. In a similar way, the general theory of relativity predicts that oscillating massive objects should produce gravitational radiation, or gravitational waves. (Newton’s theory of gravity makes no such prediction.)
Gravitational radiation is exceedingly difficult to detect, because it is by nature much weaker than electromagnetic radiation. Although physicists have built a number of sensitive “antennas” for gravitational radiation, no confirmed detections have yet been made. But compelling indirect evidence for the existence of gravitational radiation has come from a binary system of two neutron stars. Russell Hulse and Joseph Taylor at the University of Massachusetts discovered that these stars are slowly spiraling toward each other and losing energy in the process. The rate at which they lose energy is just what would be expected if the two neutron stars are emitting gravitational radiation as predicted by Einstein. Hulse and Taylor shared the 1993 Nobel Prize in Physics for their discovery.
Recent Evidence for Einstein’s Gravity Theory
The curvature of spacetime was measured around Earth in 2011. Analogous to Figure 21-4, a scientific satellite called Gravity Probe B carrying sensitive gyroscopes was sent to measure the curvature produced by Earth’s gravity. Spacetime curvature would produce a subtle precession of a gyroscope’s axis as it orbits Earth, which is an effect that is unique to Einstein’s theory. Amazingly, scientists reported precise agreement between general relativity and Gravity Probe B’s detailed measurements.
Using the world’s most accurate clocks in 2010, the gravitational slowing of time has been measured at two vertical positions separated by only 1 foot in a laboratory. Just as predicted, time slows down enough that the lower clock would read about 90 billionths of a second less over a 79-year period.
Another context in which the general theory of relativity shows up is when certain technology, by its very nature, is highly sensitive. For example, global positioning system (GPS) satellites must use extremely accurate clocks in order to triangulate an accurate position on Earth. The effects of gravity slow down time on Earth’s surface, compared to the satellite’s clocks, so general relativity must be taken into account for an accurate GPS result. Without general relativity included, GPS would accumulate errors of more than 10 km per day!
The general theory of relativity has never made an incorrect prediction. It now stands as our most accurate and complete description of gravity. Einstein demonstrated that Newtonian mechanics is accurate only when applied to low speeds and weak gravity. If extremely high speeds or powerful gravity are involved, only a calculation using relativity will give correct answers. As we will see next, the bizarre phenomena of a black hole is an example of strong gravity that Newton’s theory does not describe.
CONCEPT CHECK 21-3
Suppose two identical clocks are synchronized far out in space and away from any strong sources of gravity. You learn what time they measure by radio waves sent from each clock. Then one clock is placed near a massive planet, while you stay floating in space with the other clock. After one hour has passed on the clock next to you, has more time or less time passed on the clock near the planet?
Less time has passed on the clock near the planet—the planet’s gravity slows down time; the stronger the gravity, the more time slows down.
CONCEPT CHECK 21-4
Consider the same set of clocks in ConceptCheck 21-3. When radio waves from the clock near the planet reach you out in space, are they the same wavelength as when they were emitted near the planet?
No. As the radio waves “climb” out of the gravitational field of the planet, they experience a gravitational redshift—the frequency decreases and the wavelength increases.
The Formation of Black Holes
Perhaps the most dramatic prediction of the general theory of relativity concerns what happens when a large amount of matter is concentrated in a small volume. We have seen that if a dying star is not too massive, it ends up as a white dwarf star. If the dying star is more massive than the Chandrasekhar limit of about 1.4 M⊙, it cannot exist as a stable white dwarf star and, instead, shrinks down to form a neutron star. But if the dying star has more mass than the maximum permissible for a neutron star, about 2 to 3 M⊙, not even the internal pressure of neutrons (the degenerate neutron pressure) can hold the star up against its own gravity, and the core collapses.
As the star’s core becomes compressed to enormous densities, the strength of gravity at the surface of this rapidly shrinking sphere also increases dramatically. According to the general theory of relativity, the space immediately surrounding the core becomes so highly curved that it closes on itself (Figure 21-8). Photons flying outward at an angle from such an object’s surface would arc back inward, while photons that fly straight outward undergo such a strong gravitational redshift that they lose all their energy and cease to exist.
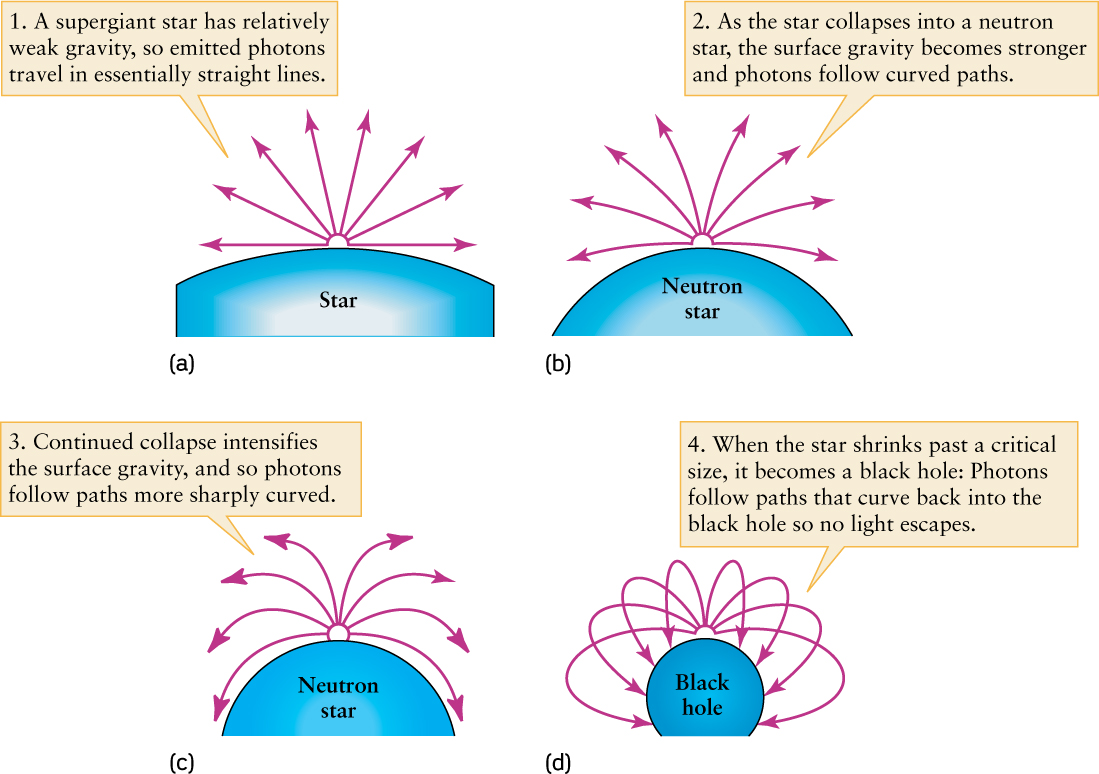
Ordinary matter can never travel as fast as light. Hence, if light cannot escape from the collapsing core, neither can anything else. An object from which neither light nor matter can escape is called a black hole. In a sense, a hole is punched in the fabric of the universe, and the dying star disappears into this cavity (Figure 21-9).
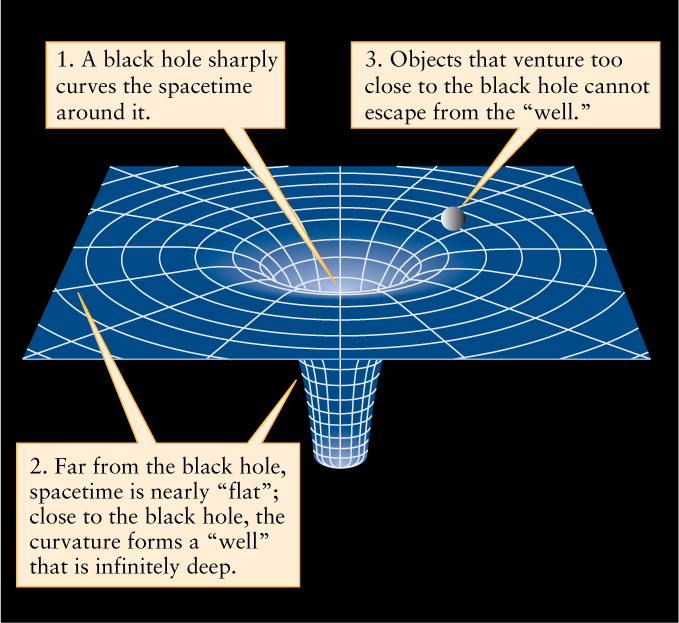
The mass of the star’s collapsing core forms the black hole; this mass gives the spacetime around the black hole its strong curvature. Thanks to this curvature, the black hole’s gravitational influence can still be felt by other objects. However, most of the original mass of the dying star does not make it into the black hole. For example, a 5-M⊙ black hole formed by core-collapse would probably come from a star of about 20 M⊙ or more.
CAUTION!
Some low-quality science-fiction movies and books suggest that black holes are evil things that go around gobbling up everything in the universe. Not so! The bizarre effects created by highly warped spacetime are limited to a region quite near the hole. For example, the effects of the general theory of relativity predominate only within 1000 km of a 10-M⊙ black hole. Beyond 1000 km, gravity is weak enough that Newtonian physics can adequately describe everything. If our own Sun somehow turned into a black hole (an event that, happily, seems to be quite impossible), the orbits of the planets would hardly be affected at all.
CONCEPT CHECK 21-5
The exact number is not known, but approximately what is the lowest-mass black hole you might expect from a stellar core collapse?
Neutron stars can support up to 2 to 3 M⊙ without collapsing further. Masses larger than this can collapse into black holes, so these are the lowest black hole masses expected from stellar core-collapse.
The Escape Speed from Black Holes is the Speed of Light
One way to understand black holes is to first consider the escape speed from a planet (see Section 4-7). The escape speed of a planet is the minimum ejection speed an object must have at the planet’s surface in order to escape the planet and never return.
Very importantly, if you imagine compressing a planet’s mass into a smaller radius, the planet’s escape speed increases. It is even possible, if an object were compressed into a small enough radius, that its calculated escape speed would exceed the speed of light. Since nothing—not even light—can travel faster than the speed of light, nothing can escape such an unusual object. An object with an escape speed exceeding the speed of light is a black hole. Surrounding the black hole, where the escape speed from the hole just equals the speed of light, is the event horizon.
You can think of the event horizon as the “surface” of the black hole, although it is just a spherical boundary and not a physical surface. Once a massive dying star collapses to within its event horizon, it disappears permanently from the universe. The term “event horizon” is quite appropriate, because this surface is like a horizon beyond which we cannot see any events.
Perhaps the most remarkable aspect of black holes is that they really exist! As we will see, astronomers have located a number of black holes with masses between about 5 and 15 M⊙. Black holes in this range (or even greater, if discovered) are called stellar-mass black holes, and they are assumed to form from the cores of supernovae. What is truly amazing is that astronomers have also discovered many enormous black holes containing millions or billions of solar masses; these were formed through a different and unknown mechanism. These discoveries are a resounding confirmation of the ideas of the general theory of relativity. In the next three sections we will see how astronomers hunt down black holes in space.
CONCEPT CHECK 21-6
Suppose that aliens could somehow add mass to our Moon without changing the Moon’s radius. Does the Moon’s escape speed increase or decrease? What happens if the Moon’s escape speed exceeds the speed of light?
If an object is compressed, its escape speed increases, and the escape speed also increases if more mass is added to the object while maintaining its size. When an object’s escape speed exceeds the speed of light, no light can escape, and the object becomes a black hole.